Скорость движения маятника формула

Формулы математического маятника

Определение и формулы математического маятника

Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

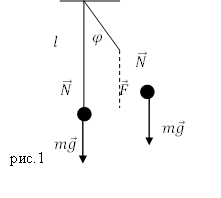
Уравнение движения математического маятника

Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $varphi (t):$

где $alpha $ — начальная фаза колебаний; $_0$ — амплитуда колебаний; $_0$ — циклическая частота.

Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса:

Период колебаний математического маятника ($T$) в этом случае равен:

Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:

Максимальное значение потенциальной энергии математического маятника равно:

Максимальная величина кинетической энергии:

где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m=_0x_m$ — максимальная скорость.

Примеры задач с решением

Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?

Решение. Сделаем рисунок.

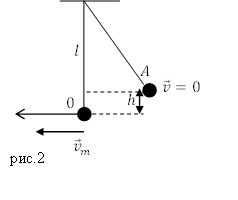
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:

Из уравнения (1.1) найдем искомую высоту:

Ответ. $h=frac<2g>$

Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit<>

Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:

Выразим из нее ускорение:

Проведем вычисления ускорения силы тяжести:

Ответ. $g=9,87 frac<�м><�с^2>$

Максимальная скорость пружинного маятника формула

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):

В этом соотношении – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

Таким образом, груз некоторой массы , прикрепленный к пружине жесткости , второй конец которой закреплен неподвижно (рис. 2.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором .

Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона:

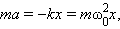
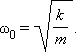
Частота называется собственной частотой колебательной системы.

Период гармонических колебаний груза на пружине равен

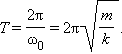
При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную

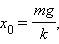
и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае.

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени :

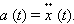
Поэтому второй закон Ньютона для груза на пружине может быть записан в виде

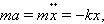
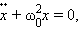
где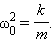

Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида

Уравнение (*) называется уравнением свободных колебаний . Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период . Такие параметры колебательного процесса, как амплитуда _m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.

Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то _m = , .

Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость 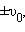то

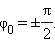
Таким образом, амплитуда _m свободных колебаний и его начальная фаза определяются начальными условиями .

Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения:

Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)

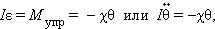
где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение.

По аналогии с грузом на пружине можно получить:

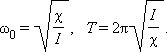
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.

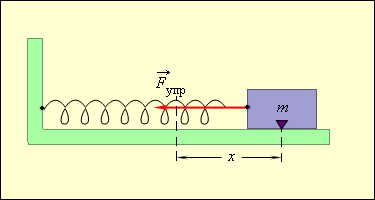
Пружинный маятник представляет собой материальную точку массой , прикрепленную к абсолютно упругой невесомой пружине с жесткостью 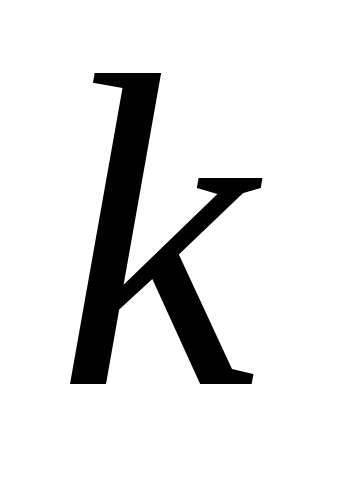. Различают два наиболее простых случая: горизонтальный (рис.15,а) и вертикальный (рис.15, б) маятники.

а) Горизонтальный маятник (рис. 15,а). При смещении груза 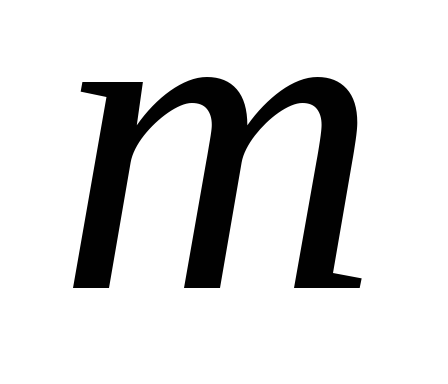из положения равновесия 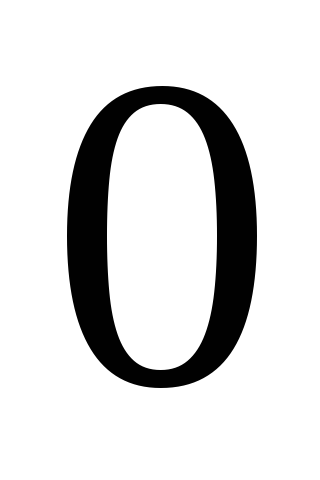на величину 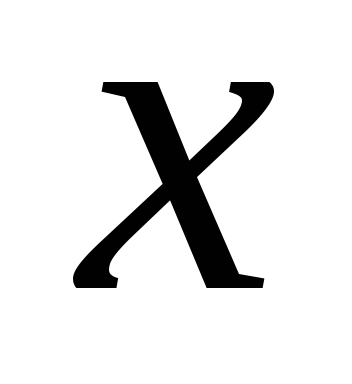на него действует в горизонтальном направлениивозвращающая упругая сила 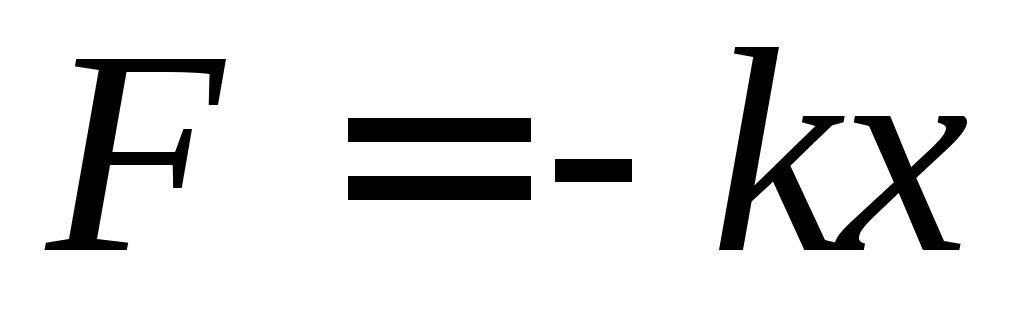(закон Гука).

Предполагается, что горизонтальная опора, по которой скользит груз 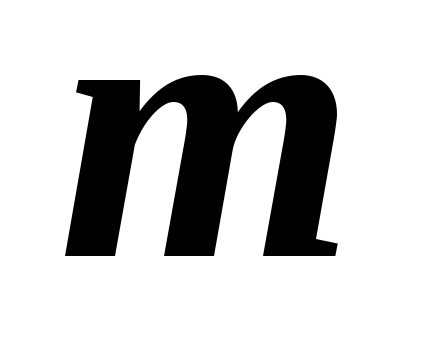при своих колебаниях, абсолютно гладкая (трения нет).

б) Вертикальный маятник (рис.15, б). Положение равновесия в этом случае характеризуется условием:

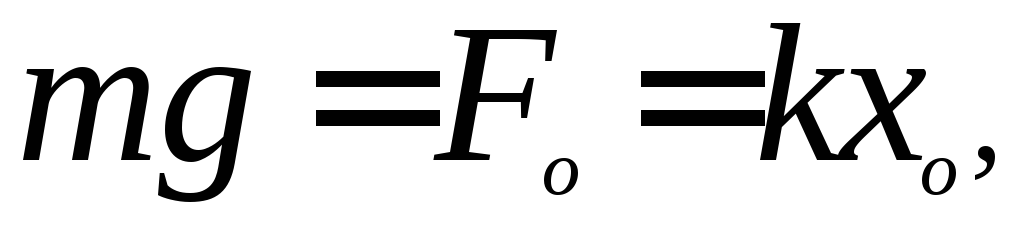
где 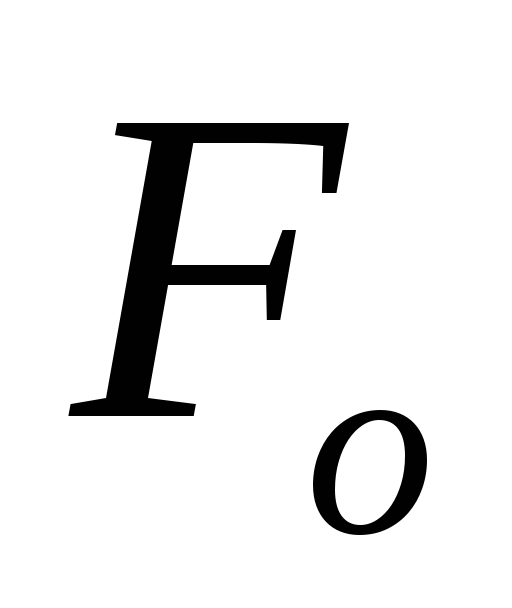— величина упругой силы, действующей на груз 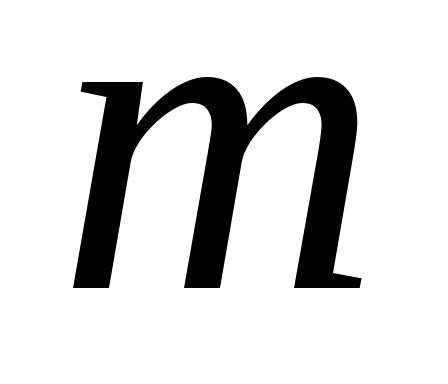при статическом растяжении пружины на 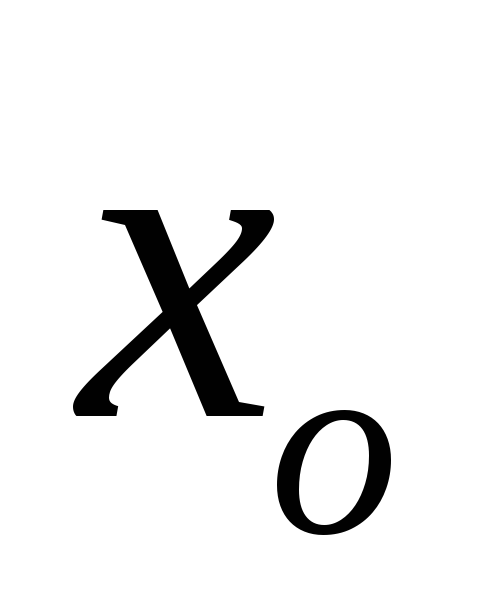под действием силы тяжести груза.

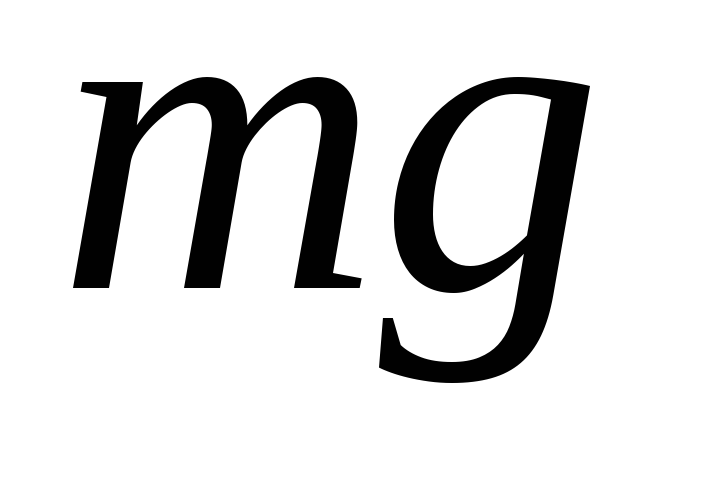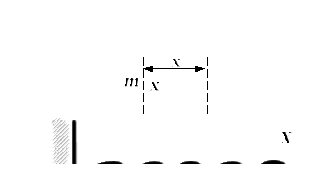
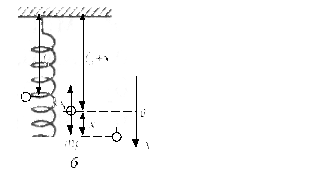
Рис.15. Пружинный маятник: а – горизонтальный и б – вертикальный

Если растянуть пружину и отпустить груз, то он начнет совершать вертикальные колебания. Если смещение в какой-то момент времени будет , то сила упругости запишется теперь как .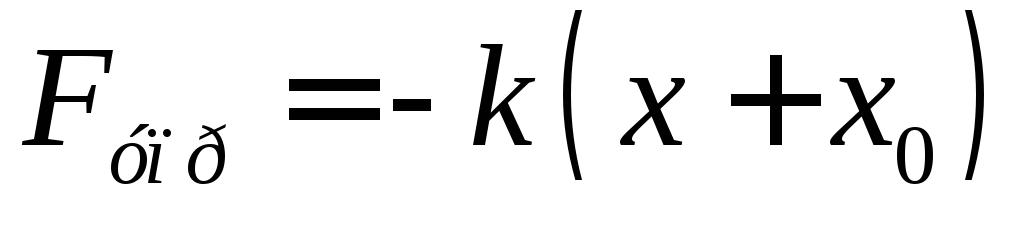

В обоих рассмотренных случаях пружинный маятник совершает гармонические колебания с периодом

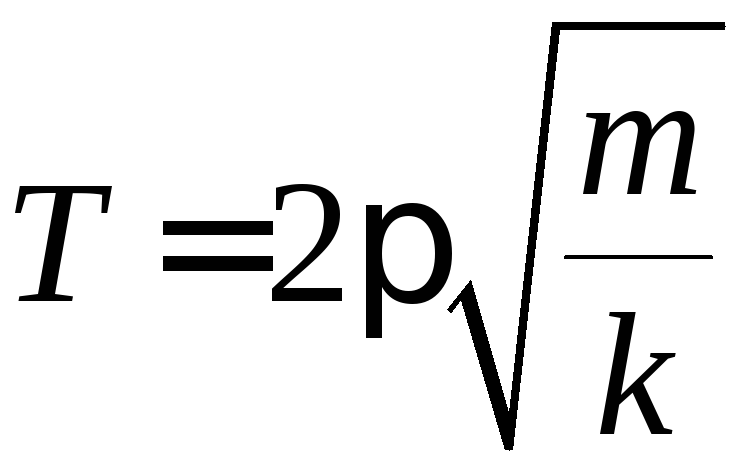(27)

и циклической частотой

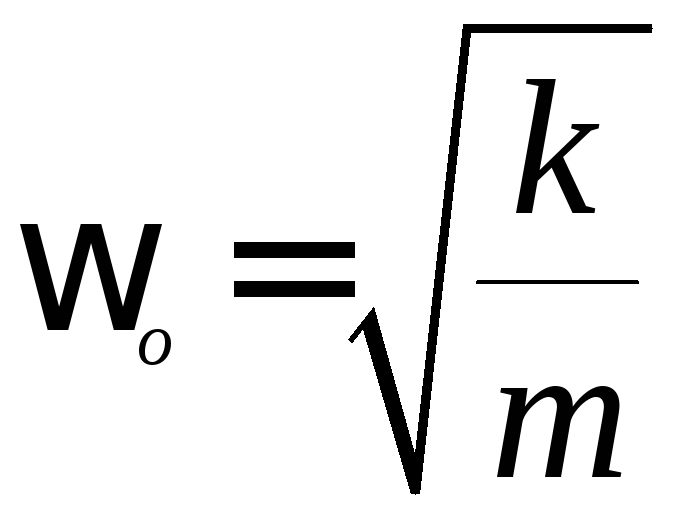_. (28)

На примере рассмотрения пружинного маятника можно сделать вывод о том, что гармонические колебания – это движение, вызванное силой, возрастающей пропорционально смещению 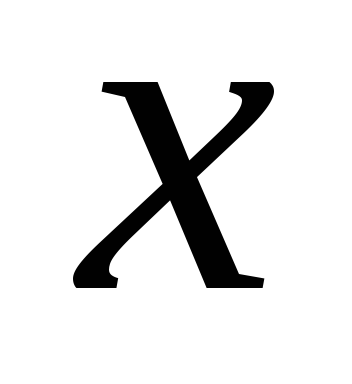. Таким образом, если возвращающая сила по виду напоминает закон Гука 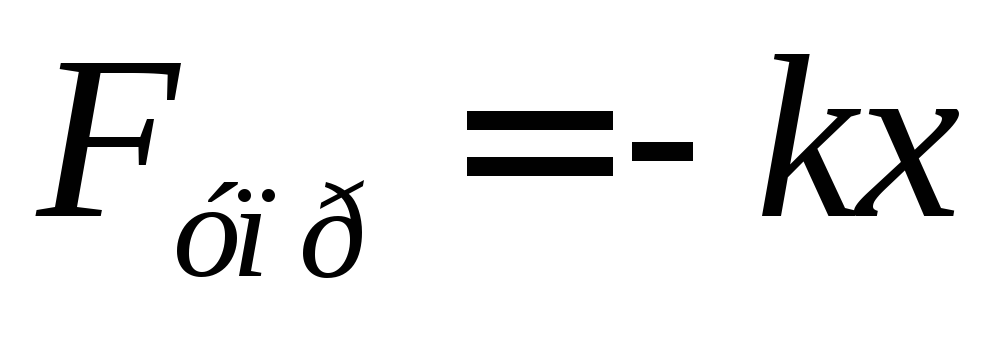(она получила название квазиупругой силы), то система должна совершать гармонические колебания. В момент прохождения положения равновесия на тело не действует возвращающая сила, однако, тело по инерции проскакивает положение равновесия и возвращающая сила меняет направление на противоположное.

Математический маятник

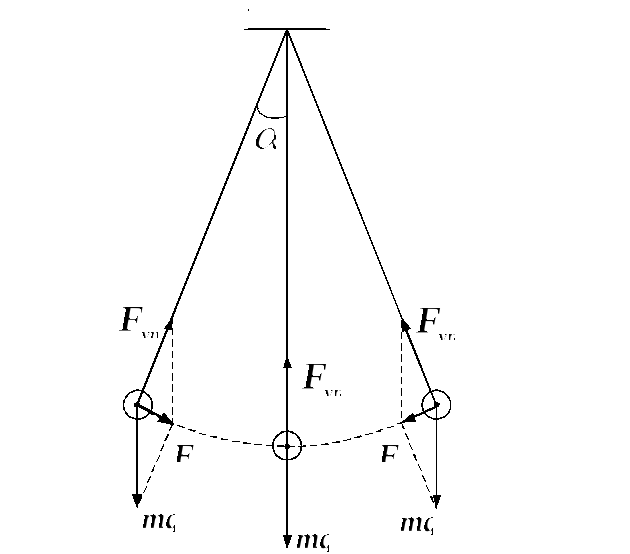
Рис.16. Математический маятник

Математический маятник представляет собой идеализированную систему в виде материальной точки, подвешенной на невесомой нерастяжимой нити длиной 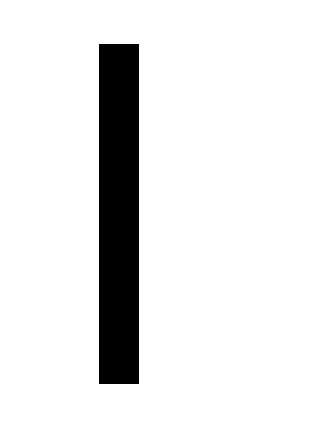, которая совершает малые колебания под действием силы тяжести (рис. 16).

Колебания такого маятника при малых углах отклонения (не превышающих 5º) можно считать гармоническими, и циклическая частота математического маятника:

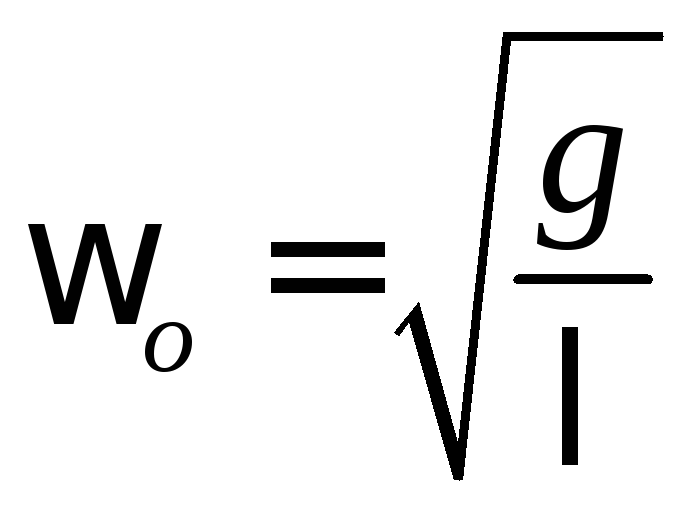, (29)

. (30)

2.3. Энергия тела при гармонических колебаниях

Энергия, сообщенная колебательной системе при начальном толчке, будет периодически преобразовываться: потенциальная энергия деформированной пружины будет переходить в кинетическую энергию движущегося груза и обратно.

Пусть пружинный маятник совершает гармонические колебания с начальной фазой 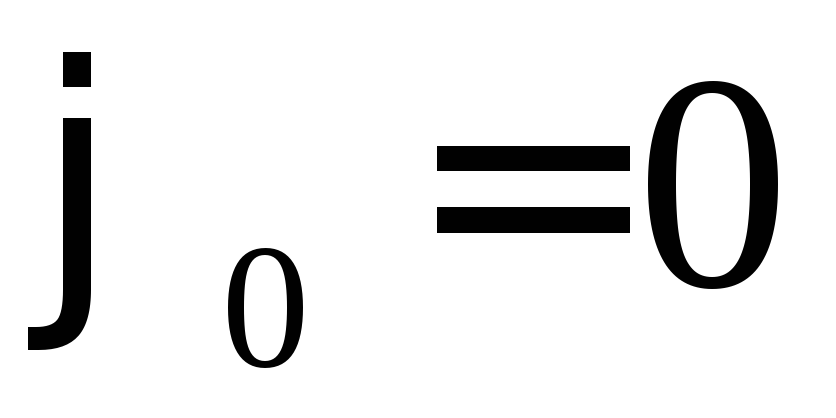, т.е.(рис.17).

Рис.17. Закон сохранения механической энергии

при колебаниях пружинного маятника

При максимальном отклонении груза от положения равновесия полная механическая энергия маятника (энергия деформированной пружины с жесткостью 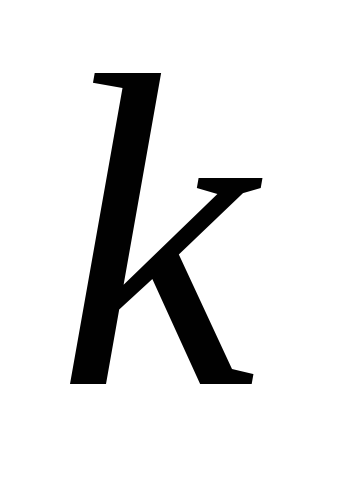) равна 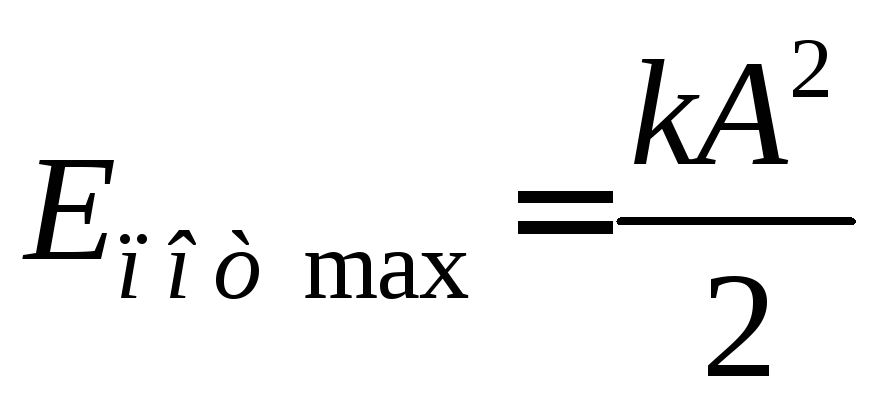. При прохождении положения равновесия (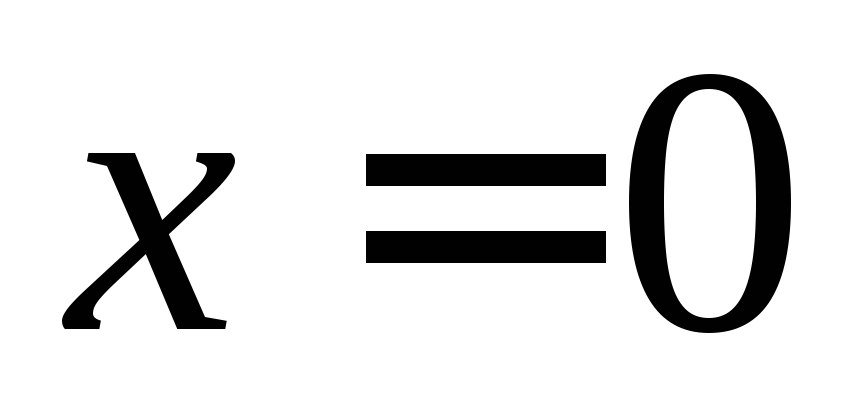) потенциальная энергия пружины станет равной нулю, и полная механическая энергия колебательной системы определится как .

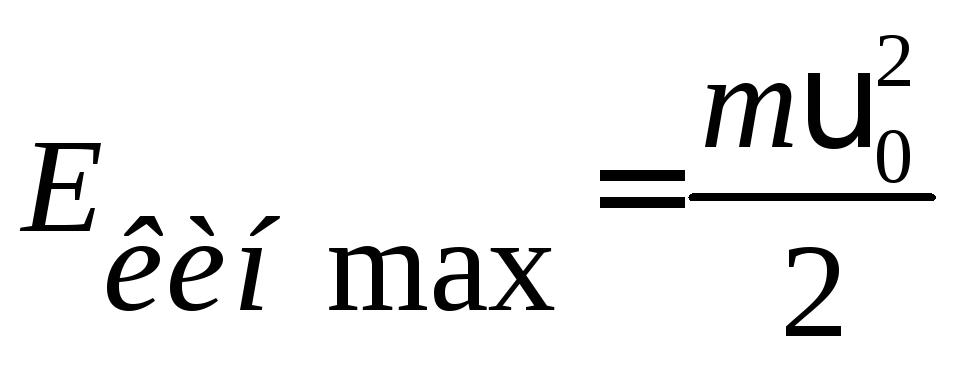На рис.18 представлены графики зависимостей кинетической, потенциальной и полной энергии в случаях, когда гармонические колебания описываются тригонометрическими функциями синуса (пунктирная линия) или косинуса (сплошная линия).

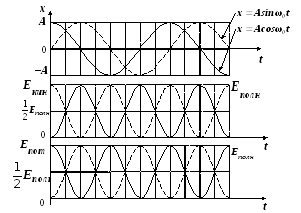
Рис.18. Графики временной зависимости кинетической

и потенциальной энергии при гармонических колебаниях

Из графиков (рис.18) следует, что частота изменения кинетической и потенциальной энергии в два раза выше собственной частоты гармонических колебаний.

Маятник на пружине — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

T = 2 π m k >>> .

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения. Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.

Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

m a = − k x ⟺ x ¨ + k m x = 0 >+ >x=0>

Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:

x ¨ + k m x = f ( x ) >+ >x=f(x)> , где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.

В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:

x ¨ + c m x ˙ + k m x = f ( x ) >+ > >+ >x=f(x)>

Скорость движения маятника формула

Все формулы по физике и математике

Темы по физике

• Механика (56)

• Кинематика (19)
• Динамика и статика (32)
• Гидростатика (5)

• Молекулярная физика (25)
• Уравнение состояния (3)
• Термодинамика (15)
• Броуновское движение (6)
• Прочие формулы по молекулярной физике (1)
• Колебания и волны (22)
• Оптика (9)
• Геометрическая оптика (3)
• Физическая оптика (5)
• Волновая оптика (1)
• Электричество (39)
• Атомная физика (15)
• Ядерная физика (3)
  

  Темы по математике

  • Квадратный корень, рациональные переходы (1)
  • Квадратный трехчлен (1)
  • Координатный метод в стереометрии (1)
  • Логарифмы (1)
  • Логарифмы, рациональные переходы (1)
  • Модуль (1)
  • Модуль, рациональные переходы (1)
  • Планиметрия (1)
  • Прогрессии (1)
  • Производная функции (1)
  • Степени и корни (1)
  • Стереометрия (1)
  • Тригонометрия (1)
  • Формулы сокращенного умножения (1)

  Период математического маятника — период колебания математического маятника зависит от длины нити: с уменьшением длины нити период колебания уменьшается

  

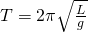
  Для математического маятника выполняются некоторые законы:

  1 закон. Если, сохраняя одну и ту же длину маятника, подвешивать разные грузы (например 5кг и 100 кг), то период колебаний получится один и тот же, хотя массы грузов сильно различаются. Период математического маятника не зависит от массы груза.

  2 закон. Если маятник отклонять на разные, но маленькие углы, то он будет колебаться с одним и тем же периодом, хотя и с разными амплитудами. Пока амплитуда маятника будут малы, колебания и по своей форме будут похожи на гармонические, и тогда период математического маятника не зависит от амплитуды колебаний. Это свойство приняло название изохронизмом..

  

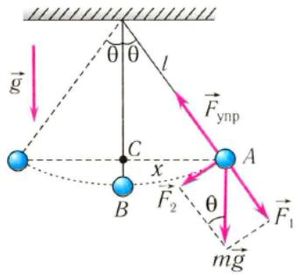
  Давайте выведем формулу периода математического маятника.

  На груз m математического маятника действуют сила тяжести mg и сила упругости нити Fynp. Ось 0Х направим вдоль касательной к траектории движения вверх. Запишем второй закон Ньютона для данного случая:

  

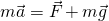
  С проецируем все на ось ОХ:

  

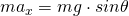
  При малых углах

  

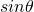
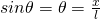
  Сделав замены и маленькие преобразования у нас получается, что уравнение имеет вид:

  

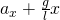
  Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:

  

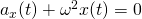
  Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:

  

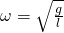
  Тогда период математического маятника будет равен:

  

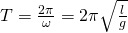
  Период математического маятника зависит только от ускорения свободного падения g и от длины маятника l. Из полученной формулы следует, что период маятника не зависит от его массы и от амплитуды (при условии, что она достаточно мала). Так же мы установили количественную зависимость между периодом маятника, его длиной и ускорением свободного падения. Период математического маятника пропорционален корню квадратному из отношения длины маятника к ускорению свободного падения. Коэффициент пропорциональности равен 2p

  Период пружинного маятника

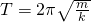
  Период физического маятника

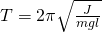
  Период крутильного маятника

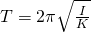
  В Формуле мы использовали :

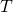  — Период математического маятника

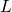  — Длина подвеса

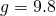  — Ускорение свободного падения

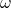  — Циклическая частота пружинного маятника

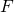  — Сила упругости

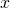  — Длина дуги АВ

  Математическим маятником (осциллятором) называется раскачиваемая механическая система из нерастяжимой нити с пренебрежительно малой массой и подвешенного на ней тела с точечной массой. При описании свойств такого идеального маятника пренебрегают также силами трения и прочими потерями, возникающими при проведении аналогичных опытов в реальных условиях.

  Колебания идеального маятника (зависимость угла отклонения от времени) описываются уравнением:

  $phi(t) = phi_0 cdot cos(omega_0 cdot t + alpha)$,

  • $phi(t)$ – угол отклонения от нижнего положения равновесия в момент $t$,
  • $omega_0$ — циклическая частота,
  • $alpha$ — исходный угол отклонения,
  • $phi_0$ — амплитуда.

  Свойства математического маятника

  Эксперименты, проведенные над маятниками со свойствами, близкими к идеальным, показали их следующие свойства:

  • период колебаний зависит не от массы подвешенного груза, а только от длины нити;
  • при небольших углах отклонения частота колебаний не зависит и от амплитуды (это явление называется изохронизмом).

  Попробуй обратиться за помощью к преподавателям

  Период колебаний идеального маятника можно определить по формуле:

  где $l$ – длина нити математического маятника, $g$ – ускорение свободного падения.

  Применение маятников на практике

  Маятники применяют для создания хронометров. В таких часах период колебаний, отсчитывающих время, регулируют изменением расстояния между точкой крепления подвеса к неподвижной оси и центром тяжести подвешенного груза.

  Колебания маятника математически впервые описал в XVII в. Христиан Гюйгенс, который применил свои теоретические разработки для создания точных механических часов.

  В геодезии зависимость частоты колебаний маятников от изменения силы гравитации используется при определении географической широты.

  Уточнить ускорение свободного падения для данной географической широты, если математический маятник длиной 1 м, совершает колебания с частотой 0,5 Гц (амплитуда колебаний достаточно мала).

  Выразим ускорение из уравнения периода колебаний математического маятника:

  Частота $omega$ — величина обратная периоду колебаний, значит

  Подставив значения, получим

  Ответ: ускорение приблизительно равно $9,8696 м/с^2$

  Задай вопрос специалистам и получи
  ответ уже через 15 минут!

  Определение и формулы математического маятника

  Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.

  Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

  Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

  Читать еще:  Как подключить встраиваемый светильник с подсветкой

  

  Уравнение движения математического маятника

  Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

  где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.

  Решением уравнения (1) является функция $varphi (t):$

  где $alpha $ — начальная фаза колебаний; $ _0$ — амплитуда колебаний; $ _0$ — циклическая частота.

  Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

  Циклическая частота и период колебаний математического маятника

  Циклическая частота математического маятника зависит только от длины его подвеса:

  Период колебаний математического маятника ($T$) в этом случае равен:

  Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

  Уравнение энергии для математического маятника

  При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

  где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:

  Максимальное значение потенциальной энергии математического маятника равно:

  Максимальная величина кинетической энергии:

  где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m= _0x_m$ — максимальная скорость.

  Примеры задач с решением

  Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?

  Решение. Сделаем рисунок.

  

  Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:

  Из уравнения (1.1) найдем искомую высоту:

  Ответ. $h=frac $

  Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми. extit<>

  Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:

  Выразим из нее ускорение:

  Проведем вычисления ускорения силы тяжести:

  Уравнение движения математического маятника

  Математический маятник

  Содержание

  Введение

  Уравнение движения математического маятника

  Период колебаний

  Выводы

  Литература

  Введение

  Сейчас уже невозможно проверить легенду о том, как Галилей, Стоя на молитве в соборе, внимательно наблюдал за качением бронзовых люстр. Наблюдал и определял время, затраченное люстрой на движение туда и обратно. Это время потом назвали периодом колебаний. Часов у Галилея не было, и, чтобы сравнить период колебаний люстр, подвешенных на цепях разной длины, он использовал частоту биения своего пульса.

  Маятники используют для регулировки хода часов, поскольку любой маятник имеет вполне определённый период колебаний. Маятник находит также важное применение в геологической разведке. Известно, что в разных местах земного шара значения g различны. Различны они потому, что Земля — не вполне правильный шар. Кроме того, в тех местах, где залегают плотные породы, например некоторые металлические руды, значение g аномально высоко. Точные измерения g с помощью математического маятника иногда позволяют обнаружить такие месторождения.

  Уравнение движения математического маятника

  Математическим маятником называется тяжёлая материальная точка, которая двигается или по вертикальной окружности (плоский математический маятник), или по сфере (сферический маятник). В первом приближении математическим маятником можно считать груз малых размеров, подвешенный на нерастяжимой гибкой нити.

  Рассмотрим движение плоского математического маятника по окружности радиуса l с центром в точке О (рис. 1). Будем определять положение точки М (маятника) углом отклонения j радиуса ОМ от вертикали. Направляя касательную Mt в сторону положительного отсчёта угла j, составим естественное уравнение движения. Это уравнение образуется из уравнения движения

  mW=F+N, (1)
  где F — действующая на точку активная сила, а N — реакция связи.

  

  Рисунок 1

  Уравнение (1) мы получили по второму закону Ньютона, который является основным законом динамики и гласит, что производная по времени от количества движения материальной точки равна действующей на неё силе, т. е.

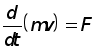  . (2)

  Считая массу постоянной, можно представить предыдущее уравнение в виде

  или ,

  где W есть ускорение точки.

  Итак уравнение (1) в проекции на ось t даст нам одно из естественных уравнений движения точки по заданной неподвижной гладкой кривой:

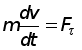  или .

  В нашем случае получим в проекции на ось t

  ,
  где m есть масса маятника.

  Так как или , отсюда находим

  .
  Сокращая на m и полагая

  , (3)
  будем окончательно иметь:

  ,

  ,

  ,

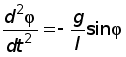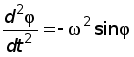  . (4)
  Рассмотрим сначала случай малых колебаний. Пусть в начальный момент маятник отклонён от вертикали на угол j и опущен без начальной скорости. Тогда начальные условия будут:

  при t = 0, 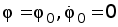. (5)
  Из интеграла энергии:

  , (6)
  где V — потенциальная энергия, а h — постоянная интегрирования, следует, что при этих условиях в любой момент времени угол jЈj₀. Значение постоянной h определяется по начальным данным. Допустим, что угол j₀ мал (j₀Ј1); тогда угол j будет также мал и можно приближённо положить sinj»j. При этом уравнение (4) примет вид

  . (7)
  Уравнение (7) есть дифференциальное уравнение простого гармонического колебания. Общее решение этого уравнения имеет вид

  , (8)
  где A и B или a и e суть постоянные интегрирования.

  Отсюда сразу находим период (T) малых колебаний математического маятника (период — промежуток времени, в течении которого точка возвращается в прежнее положение с той же скоростью)

  и

  ,
  т.к. sin имеет период равный 2p, то wT=2p Ю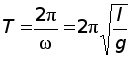

  (9)

  Для нахождения закона движения при начальных условиях (5) вычисляем:

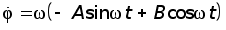  . (10)
  Подставляя значения (5) в уравнения (8) и (10), получим:

  т.е. B=0. Следовательно, закон движения для малых колебаний при условиях (5) будет:

  Найдём теперь точное решение задачи о плоском математическом маятнике. Определим сначала первый интеграл уравнения движения (4). Так как

  ,
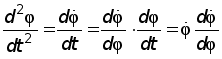  то (4) можно представить в виде

  .
  Отсюда, умножая обе части уравнение на dj и интегрируя, получим:

  . (12)
  Обозначим здесь через j₀ угол максимального отклонения маятника; тогда при j = j₀ будем иметь , откуда C = w 2 cosj₀. В результате интеграл (12) даёт:

  , (13)
  где w определяется равенством (3).

  Этот интеграл представляет собой интеграл энергии и может быть непосредственно получен из уравнения

  , (14)
  где — работа на перемещении M₀M активной силы F, если учесть, что в нашем случае v₀=0, 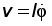и (см. рис.).

  Из уравнения (13) видно, что при движении маятника угол j будет изменяться между значениями +j₀ и -j₀ (|j|Јj₀, так как ), т.е. маятник будет совершать колебательное движение. Условимся отсчитывать время t от момента прохождения маятника через вертикаль OA при его движении право (см. рис.). Тогда будем иметь начальное условие:

  Кроме того, при движении из точки A будет 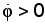; извлекая из обеих частей равенства (13) квадратный корень, получим:

  .
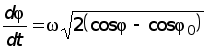  Разделяя здесь переменные, будем иметь: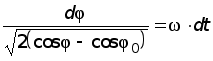

  . (16)

  , ,
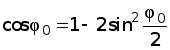  то

  .
  Подставляя этот результат в уравнение (16), получаем:

  . (17)

  Чтобы проинтегрировать уравнение (17), нужно найти квадратуру левой части. Для этого перейдём от j к новым переменному a, полагая:

  , где . (18)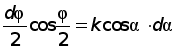

  ,
  откуда

  .
  Кроме того,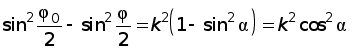

  .
  Подставляя все эти величины в уравнение (17) и заменяя w его значением (3), получим:

  . (19)

  По принятым начальным условиям (15) при t=0 угол j=0, а следовательно, как видно из (18), и a=0. Тогда, беря от обеих частей уравнения (19) определённые интегралы справа от 0 до t, а слева от 0 до a, получим закон движения маятника в виде

  Читать еще:  Как расплавить латунь в домашних условиях видео

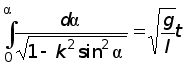  . (20)

  Интеграл, стоящий в левой части равенства (20), представляет собой эллиптический интеграл первого рода. Величина k называется модулем эллиптического интеграла. Этот интеграл есть функция верхнего предела и модуля, т.е.

  . (21)
  Если в равенстве (21) рассматривать верхний предел a как функцию от интеграла u, то такая функция носит название амплитуды u и обозначается так:

  ,
  или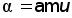

  . (22)

  Беря от обеих частей равенства (22) синус, мы получим:

  . (23)

  Функция snu (синус-амплитуда u) представляет собой так называемую эллиптическую функцию Якоби. Поскольку, согласно уравнению (20), , то, переходя в равенстве (23) от a к j с помощью формулы (18), найдём закон движения маятника, выраженный эллиптическую функцию sn, в виде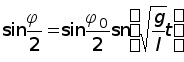

  . (24)

  188.64.169.166 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

  Отключите adBlock!
  и обновите страницу (F5)
  очень нужно

  Скорость движения маятника формула

  

  

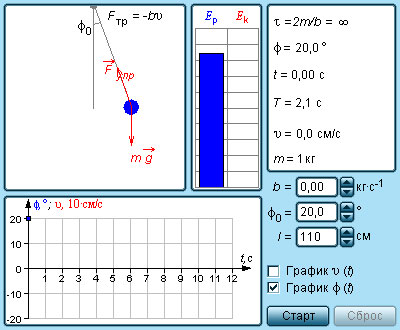
  2.3. Свободные колебания. Математический маятник

  Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести 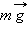уравновешивается силой натяжения нити 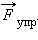При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести F _τ = – mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.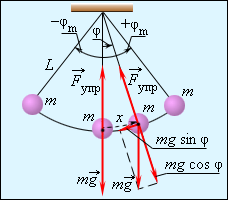

  

  Если обозначить через x линейное смещение маятника от положения равновесия по дуге окружности радиуса l , то его угловое смещение будет равно φ = x / l . Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:

  

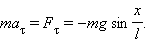
  Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению x , а

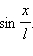
  Только в случае малых колебаний , когда приближенно 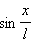можно заменить на 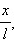математический маятник является гармоническим осциллятором , т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15–20° ; при этом величина 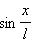отличается от 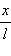не более чем на 2 % . Колебания маятника при больших амплитудах не являются гармоническими.

  Для малых колебаний математического маятника второй закон Ньютона записывается в виде

  

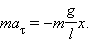
  Таким образом, тангенциальное ускорение a _τ маятника пропорционально его смещению x , взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:

  

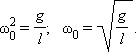
  Эта формула выражает собственную частоту малых колебаний математического маятника .

  

  

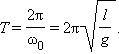
  Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:

  Здесь d – расстояние между осью вращения и центром масс C .

  

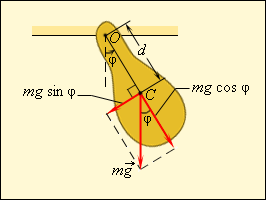
  Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален sin φ . Это означает, что только при малых углах φ , когда sin φ ≈ φ , физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний

  

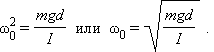
  Здесь ω₀ – собственная частота малых колебаний физического маятника .

  

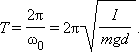
  Более строгий вывод формул для ω₀ и T можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение ε есть вторая производная углового смещения φ по времени:

  

  Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде

  

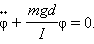
  Это уравнение свободных гармонических колебаний (см. уравнение (*) §2.2). Коэффициент 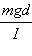в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.

  По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции I можно выразить через момент инерции I _C относительно оси, проходящей через центр масс C маятника и параллельной оси вращения:

  Окончательно для круговой частоты ω₀ свободных колебаний физического маятника получается выражение:

  Подготовка к EГЭ по физике . В1- На установление соответствия (Кодификатор 1.5.1 – 1.5.5). Получение формул периода и максимальной скорости колебаний

  

  Подготовка к EГЭ по физике

  В1- На установление соответствия (Кодификатор 1.5.1 – 1.5.5)

  Получение формул периода и максимальной скорости колебаний

  Что нужно знать (Теория)

  1) Уравнение гармонических колебаний маятника (физического [пружинного] или математического [грузик на нити]

  х – текущая координата (смещение маятника от положения равновесия)

  А – амплитуда колебаний – максимальное смещение от положения равновесия – А=х(max)

  ω0 — собственная циклическая частота колебаний

  (выбор функции cos или sin, а так же сдвиг по фазе, в данных заданиях, думаю, будет не важен)

  

  2) — формула связи циклической частоты и частоты колебаний υ (НЮ)

  3) Используя формулу связи частоты и периода колебаний

  

  4) Формулы периодов маятников от свойств системы

  

  — для математического маятника

  l – длина нити маятника

  g – ускорение свободного падения

  

  — для физического маятника

  m – масса грузика

  k – жёсткость пружины

  5) Скорость – это есть первая производная по перемещению (координате), ускорение – вторая производная по координате:

  

  

  Увы, этот материал в курсе алгебры в 11 классе изучается только в конце года (вот она нестыковка образовательных систем). Поэтому, не вдаваясь в математический аппарат производной от сложной функции, необходимо просто на запоминание выучить ещё две формулы:

  

  

  Чем ещё можно запутать?

  1) Выразить период и частоту колебаний через формулы 7-го класса:

  

  

  t – общее время колебаний маятника

  n – число полных колебаний маятника

  2) Задать исходное уравнение колебаний в непривычном написании. Например

  x = с·sin(b·t + p / 2)

  Здесь самое главное уметь чётко ориентироваться в форме написания формулы

  Пример преобразования формул (математический маятник):

  

  В этих комбинациях, кстати, можно спрятать и период (частоту)

  

  ускорение – вторая производная по координате

  

  Задания для самостоятельного решения

  

  В1-1 . Математический маятник совершает свободные колебания по закону

  За время t он совершает n полных колебаний. Длина нити l. Установите соответствие между физическими величинами, и формулами их описывающими:

  ФИЗИЧЕСКАЯ ВЕЛИЧИНА ФОРМУЛА

  А) Период колебаний маятника 1) 2)

  Б) Максимальная скорость маятника

  

  

  

  В1-2. Математический маятник совершает свободные колебания по закону

  За время t он совершает n полных колебаний. Длина нити l. Установите соответствие между физическими величинами, и формулами их описывающими:

  ФИЗИЧЕСКАЯ ВЕЛИЧИНА ФОРМУЛА

  А) Частота колебаний 1) 2)

  

  

  

  В1-3. Математический маятник совершает свободные колебания по закону

  За время t он совершает n полных колебаний. Длина нити l. Установите соответствие между физическими величинами, и формулами их описывающими:

  ФИЗИЧЕСКАЯ ВЕЛИЧИНА ФОРМУЛА

  А) Максимальная скорость маятника 1) 2)

  Б) Циклическая частота

  

  

  

  В1-4. Математический маятник совершает свободные колебания по закону

  За время t он совершает n полных колебаний. Длина нити l. Установите соответствие между физическими величинами, и формулами их описывающими:

  ФИЗИЧЕСКАЯ ВЕЛИЧИНА ФОРМУЛА

  А) Ускорение 1) 2)

  Б) Период колебаний

  

  3) 4)

  

  В1-5. Физический маятник совершает свободные колебания по закону

  За время t он совершает n полных колебаний. Масса груза – m, жёсткость пружины — k. Установите соответствие между физическими величинами, и формулами их описывающими:

  ФИЗИЧЕСКАЯ ВЕЛИЧИНА ФОРМУЛА

  А) Ускорение 1) 2)

  Б) Циклическая частота

  

  3) 4)

  

  В1-6. Физический маятник совершает свободные колебания по закону

  За время t он совершает n полных колебаний. Масса груза – m, жёсткость пружины — k. Установите соответствие между физическими величинами, и формулами их описывающими:

  ФИЗИЧЕСКАЯ ВЕЛИЧИНА ФОРМУЛА

  А) Период колебаний 1) 2)

  0 0 голоса

  Рейтинг статьи