Расчет зубчатого колеса онлайн

Расчет геометрии зубчатой передачи

Отличительной чертой программы «Расчет геометрии зубчатой цилиндрической эвольвентной передачи», представленной в этой статье, является ее универсальность. С помощью предложенной программы можно выполнить расчет прямозубых и косозубых эвольвентных передач.

. наружного и внутреннего зацепления со смещением исходного контура и без смещения.

В статье «Расчет зубчатой передачи» мной предложена программа «Проектировочный расчет цилиндрической зубчатой передачи», которая на основе заданных силовых и кинематических параметров определяет основные габаритные. Эти величины для сегодняшнего нашего расчета станут исходными данными.

Геометрический расчет зубчатой передачи выполним в программе MS Excel.

Целью данного расчета является нахождение ряда размеров (углов и диаметров), необходимых для окончательного оформления рабочих чертежей колеса и шестерни, а так же для выполнения в дальнейшем проверочных расчетов качества зубчатого зацепления по геометрическим показателям.

Ссылка на файл с программой – в конце статьи.

Схема наиболее распространенного наружного зубчатого зацепления в торцевом сечении показана на рисунке, расположенном ниже этого текста.

Исходные данные записываем в ячейки со светло-бирюзовой заливкой. В ячейки с бледно-голубой заливкой вносим исходные данные, внимательно выполнив требования, помещенные в расположенной над ними строке! Результаты расчетов считываем в ячейках со светло-желтой заливкой. В ячейках со светло-зеленой заливкой, как обычно, помещены мало подверженные изменениям исходные данные.

Открываем таблицу файла Excel и записываем исходные данные:

1. Констатируем в объединенной ячейке D3E3, что параметры нормального исходного контура, участвующие в расчете, взяты по ГОСТ 13755-82. В примечании к объединенной ячейке D3E3 указано: угол исходного профиля a =20 градусов; коэффициент высоты головки зуба ha* =1; коэффициент радиального зазора c* =0,25.

2. Тип зацепления T (смотри примечание: T =1 – наружное; T =-1 – внутреннее зацепление) указываем

в объединенной ячейке D4E4: 1

3. Модуль зацепления m в миллиметрах (в примечании – стандартный ряд модулей) вписываем

в объединенную ячейку D5E5: 1,5

4. Угол наклона зубьев b в градусах (в примечании – рекомендации по назначению) вписываем

в объединенную ячейку D6E6: 13,3222

5. Число зубьев z1 и z2 заносим соответственно

и в ячейку E7: 73

6.1. Далее, если известно из предыдущих расчетов межосевое расстояние aw , то вписываем это значение в миллиметрах

в объединенную ячейку D9E9: _____

Если значение aw не известно, то оставляем ячейку D9E9 пустой! (В примере межосевое расстояние не определено.)

6.2. Если заданы коэффициенты смещения исходного контура x1 и x2 (и соответственно не задано aw !), то вписываем эти значения

в ячейку D10: 0,300

и в ячейку E10: 0,300

Если значения x1 и x2 не заданы, то ничего не записываем в ячейки D10 и E10!

Почему, как и зачем назначать смещение исходного контура, выполняя геометрический расчет зубчатой передачи, мы постараемся обсудить на страницах блога (при наличии интереса аудитории) в статьях, которые будут опубликованы в будущем.

Чтобы не пропустить выход статей, получайте анонсы. Для этого необходимо подписаться в окне, расположенном вверху страницы. Введите адрес своей электронной почты и нажмите на кнопку «Получать анонсы статей», подтвердите подписку в письме, которое тут же придет к вам на указанную почту!

После ввода исходных данных программа расчета геометрии зубчатой передачи представляет первый блок автоматически рассчитанных искомых параметров:

7. Передаточное число u рассчитано

в объединенной ячейке D12E12: =E7/D7 =4,056

u = z2 / z1

8. Делительные диаметры d1 и d2 в миллиметрах вычислены соответственно

в ячейке D13: =D5*D7/COS (D6/180*ПИ()) =27,747

d1 = m * z1 /cos( b )

и в ячейке E13: =D5*E7/COS (D6/180*ПИ()) =112,528

d2 = m * z2 /cos ( b )

9. Делительное межцентровое расстояние A в миллиметрах рассчитано

в объединенной ячейке D14E14: =(E13+D4*D13)/2 =70,137

A =( d2 + T * d1 )/2

10. Угол профиля at в градусах рассчитан

в объединенной ячейке D15E15: =ATAN (TAN (20/180*ПИ())/COS (D6/ 180*ПИ()))/ПИ()*180 =20,5076

at =arctg(tg ( a )/cos ( b ))

11. Диаметры основных окружностей db1 и db2 в миллиметрах вычислены соответственно

в ячейке D16: =D13*COS (D15/180*ПИ()) =25,988

db1 = d1 *cos ( at )

и в ячейке E16: =E13*COS (D15/180*ПИ()) =105,397

db2 = d 2 *cos( at )

12. Угол зацепления atw в градусах рассчитан

в объединенной ячейке D17E17: =ЕСЛИ(D9=0;D50/ПИ()*180;ACOS ( D14*COS (D15/180*ПИ())/D9)/ПИ()*180) =22.2962

Если расстояние между центрами колеса и шестерни не задано, то угол зацепления находится путем решения численным методом трансцендентного уравнения:

tg ( atw ) — atw =2* xs *tg ( a )/( z2 + T * z1 )+ tg ( at ) — at

Подробно о том, как это делается и, что такое трансцендентные уравнения, я постараюсь доступно рассказать в одной из ближайших статей рубрики «Справочник Excel».

Если межосевое расстояние задано, то угол зацепления вычисляется по формуле:

atw =arcos ( A *cos ( at )/ aw )

13. Коэффициент суммы xs (разности — для передач с внутренним зацеплением) смещений вычислен

в объединенной ячейке D18E18: =ЕСЛИ(D9=0;E10+D4*D10;(E7+D4*D7)*((TAN (D17/180*ПИ()) -D17/180*ПИ()) — (TAN (D15/180*ПИ()) -D15/180*ПИ()))/(2*TAN (20/180*ПИ()))) =0,6000

Если межцентровое расстояние не задано, то коэффициент суммы (разности) находится по формуле:

xs = x 2 + T * x1

Если межцентровое расстояние задано, то коэффициент суммы (разности) вычисляется по формуле:

xs =( z2 + T * z1 )*((tg ( atw ) — atw ) — (tg ( at ) — at ))/(2*tg ( a ))

Далее – короткая работа интеллекта инженера, и программа завершает геометрический расчет в Excel зубчатой передачи:

14. Если коэффициенты смещения были заданы, то просто повторно записываем значение x1

в ячейку D20: 0,3000

Если коэффициенты смещения x1 и x2 изначально заданы не были (было задано межосевое расстояние aw ), то на этом этапе необходимо произвести разбивку вычисленного коэффициента суммы (разности) смещений xs и записать в ячейку D20 значение x1 .

Рекомендации по разбивке коэффициента суммы (разности) смещений можно посмотреть в ГОСТ 16532-70 и в соответствующих справочниках (в том числе В.И.Анурьева).

Значение коэффициента смещения x2 вычисляется автоматически

в ячейке E20: =D18-D4*D20 =0,3000

x2 = xs — T * x1

15. Межосевое расстояние передачи aw в миллиметрах, если не задано — вычислено, если задано – автоматически повторено

в объединенной ячейке D21E21: =ЕСЛИ(D9=0;D14*COS (D15/180* ПИ())/COS (D17/180*ПИ());D9) =71,001

aw = A *cos ( at )/cos ( atw )

16. Диаметры начальных окружностей dw1 и dw2 в миллиметрах вычислены соответственно

в ячейке D22: =2*D21/(D12+1)=28.088

dw1 =2* aw /( u +1)

и в ячейке E22: =2*D21*D12/(D12+1) =113.914

dw2 =2* aw * u /( u +1)

17. Коэффициент уравнительного смещения dy рассчитан

в объединенной ячейке D23E23: =D18- (D21-D14)/D5 =0.0243

dy = xs — ( aw — A )/ m

18. Диаметры вершин зубьев шестерни и колеса da1 и da2 в миллиметрах вычислены соответственно

в ячейке D24: =D13+2*D5*(1+D20-D23) =31.574

da1 = d 1 +2* m *(( ha * )+ x 1 — dy )

и в ячейке E24: =E13+2*D5*D4*(1+D4*E20-D23) =116.355

da2 = d2 +2* m * T *(( ha* )+ T * x2 — dy )

В обоснованных случаях значения, полученные расчетом конструктор вправе изменить, обеспечив качественные характеристики зацепления.

19. Диаметры впадин шестерни и колеса df1 и df2 в миллиметрах вычислены соответственно

в ячейке D25: =D24-2*D5*(2*1+0,25-D23) =24.897

df1 = da 1 -2* m *(2*( ha * )+( c * ) — dy )

и в ячейке E25: =E24-2*D5*D4*(2*1+0,25-D23) =109.678

df2 = da2 -2* m * T *(2*( ha* )+( c* ) — dy )

На этом геометрический расчет в Excel цилиндрической зубчатой передачи, целью которого было определение всех основных размеров зацепления завершен. При создании расчетной программы была объединена и переработана информация из ГОСТ 16532-70 и ГОСТ 19274-73.

Следующим этапом проектирования зубчатых передач являются проверочные расчеты качества зацепления по геометрическим показателям.

Еще по теме зубчатых колес на блоге есть ряд статей. Рекомендую ознакомиться, в частности, со статьей «Расчет длины общей нормали зубчатого колеса».

Буду рад увидеть ваши комментарии к посту, уважаемые читатели!

Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.

Ссылка на скачивание файла: geometriya-zubchatoy-peredachi (xls 42,5KB).

Модуль зубьев зубчатого колеса

Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

Скачать ГОСТ 9563-60

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

где h — высота зубца.

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Расчет параметров колеса и шестерни косозубой передачи

Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Расчет реечной передачи онлайн

Цилиндрические шестерни → Реечная передача

Для преобразования вращательного движения в поступательное и наоборот применяют реечную передачу, которая является частным случаем цилиндрической зубчатой передачи. Рейку рассматривают как зубчатое колесо, диаметр которого увеличен до бесконечности.

ЗАО «НПО «Механик» изготавливает цилиндрические реечные передачи со следующими характеристиками:

— Класс точности — до 6 включительно;

— Модуль — до 30 включительно;

— Длина рейки — до 3 500 мм включительно.

Изготавливаем цилиндрические реечные передачи в штучном и серийном производстве. Возможно изготовление по образцам и эскизам заказчика. Индивидуальный подход.

Реечная передача отличается простотой конструкции, благодаря чему она надежна в эксплуатации. Кроме этого у реечной передачи достаточно высокий КПД (0,94 — 0,98). Составляющие реечной передачи изготавливаются из относительно недорогих углеродистых конструкционных или легированных сталей. К недостаткам реечной передачи можно отнести то, что ее передаточное число равно 1 и поэтому выигрыш в силе отсутствует.

Основной размерный параметр зубчато-реечной передачи — шаг между зубьями рейки. Шаг рейки может рассчитываться по метрической или по модульной системе. В модульной системе расстояние между зубьями рейки рассчитывается по формуле:

m = D/z,

где m — модуль пары рейка-шестерня;
z — количество зубьев шестерни;
D — делительный диаметр шестерни (диаметр окружности, проходящей через полувысоту зуба шестерни; для некорригированных зацеплений начальные и делительные окружности совпадают).

Поскольку значение модуля дробное и представляет собой бесконечную десятичную дробь, для расчетов применяют его округленное значение. В передачах рейка-шестерня используют общепринятые значения модуля в пределах от 0,5 до 25 мм.

В метрической системе расстояние между зубьями рейки измеряется в миллиметрах. Метрическая система применяется в случаях, когда по технологии производства передачи зубчатое колесо подбирается под рейку, а модульная — наоборот, когда зубчатая рейка подбирается под шестерню. Модульная система, соответственно, используется преимущественно в производстве комплектных приводов (серийный мотор-редуктор, шестерня, рейка), а метрическая — для решений в области модернизации или построения нестандартных машин и механизмов.

При вращении зубчатого колеса вокруг неподвижной оси зубчатая рейка перемещается прямолинейно-поступательно при каждом обороте колеса на величину S, равную длине начальной окружности зубчатого колеса (в мм), т. е.:

S = π·d = π·m·z,

где d — диаметр начальной окружности зубчатого колеса, мм;
m — модуль зубчатой рейки, мм;
z — число зубьев колеса.

Вместо зубчатой рейки можно заставить перемещаться зубчатое колесо, в этом случае путь пройдет не зубчатая рейка, а ось реечного зубчатого колеса при перекатывании по неподвижной зубчатой рейке.

Зная число оборотов зубчатого колеса в минуту реечной передачи, скорость, с которой перемещается зубчатая рейка, рассчитывают по формуле:

v =π·D·n/1000 = π·m·z·n/1000

где v — скорость перемещения зубчатой рейки, м/мин;

n — число оборотов в минуту зубчатого колеса.

Зубчато-реечные передачи выполняются с прямыми зубьями для работ на малых и средних скоростях, с косыми зубьями для использования на средних и высоких скоростях или когда требуется повышенная точность перемещения.

Базовыми поверхностями рейки называют поверхности, относительно которых задается положение делительной прямой и направление зуба рейки.

По вопросам изготовления реечных передач с прямым и косым зубом обращайтесь в отдел продаж по телефону:

Расчет зубчатого колеса

1. Число зубьев шестерни z=20
2. Модуль m=1,5 мм.
3.Угол профиля α=20°
4. Делительный диаметр d1=z*m=20*1.5=30 мм.
5. Межосевое расстояние между рейкой и колесом а=d1/2=30/2= 15мм.
6. Диаметр вершины зуба da1=d1+2m=30+2*1,5=33 мм.
7. Диаметр впадины зуба df1=d1-2(c+m)=30-2*(0,375+1,5)=26.25 мм.
8. Постоянная хорда ss=1,387*m=2,08 мм.
9. Высота до постоянной хорды hc=0,748*m=1,12 мм.

Расчет рейки

1. Угол профиля зуба рейки α=20°
2. Угол наклона рекомендуется применять не более 20° 3. Модуль нормальный mn=1,5 мм.
4. Модуль основной(торцевой) mt=mn/cоsβ=1,5/cоs20°=1,6 мм.
5.Шаг нормальный pn=π*mn=4,71 мм.
6. Шаг торцевой pt=(π*mn)/cоsβ=5 мм.
7. Высота головки зуба ha=mn=1,5 мм.
8. высота зуба h=2,25*mn=3,375 мм.
9. Ширина рейки b=(2÷10)*mn=12 мм.
10. Рабочая длина нарезаемой части L=25 мм.

(Статья полностью обновлена 19.03.2017.)

Небольшой расчет, представленный далее, предназначен для ориентировочного быстрого определения габаритов зубчатой реечной передачи и её основных силовых и кинематических параметров.

Предложенный ниже алгоритм основан на расчете поверхностной прочности зубьев по контактным напряжениям.

Реечная передача может служить для преобразования вращательного движения шестерни в поступательное движение рейки или вала самой шестерни, а может быть использована для преобразования поступательного движения рейки во вращательное движение зубчатого колеса. Расчет реечной передачи, по сути, аналогичен расчету зубчатой цилиндрической передачи. С математической точки зрения рейка – это зубчатое колесо с радиусом равным бесконечности.

Проектировочный расчет в Excel реечной зубчатой передачи.

Для выполнения расчетов будем использовать программу MS Excel или Calc из бесплатных офисных пакетов Apache OpenOffice или LibreOffice.

Заполняя исходные данные для расчета, пользователь может изменять характеристики используемого для передачи материала, относительную ширину и угол наклона зубьев, нагрузку и скорость.

Схема реечной передачи представлена на рисунке чуть ниже.

Уважающих труд автора прошу скачивать файл с расчетной таблицей после подписки на анонсы статей (подписные формы — в конце статьи и наверху страницы).

Ссылка на скачивание файла с программой: reyechnaya-peredacha (xls 59KB).

Исходные данные:

1. Значение модуля упругости материала передачи E в МПа записываем

в ячейку D3: 215000

Для стали E =215000 МПа.

2. Коэффициент Пуассона материала μ вписываем

в D4: 0,3

3. Твердость поверхности зубьев по шкале C Роквелла HRC вводим

в D5: 27

Для различных режимов термообработки стали HRC ≈17…65.

К примеру, круг из Стали 45 в состоянии поставки имеет твердость около HRC 22.

4. Величину безразмерного коэффициента ширины зубчатого венца шестерни ψ _bd заносим

в D6: 0,6

ψ_bd = b₂ / d =0,6…0,4.

5. Угол наклона зубьев β вводим в градусах

в D7: 15,0000

Если проектируемая реечная передача прямозубая, то β =0°.

Если передача косозубая, то β ≈8°…22°.

6. Вращательный момент на валу шестерни T вписываем в Н*м

в D8: 500

Этот момент определяет нагрузочную способность реечной передачи и задается в техническом задании.

7. Скорость центра вала шестерни относительно рейки v в м/с заносим

в D9: 0,050

Скорость определяется из назначения механизма и является одним из пунктов технического задания на проектирование.

Результаты расчетов:

8. Допускаемое контактное напряжение [σ_H] в МПа вычисляем

в ячейке D11: =ЕСЛИ(D5 =600,0

При HRC [σ_H] =2*127,57*e (0,0266* HRC ) +70

При 38≤ HRC ≤56 [σ_H] =18* HRC +150

При HRC ≥56 [σ_H] =23* HRC

9. Расчетный делительный диаметр d _p в мм вычисляем

в D12: =(2*2*D8*1000*D3/(ПИ()*(1-D4^2)*D11^2*D6*SIN (2*20/180* ПИ())))^(1/3) =102,7

d_p ≥(4000* T * E /(π*(1- μ 2 )* [σ_H] 2 * ψ_bd *sin(2* α ) (1/3)

10. Расчетный модуль зацепления m _p в мм определяем

в D13: =D12/(17*COS (D7/180*ПИ())^3) =6,70

m_p = d_p /(17*(cos ( β )) 3 )

11. Выбираем ближайшую к расчетному значению величину модуля m из стандартного ряда, представленного в примечании к ячейке D14, и вписываем

в D14: 6,00

12. Минимальное расчетное число зубьев шестерни z ₁ рассчитываем

в D15: =17*COS (D7/180*ПИ())^3 =15,3

z₁ =17*(cos ( β )) 3

Число зубьев шестерни определяется из условия отсутствия подрезки ножек зубьев.

13. Назначаем число зубьев шестерни z₁ и записываем его

в D16: 17

Рекомендуется назначить число зубьев таким, чтобы делительный диаметр шестерни был не меньше расчетного делительного диаметра.

14. Делительный диаметр шестерни d в мм вычисляем

в D17: =D14*D16/COS (D7/180*ПИ()) =105,598

d = m * z₁ /cos ( β )

Если полученное значение делительного диаметра окажется меньше расчетного значения, поле ячейки D15 «подсветится» красным цветом, что заставит пользователя обратить внимание на ошибку и увеличить число зубьев, модуль или угол наклона зубьев.

15. Диаметр вершин зубьев шестерни d _a в мм находим

в D18: =D17+2*D14 =117,598

d_a = d +2* m

16. Диаметр впадин зубьев шестерни d_f в мм рассчитываем

в D19: =D17-2,5*D14 =90,598

d_f = d -2,5* m

17. Ширину зубчатого венца шестерни b₁ в мм считаем

в D20: =ОКРУГЛ(D21+0,6*D21^0,5;0) =68

b₁ ≈ b₂ +0,6* b₂ (½)

18. Ширину зубьев рейки b ₂ в мм находим

в D21: =ОКРУГЛ(D17*D6;0) =63

b₂ ≈ d * ψ_bd

19. Окружную силу на шестерне F_t в Н рассчитываем

в D22: =2*D8/(D17/1000) =9470

F_t =2* T / d

20. Мощность на валу шестерни P в Вт вычисляем

в D23: =D22*D9 =473

P = F_t * v

21. Частоту вращения вала шестерни n в об/мин определяем

в ячейке D24: =60*D9/ПИ()/(D17/1000) =9,043

n =60* v /(π* d )

Расчет в Excel завершен.

Заключение.

Мы рассмотрели пример, в котором была рассчитана зубчатая реечная передача по упрощенной схеме.

Детальный и полный расчет передачи, учитывающий десяток дополнительных факторов, может позволить на 5%. 10% уменьшить габаритные размеры передачи! Это следует понимать и помнить.

Если требуется уменьшить число зубьев шестерни менее 14-и, необходимо спроектировать и изготовить её возможно не только с наклоном зубьев, но и/или с положительным смещением исходного контура. При этом нужно следить за отсутствием заострения вершин зубьев, производя соответствующую проверку.

Важными параметрами, обеспечивающими плавность работы реечной передачи, являются коэффициенты осевого и торцевого перекрытия. Их значения всегда следует контролировать.

О проверке качества зубчатого зацепления по геометрическим показателям читайте в следующих новых статьях на блоге.

Подписаться на анонсы статей можно через специальные окна, расположенные в конце любой статьи или наверху любой страницы сайта.

Можете оставлять ваши комментарии, уважаемые читатели, ниже этого текста в блоке «Отзывы».

Шестерёнка — методика построения для любой CAD системы

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых постах.

Отписаться от уведомлений вы всегда сможете в профиле автора.

Про моделирование и печать шестеренок здесь написано достаточно. Однако, большинство статей предполагают использование спец. программ. Но, у каждого пользователя есть своя «любимая» программа для моделирования. Кроме того, не все хотят устанавливать и изучать дополнительный софт. Как же моделировать профиль зуба шестерни в программе, где не предусмотрено вычерчивание эвольвентного профиля? Очень просто! Но муторно… 🙂

Нам понадобится любая программа, которая может работать с 2D графикой. Например, ваша любимая программа! Она работает с 3D? Значит и с 2D сможет! 😉 Строим профиль эвольвентного зуба без коррекции. Если кому-то захочется построить корригированный зуб, он может с этим разобраться самостоятельно. Информации полно — и в интернете, и в литературе. Если в вашей шестеренке зубьев больше 17-ти, то вам коррекция не понадобится. Если же зубьев 17 или меньше, то без коррекции возникает «утоньшение» ножки зуба, а при чрезмерной коррекции возникает заострение вершины зуба. Что выбрать? Решать вам.

Определяем делительную окружность шестерни. Зачем это нужно? Чтобы определить межосевое расстояние. Т.е. где у вас будет располагаться одна шестерня, а где другая. Сложив диаметры делительных окружностей шестеренок и разделив сумму пополам, вы определите межосевое расстояние.

Чтобы определить диаметр делительной окружности нужно знать два параметра: модуль зуба и количество зубьев. Ну, с количеством зубьев – тут всем все понятно. Количеством зубьев на одной и другой шестерне определяется нужное нам передаточное отношение. Что такое модуль? Чтобы не связываться с числом «пи», инженеры придумали модуль. 🙂 Как вы знаете из курса школьной математики: D= 2 «Пи» R. Так вот, что касается шестеренок, там D = m* z, где D – это диаметр делительной окружности, m – модуль, z – количество зубьев. Модуль – величина, характеризующая размер зуба. Высота зуба равна 2,25 m. Модуль принято выбирать из стандартного ряда величин: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32 (ГОСТ-9563). Можно ли придумать «свой» модуль? Конечно! Но ваша шестеренка будет нестандартная! 😉

Чертим делительную окружность. У кого нет подходящей «проги», чертит на бумаге, фанере или металле! 🙂 От делительной окружности «откладываем» наружу на величину модуля (m) окружность вершин зубьев. Внутрь откладываем модуль и еще четверть модуля (1,25 m) — получаем окружность впадин зубьев. Четверть модуля дается на зазор между зубом другой шестерни и впадиной этой шестерни.

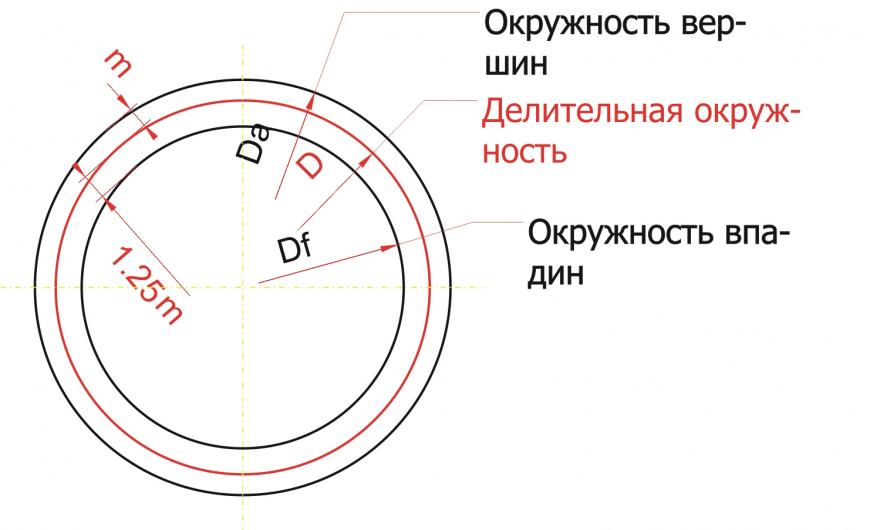
Строим основную окружность. Основная окружность – это окружность, по которой «перекатывается» прямая линия, своим концом вычерчивая эвольвенту. Формула для расчета диаметра основной окружности очень простая: Db = D * cos a, где а – угол рейки 20 градусов. Эта формула нам не нужна! Все гораздо проще. Строим прямую линию через любую точку делительной окружности. Удобнее взять самую высокую точку, на «12 часов». Тогда линия будет горизонтальная. Повернем эту линию на угол в 20 градусов против часовой стрелки. Можно ли повернуть на другой угол? Думаю, можно, но не нужно. 🙂 Кому интересно, ищем в литературе или интернете ответ на вопрос.

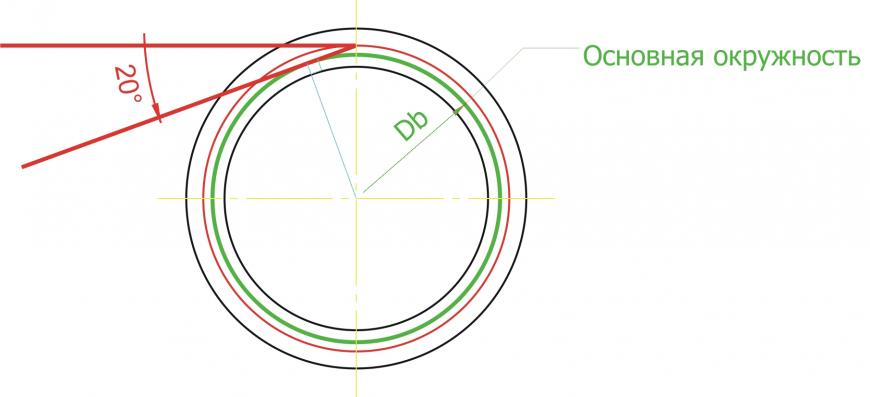
Прямую линию, которую мы получили, будем поворачивать вокруг центра шестерни маленькими угловыми шагами. Но, самое главное, при каждом повороте против часовой стрелки будем удлинять нашу линию на длину той дуги основной окружности, которую она прошла. А при повороте по часовой стрелки наша линия будет укорачиваться на ту же величину. Длину дуги или мерим в программе, или считаем по формуле: Длина дуги = (Пи * Db * угол поворота (в градусах)) / 360

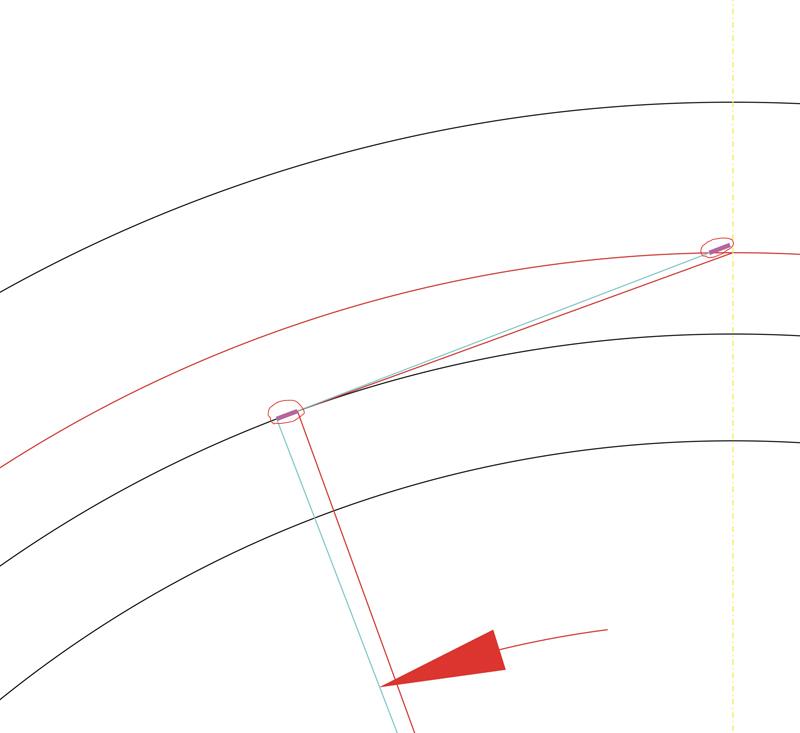
«Прокатываем» прямую линию по основной окружности с нужным угловым шагом. Получаем точки эвольвентного профиля. Чем точнее хотим строить эвольвенту, тем меньший угловой шаг выбираем.

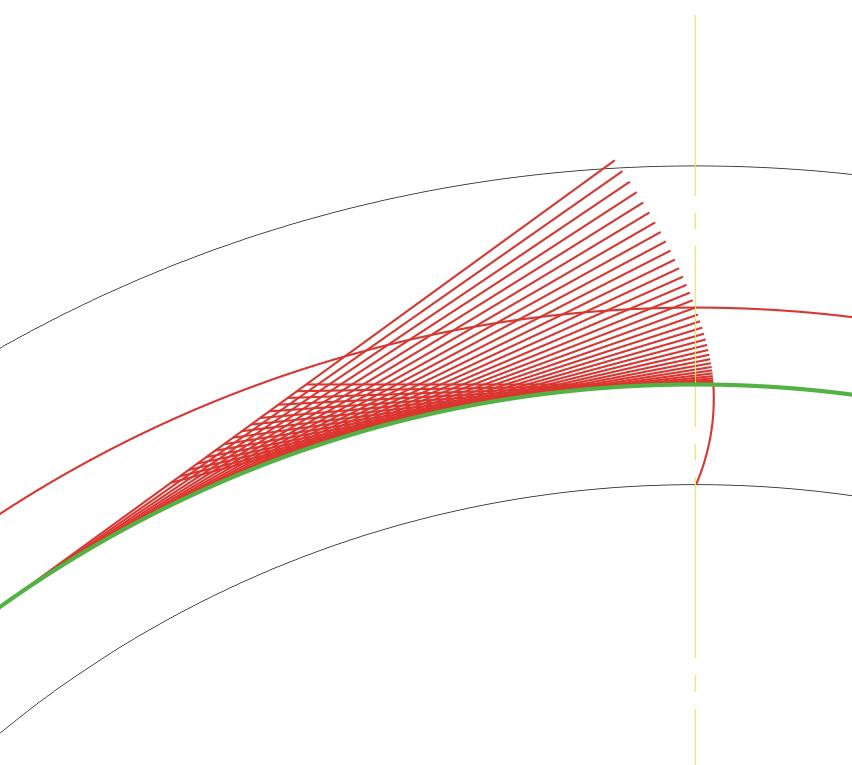
К сожалению, в большинстве программ автоматического проектирования (CAD) не предусмотрено построение эвольвенты. Поэтому эвольвенту строим по точкам либо прямыми, либо дугами, либо сплайнами. При построении эвольвента заканчивается на основной окружности. Оставшуюся часть зуба до впадины можно построить дугой того же радиуса, который получается на трех последних точках. Для 3D печати я рисовал эвольвенту сплайнами. Для лазерной резки металла мне пришлось рисовать эвольвенту дугами. Для лазера нужно создать файл в формате dwg или dxf (для некоторых, почему-то, только dxf). «Понимает» лазер только прямые, дуги и окружности, сплайны не понимает. На лазере можно сделать только прямозубые шестерни.

Делим окружность на такое количество частей, которое в 4 раза больше количества зубьев шестерни. Эвольвенту отзеркаливаем относительно оси зуба и копируем с поворотом нужное количество раз.

Чтобы получить шестерню в объеме, то задаем толщину и получаем прямозубую цилиндрическую шестерню:

Если нужна косозубая шестерня, то вводим наклон зубьев и получаем:

Для получения шевронной шестерни, нужно отзеркалить косозубую шестерню относительно нужной торцевой поверхности:

Как смоделировать коническую шестерню, придумайте сами. 🙂

К вопросу о точности шестеренок. Те шестеренки, которые я распечатал на 3D принтере, сначала вращались, издавая легкое поскрипывание. Прошло некоторое время, и звук прекратился. Шестеренки «притерлись». 🙂

После модернизации принтера, шестеренки не печатал. Возможно, сейчас они напечатаются более точно, и не будут скрипеть.

Для вакуумной машины смоделировал пару – «шестерня-рейка». Их вырезали на лазере:

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых постах.

Отписаться от уведомлений вы всегда сможете в профиле автора.

Подбор сменных зубчатых колес. Программа для подбора

Программа для подбора сменных зубчатых колес

ПОРЯДОК ПОЛЬЗОВАНИЯ ТАБЛИЦАМИ / ПРОГРАММОЙ

Для подбора сменных колес искомое передаточное отношение выражается в виде десятичной дроби с числом знаков соответственно требуемой точности. В «Основных таблицах» для подбора зубчатых колес (стр. 16—400) находим колонку с заголовком, содержащим первые три цифры передаточного отношения; по остальным цифрам находим строку, на которой указаны числа зубьев ведущих и ведомых колес.

Требуется подобрать сменные колеса гитары для передаточного отношения 0,2475586. Сначала находим колонку с заголовком 0,247—0000, а под ним ближайшее значение к последующим десятичным знакам искомого передаточного отношения (5586). В таблице находим число 5595, соответствующее набору сменных колес (23*43) : (47*85). Окончательно получаем:

i = (23*43)/(47*85) = 0,2475595. (1)

Относительная погрешность сравнительно с заданным передаточным отношением :

δ = (0,2475595 — 0,2475586) : 0,247 = 0,0000037.

Строго подчеркиваем: во избежание влияния возможной опечатки нужно обязательно проверить полученное соотношение (1) на калькуляторе. В тех случаях, когда передаточное отношение больше единицы, необходимо выразить его обратную величину в виде десятичной дроби, по найденному значению в таблицах отыскать числа зубьев ведущих и ведомых сменных колес и поменять ведущие и ведомые колеса местами.

Требуется подобрать сменные колеса гитары для передаточного отношения i = 1,602225. Находим обратную величину 1:i = 0,6241327. В таблицах для ближайшего значения 0,6241218 находим набор сменных колес: (41*65) : (61*70). Учитывая, что решение найдено для обратной величины передаточного отношения, меняем местами ведущие и ведомые колеса:

i = (61*70)/(41*65) = 1,602251

Относительная погрешность подбора

δ = (1,602251 — 1,602225) : 1,602 = 0,000016.

Обычно требуется подбирать колеса для передаточных отношений, выраженных с точностью до шестого, пятого, а в отдельных случаях и до четвертого десятичного знака. Тогда семизначные числа, приведенные в таблицах, можно округлять с точностью до соответствующего десятичного знака. Если имеющийся комплект колес отличается от нормального (см. стр. 15), то, например, при настройке цепей дифференциала или обкатки можно выбрать подходящую комбинацию из ряда соседних значений с погрешностью, удовлетворяющей условиям, изложенным на стр. 7—9. При этом некоторые числа зубьев можно заменять. Так, если число зубьев комплекта не свыше 80, то

(58*65)/(59*95) = (58*13)/(59*19) = (58*52)/(59*76)

«пятковую» комбинацию предварительно преобразуют так:

а затем, по полученным множителям подбирают числа зубьев.

ОПРЕДЕЛЕНИЕ ДОПУСТИМОЙ ПОГРЕШНОСТИ НАСТРОЙКИ

Очень важно различать абсолютную и относительную погрешности настройки. Абсолютной погрешностью называют разность между полученным и требуемым передаточными отношениями. Например, требуется иметь передаточное число i = 0,62546, а получено i = 0,62542; абсолютная погрешность будет 0,00004. Относительной погрешностью называют отношение абсолютной погрешности к требуемому передаточному числу. В нашем случае относительная погрешность

δ = 0.00004/0,62546 = 0,000065

Следует подчеркнуть необходимость суждения о точности настройки по относительной погрешности.

Общее правило.

Если какая-либо величина А, получаемая настройкой через данную кинематическую цепь, пропорциональна передаточному отношению i, то при относительной погрешности настройки δ абсолютная погрешность будет Аδ.

Например, если относительная погрешность передаточного отношения δ =0,0001, то при нарезании винта с шагом t отклонение в шаге, зависящее от настройки, будет 0,0001 * t. Та же относительная погрешность при настройке дифференциала зубофрезерного станка даст дополнительное вращение заготовки не на требуемую дугу L, а на дугу с отклонением 0,0001 * L.

Если указан допуск на изделие, то абсолютное отклонение размера вследствие неточности настройки должно составлять только некоторую долю этого допуска. В случае более сложной зависимости какой-либо величины от передаточного отношения полезно прибегать к замене фактических отклонений их дифференциалами.

Настройка цепи дифференциала при обработке винтовых изделий.

Типичной является следующая формула:

где с — постоянная цепи;

β — угол наклона винтовой линии;

n — число заходов фрезы.

Продифференцировав обе части равенства, получим абсолютную погрешность di передаточного отношения

тогда допустимая относительная погрешность настройки

Если допустимое отклонение угла винтовой линии dβ выразить не в радианах, а в минутах, то получим

Например, если угол наклона винтовой линии изделия β = 18°, а допустимое отклонение в направлении зуба dβ = 4″ = 0′,067, то допустимая относительная погрешность настройки

δ = 0,067/3440*tg18 = 0,00006

Наоборот, зная относительную погрешность взятого передаточного отношения, можно по формуле (3) определить допущенную погрешность в угле винтовой линии в минутах. При установлении допустимой относительной погрешности можно в подобных случаях пользоваться тригонометрическими таблицами. Так, в формуле (2) передаточное отношение пропорционально sin β. По тригонометрическим таблицам для взятого числового примера видно, что sin 18° = 0,30902, а разность синусов на 1′ составляет 0,00028. Следовательно, относительная погрешность на 1′ составляет 0,00028 : 0,30902 = 0,0009. Допустимое отклонение винтовой линии — 0,067, поэтому допустимая погрешность передаточного отношения 0,0009*0,067 = 0,00006, такая же, как и при расчете по формуле (3). Когда оба сопряженных колеса нарезаются на одном станке и по одной настройке цепи дифференциала, то погрешности в направлении линий зубьев допускаются значительно большие, так как у обоих колес отклонения одинаковы и незначительно влияют только на боковой зазор при зацеплении сопряженных колес.

Настройка цепи обкатки при обработке конических колес.

В этом случае формулы настройки выглядят так:

i = p*sinφ/z*cosу или i = z/p*sinφ

где z — число зубьев заготовки;

р — постоянная цепи обкатки;

φ — угол начального конуса;

у — угол ножки зуба.

Пропорциональным передаточному отношению оказывается радиус основной окружности. Исходя из этого, можно установить допустимую относительную погрешность настройки

где α — угол зацепления;

Δα — допустимое отклонение угла зацепления в минутах.

Настройка при обработке винтовых изделий.

δ = Δt/t или δ = ΔL/1000

где Δt — отклонение в шаге винта за счет настройки;

ΔL — накопленная погрешность в мм на 1000 мм длины резьбы.

Величина Δt дает абсолютную ошибку шага, а величина ΔL характеризует по существу относительную погрешность.

Настройка с учетом деформации винтов после обработки.

При нарезании метчиков с учетом усадки стали после последующей термической обработки или с учетом деформации винта вследствие нагревания при механической обработке, процент усадки или расширения непосредственно указывает на необходимое относительное отклонение в передаточном отношении сравнительно с тем, какое получилось бы без учета этих факторов. В этом случае относительное отклонение передаточного отношения в плюс или минус является уже не ошибкой, а преднамеренным отклонением.

Настройка делительных цепей. Типичная формула настройки

где р — постоянная;

z — число зубьев или других делений на один оборот заготовки.

Нормальный комплект из 35 колес обеспечивает абсолютно точную настройку до 100 делений, так как в числах зубьев колес содержатся все простые множители до 100. В такой настройке погрешность вообще недопустима, так как она равна:

где Δl — отклонение линии зуба на ширине заготовки В в мм;

пD — длина начальной окружности или соответствующей другой окружности изделия в мм;

s — подача вдоль оси заготовки на один ее оборот в мм.

Только в грубых случаях эта погрешность может не играть роли.

Настройка зубофрезерных станков при отсутствии требуемых множителей в числах зубьев сменных колес.

В таких случаях (например, при z = 127) можно настроить гитару деления приближенно на дробное число зубьев, а необходимую поправку произвести, используя дифференциал [5]. Обычно формулы настройки гитар деления, подач и дифференциала выглядят так:

x = pa/z ; y = ks ; φ = c*sinβ/ma

Здесь р, k, с — соответственно постоянные коэффициенты этих цепей; а — число заходов фрезы (обычно а = 1).

Настраиваем указанные гитары согласно формулам

x = paA/Az+-1 ; y = ks ; φ’ = пc/asA

где z — число зубьев обрабатываемого колеса;

А — произвольное целое число, выбираемое так, чтобы числитель и знаменатель передаточного отношения разлагались на множители, подходящие для подбора сменных колес.

Знак (+) или (—) также выбирается произвольно, что облегчает разложение на множители. При работе правой фрезой, если выбран знак (+), промежуточные колеса на гитарах ставятся так, как это делают согласно руководству по работе на данном станке для правовинтовой заготовки; если выбран знак (—), промежуточные колеса ставят, как для левовинтовой заготовки; при работе левой фрезой — наоборот.

Желательно выбирать А в пределах

(1/2)*(пc/as) b+(20. 25); b + d > с+(20. 25) (11)

Эти условия ставятся для предотвращения упора сменных колес в соответствующие валы или детали крепления; числовое слагаемое зависит от конструкции данной гитары. Однако вторая из комбинаций (10) может быть принята только в том случае, когда колесо Z2 устанавливается на первом ведущем валу и если передача z2/z3 замедляющая или не содержит большого ускорения. Желательно, чтобы z2/z3 1) желательно так разбивать i = i1i2 чтобы сомножители были возможно более близкими один к другому и равномернее распределялось повышение скорости. При этом лучше, если i1 > i2

МИНИМАЛЬНЫЕ КОМПЛЕКТЫ СМЕННЫХ КОЛЕС

Состав комплектов сменных колес в зависимости от области применения приведен в табл. 2. В случае особо точных настроек — см. стр. 403.

Числа зубьев минимальных комплектов сменных колес для различных случаев настроек

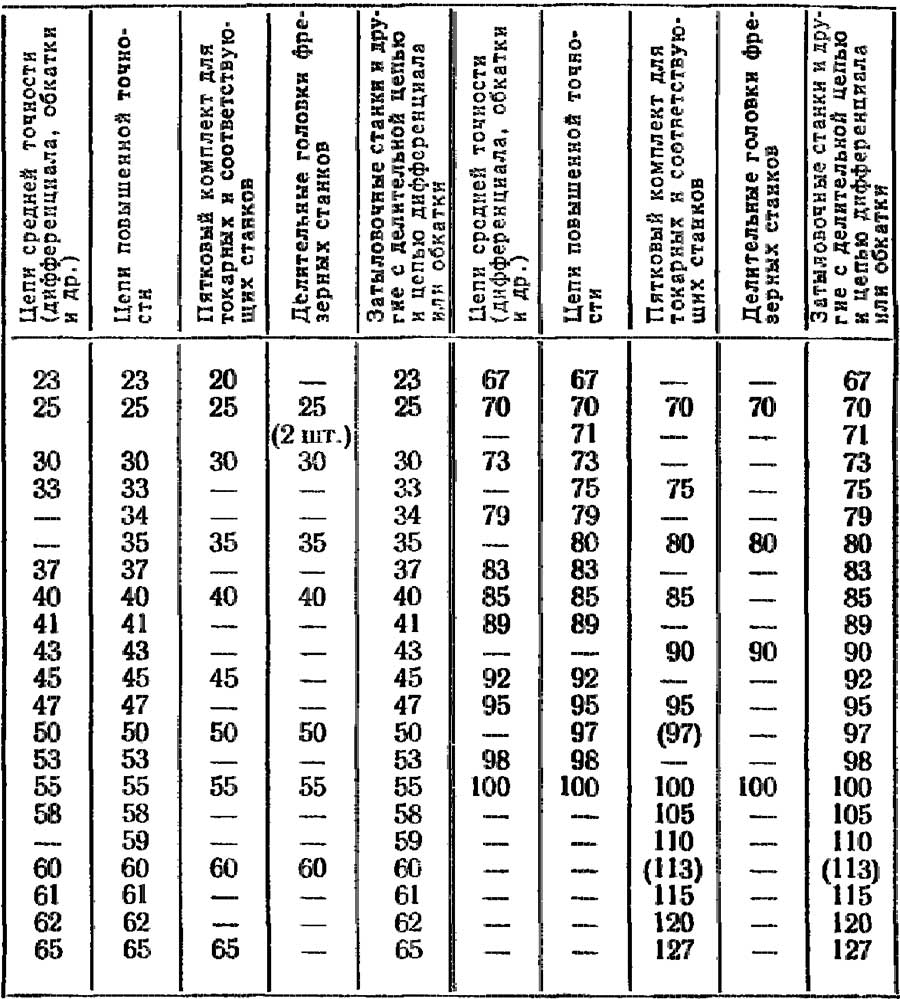
Для настройки делительных головок можно использовать таблицы, прилагаемые заводом. Сложнее, но можно выбирать подходящие пятковые комбинации из приводимых в данной книге «Основных таблиц для подбора зубчатых колес».

Расчет зубчатого колеса онлайн

Подпишитесь на нашу рассылку!

Geargenerator — онлайн конструктор зубчатого зацепления

Если вы попали на эту страницу, то наверняка знаете программу Gear Template Generator(подробнее о программе). Эта программа позволяет делать расчет параметров зубчатого зацепления. Gear Template Generator устанавливается локально на компьютер и позволяет создавать чертеж пары шестеренок с необходимыми параметрами. (Скачать Gear Template Generator можно тут)

Сейчас я расскажу о аналоге Gear Template Generator – онлайн конструкторе зубчатого зацепления Geargenerator. Собственно если вы введете в адресную строку браузера Geargenerator.com, то попадете на страницу конструктора.

Вот так выглядит начальное окно программы

Окно поделено на две части. Левая часть – панель настроек программы и шестеренок. На правой части будет отображаться результат.

Рассмотрим левую часть

Она условно разделена на несколько блоков с набором параметров. Рассмотрим эти блоки.

Самый верхний блок Animation – анимация движения шестеренок. Старт/стоп, сброс. Можно задать скорость вращения.

Далее идет блок Gears – это список шестеренок и работа с их количеством. По умолчанию там их четыре. Можно добавить, удалить или очистить. Причем новая шестеренка будет добавляться к той, которая выделена в данный момент.

Следующий блок настроек Connection properties – он отвечает за варианты стыковки шестеренок

Поле Parent gear #: — тут можно для текущей шестеренке указать номер родительской шестеренки(из списка Gears). По умолчанию самая первая шестеренка – нулевая. Таким образом можно быстро пере стыковать шестеренки.

Поле Axle connection: — определяет способ стыковки шестеренок. Если установить тут галочку – шестеренки будут стыковаться на одной оси.

Поле Connection angle : — указывает угол на центр шестеренки относительно родительской шестеренки.

Положение шестеренки #1 при значении Connection angle : – 60

Положение шестеренки #1 при значении Connection angle: – 85

Далее Gear properties – параметры самих шестеренок(количество зубьев, параметры зуба и т.д.) В этом же блоке есть самая главная кнопка — Download SVG – клик по ней начинает загрузку файла с шестеренками в формате SVG

Последний блок Display – настройки отображения самого конструктора. Можно поменять цветовую схему, включить/выключить сетку и метки на шестеренках.

Теперь небольшой пример работы

Уменьшим количество зубьев шестеренки #3 до 42

Добавим шестеренку #4 к шестеренке #3 (для этого в блоке Gears нужно кликнуть по #3, а затем по кнопке Add New)

Укажем для #4, что она должна располагаться на одной оси с #3

Добавим к #3 и #4 еще по одному зубчатому колесу с указанием параметра Connection angle (разведем их в стороны)

Нажмем кнопку Start/Stop – и посмотрим на анимацию. Таким образом можно не только собрать нужную последовательность передач, но и подобрать расположение осей шестеренок для дальнейшего размещения в корпусе изделия.

Резюме.

В этом онлайн конструкторе зубчатого зацепления можно выстроить почти весь механизм часов(то, что касается шестеренок). Можно строить достаточно сложные схемы соединения зубчатых колес. В отличие от Gear Template Generator, где можно строить только одну пару шестеренок. Но Gear Template Generator дает большую свободу в настройке параметров шетеренок.

GearGenerator позволяет экспортировать только в SVG.

GearGenerator работает онлайн, не требует установки и бесплатен.

Еще один плюс — все параметры созданного вами зубчатого зацепления добавляются в адресную строку. Сохранить или поделиться результатом своего конструирования можно скопировав текст адресной строки. Пример, который я описывал выше — результат можно увидеть по этой ссылке.

Обе программы обладают своими плюсами. Какую из них выбрать – выбор за вами.