Геометрические параметры конической зубчатой передачи

Конические зубчатые передачи. Устройство и основные геометрические и силовые соотношения

Зубчатую передачу с пересекающимися осями, у которой начальные и делительные поверхности колес конические, называют конической.

Коническая передача состоит из двух конических зубчатых колес (рис. 45) и служит для передачи вращающего момента между валами с пересекающимися осями под углом . Наиболее распространена в машиностроении коническая передача с углом между осями Z=90 0 (рис. 47), но могут быть передачи и с . Колеса конических передач. выполняют с прямыми (рис. 46, а), косыми (рис. 46, б), круговыми зубьями (рис. 46, в).

Рис. 45. Коническая пря­мозубая передача

Рис. 46. Конические зубчатые колеса: а — коле­со с прямыми зубьями;

б — колесо с косыми зу­бьями; в — колесо с круговыми зубьями

Рис. 47. Геометрические параметры конических зубчатых колес

Рис. 48. Гипоиднаяя передача

Передачу с коническими колесами для передачи вращающего момента между валами со скрещиваю­щимися осями называют гипоидной (рис. 48). Эта передача находит применение в автомобилях.

По стоимости конические передачи дороже ци­линдрических при равных силовых параметрах. Их применение диктуется только необходимостью пе­редавать момент при пересекающихся осях валов. Передаточное число одной пары .

Вершины начальных и делительных конусов конической передачи на­ходятся в точке пересечения осей валов О (рис. 50). Высота и толщина зубьев уменьшаются по направлению к вершинам конусов. Геометрические параметры конической передачи (рис. 47 и 50):

АОВ — делительный конус шестерни;

ВОС — делительный конус колеса;

АО₁В — делительный дополнительный конус шестерни;

ВО₂С — делительный дополнительный конус колеса;

— угол делительного конуса шестерни;

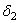— угол делительного конуса колеса;

d_e[ — внешний делительный диаметр шестерни;

d₁ — средний делительный диаметр шестерни;

b — ширина зубчатого венца (длина зуба);

R_e — внешнее делительное конусное расстояние (или длина дис­танции).

Рис. 50. Коническая прямозубая передача

Передаточное число конической передачи определяется так:

В конической передаче может быть бесчисленное множество делительных окружностей. Для расчета в машиностроении принимают внешнюю и среднюю делительные окружности (см. рис. 47).

Из условия, что в конической передаче модуль и делительный связаны теми же соотношениями, что и в цилиндрических передачах, т.е. d=mz (рис.51), определяют внешний d_e и средний d_m делительные метры:

где т_е — внешний окружной модуль; т_т — средний окружной модуль.

Рис. 51. Зуб конического колеса

Внешний окружной модуль обычно выбирают из стандартного ряда(см. табл. 3). Округление внешнего модуля до стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его значению определяют все геометрические параметры зубча­тыхколес (задают размеры зубьев на внешнем торце, на котором удобнопроизводить измерения).

Средний окружной модуль т рассчитывают в зависимости от внешнегоокружного модуля т_е. По среднему окружному модулю производят расчет передачи на прочность при изгибе.

Рис. 52

Зависимость между т_е и т_т в конической передаче.

Из рис. 3.51 ,где (из ). Отсюда .

Умножив левую и правую части равенства на два, получим . Разделив левую и правую части равенства на , получим

или

Геометрические соотношения размеров прямозубой конической пере­дачи с эвольвентным профилем зуба. Согласно рис. 53 внешний диаметр вершин зубьев

внешний диаметр впадин зубьев

Длина зуба (ширина венца) [ при условии и ,где 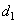— средний делительный диаметр шес­терни].

Рис. 53. Геометрия прямозубой конической передачи

Ориентировочно длина зуба может быть выбрана также в зависимости от внешнего делительного конусного расстояния R_e:

.

Таблица 17. Геометрические параметры прямозубой конической передачи

Геометрические параметры конической передачи

Конические зубчатые колёса применяют в передачах с пересекающимися осями под некоторым углом. Наиболее распространены передачи с углом ∑ = 90°. Нагрузочная способность конической передачи составляет около 85 % от цилиндрической. Различают конические передачи с прямыми, косыми (тангенциальными) и круговыми зубьями (рис. 19). Прямозубые конические колёса применяют при невысоких окружных скоростях как наиболее простые в монтаже (не более 8 м/c). Чаще применяют колёса с круговыми зубьями, которые обладают рядом преимуществ:

— при одинаковых габаритных размерах имеют более высокую несущую способность;

— обеспечивают более плавное зацепление и мéньшую шумность вследствие большого перекрытия зубьев в зацеплении.

При круговых зубьях преимущественно применяют β = 35°, при тангенциальных — β = 20 … 30° (кратно 5°).

Рис. 19. Конические колёса:

а) — с прямым зубом; б) — с косым зубом; в) — с круговым зубом

Вместо начальных и делительных цилиндров цилиндрических колёс вводят понятие начального и делительного конуса, которые, как правило, совпадают, так как модификацию (коррегирование) конических передач практически не применяют. В качестве торцовых сечений рассматривают сечения поверхностями дополнительных конусов, оси которых совпадают с осью колеса (внутренний и внешний торцовый конус, рис. 20).

Для удобства измерения конических колёс их размеры принято определять по внешнему торцовому конусу (геометрические параметры конического колеса, измеренные по внешнему торцовому конусу, имеют индекс — e). При расчёте диаметров колеса используют окружной (торцовый) m_е и нормальный m_n модули. Окружной модуль определяет внешний делительный диаметр d_e, нормальный — средний делительный диаметр d:

, . (3.6)

Для нормального зацепления высота головки и высота ножки зуба соответственно равны: h_ae = m_e , h_af = 1,2m_e .

Рис. 20. Геометрические параметры конического колеса

Внешний диаметр вершин зубьев равен:

, (3.7)

где δ — угол делительного конуса.

Рис. 21. Схема конической передачи

Передаточное отношение конической передачи (рис. 21) будет определяться отношением внешних делительных диаметров:

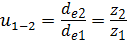. (3.8)

Учитывая, что , где R_e — внешнее конусное расстояние, то выражение для определения передаточного отношения можно записать в виде:

. (3.9)

, или .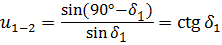

Таким образом, передаточное отношение конической передачи будет равно:

. (3.10)

Внешнее конусное расстояние:

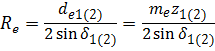. (3.11)

Среднее конусное расстояние R = R_e – 0,5b.

Детали машин

Конические зубчатые передачи

Общие сведения о конических зубчатых передачах

Конические зубчатые колеса применяют в передачах, когда оси валов пересекаются под некоторым углом Σ . Обычно это связано с необходимостью изменить направление передаваемого вращающего момента. Наибольшее распространение получили ортогональные конические передачи, изменяющие направление вращающего момента под прямым углом (угол Σ = 90˚, см. рис. 3).

Конические передачи подразделяются не только по углу пересечения валов и осей зубчатых колес. Они бывают с прямыми и круговыми (спиралевидными) зубьями. Встречаются и конические передачи, у которых колеса выполнены с шевронными зубьями, но из-за сложности изготовления такие передачи широкого практического применения не нашли.

Прямозубые конические передачи имеют начальный линейный контакт в зацеплении, а передачи с круговыми зубьями – точечный контакт.

Основными преимуществами зубчатых колес с круговыми зубьями являются бόльшая несущая способность, относительная бесшумность и плавность работы. Недостаток – они сложнее в изготовлении, а, следовательно, дороже.

Нарезание кругового зуба производят резцовыми головками по методу обкатки (рис. 1). Угол наклона зуба β_n в середине ширины зубчатого венца выбирают, учитывая плавность зацепления. Рекомендуется принимать β_n = 35˚.

Сопряженные колеса с круговым зубом имеют противоположное направление линий зубьев – правое и левое, если смотреть со стороны вершины конуса. Шестерни выполняют с правым зубом, колеса – с левым (рис. 1 ).

В конических передачах шестерню, как правило, располагают консольно (рис. 2), при этом вследствие меньшей жесткости консольного вала и деформаций опор увеличивается неравномерность распределения нагрузки пол длине контактных линий в зацеплении. По этой причине конические колеса по сравнению с цилиндрическими работают с большим шумом.
С целью снижения деформаций зубьев вал устанавливают на конических роликовых подшипниках, выдерживая соотношение l/l₁ = 2,5 (рис. 2). Подшипники располагают в стакане для обеспечения возможности осевого перемещения узла конической шестерни при регулировании зацепления.

Передаточное число конической зубчатой передачи может быть определено из соотношений:

где d_e1 , d_e2 и δ₁ , δ₂ – соответственно внешние делительные диаметры и углы делительных конусов шестерни и колеса.

Для конической прямозубой передачи рекомендуемые значения передаточного числа u = 2…3, при колесах с круговыми зубьями – до 6,3.

Геометрия зацепления колес

Аналогами начальных и делительных цилиндров цилиндрических зубчатых передач в конических передачах являются начальные и делительные конусы. При вращении колес начальные конусы катятся друг по другу без скольжения (рис .3). В конических передачах угловая модификация не применяется, поэтому начальные и делительные конусы всегда совпадают.

Угол Σ между осями зубчатых колес равен сумме углов делительных конусов: Σ = δ₁ + δ₂ .

Эвольвентные зубья конического колеса профилируют на развертке дополнительного конуса, образующая которого перпендикулярна образующей делительного конуса. Дополнительные конусы можно построить для внешнего, среднего и внутреннего сечений зуба конического колеса.
Ширина b венца зубчатого колеса ограничена двумя дополнительными конусами – внешним и внутренним.

Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют трех осевых форм (рис. 4).

Осевая форма I – нормально понижающиеся зубья.
Вершины делительного конуса и конуса впадин совпадают. Применяют для прямых зубьев, а также для круговых зубьев при m ≥ 2 мм и √(z₁ 2 + z₂ 2 ) = 20…100.

Осевая форма II – нормально сужающиеся зубья.
Вершина конуса впадин располагается так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу растет с увеличением расстояния от вершины. По этой форме одним инструментом можно обработать сразу обе поверхности зубьев колеса, что повышает производительность при нарезании зубчатых колес. Осевая форма II является основной для колес с круговыми зубьями. Применяют в массовом производстве.

Осевая форма III – равновысокие зубья.
Образующие конусов делительного, впадин и вершин параллельны. Высота зубьев постоянна по всей длине. Применяют для круговых зубьев при √(z₁ 2 + z₂ 2 ) ≥ 60 и для неортогональных передач с углом Σ 2 + z₂ 2 ) =
= 0,5 d_e2√(u 2 + 1)/u

Конические зубчатые передачи

Очень часто необходимо передавать вращательное движение с изменением направления. Для решения этой задачи разработан и успешно применяется специальный вид зубчатых передач. Они дали название целому классу таких механизмов — конические зубчатые передачи. Данные агрегаты способны обеспечить изменение направления вращения в широком диапазоне углов. Кроме изменения направления они способны изменять частоту оборотов и мощность.

Распространение получили передачи, которые способны изменять направление под прямым углом. Изменение направления производится перпендикулярно ведущей оси.

Устройство конической зубчатой передачи

Классическая схема подобных передач имеет в своём составе два вала. Один является ведущим, второй – ведомым. На каждом из них закреплены колёса, выточенные в форме конуса. Коническое зубчатое колесо обработано под заданным углом. В результате обработки получается зубчатое колесо с изменяемым диаметром от основания к вершине. Полученная фигура напоминает конус. На боковой поверхности вырезаны зубья. Итоговый угол направления вращения определяется суммой нескольких углов. Он складывается из углов обоих колёс которые изготовлены в форме конуса.

Общие сведения про конические зубчатые передачи включены в справочники по расчёту редукторов и мультипликаторов.

Закрепленное на валу колесо, с которого производится передача вращения, называется ведущим. Колесо, которому передаётся вращение, называется ведомым.

Подобные конструкции классифицируются по следующим показателям:

К механическим характеристикам относятся:

• форма передаточного механизма;
• форме применяемых зубьев;
• количеству ступеней;
• направление пересечения осей;
• нагрузочная способность;
• значение передаточного числа;
• прочность при изгибе;
• величина усилия в зацеплении;
• передаваемая мощность.

К характеристикам, определяющим геометрическую форму применяемых колёс, шестерёнок, валов относятся значения углов и линейные размеры отдельных частей деталей.

По форме механизма передачи бывают:

• чисто конические;
• цилиндрические конические;
• конические линейные.

Формы зубьев и способам зацепления устройства изготавливаются следующих видов:

• прямоугольной формы (прямозубое);
• зубьями на скос, которые получили название косозубые;
• округлой формы;
• в форме спирали с постоянным шагом;
• эвольвентные;
• циклоидные;

При внешнем зацеплении шестерни вращаются в противоположных направлениях. Во втором случае вращение происходит в одном направлении.

Важным параметром является показатель круговой скорости вращения. Они подразделяются:

• с низкой скоростью (так называемые тихоходные, у которых скорость вращения не превышает 3 м/с);
• среднескоростные (скорость которых достигает 15 м/с);
• высокоскоростные (для них допускается превышение скорости 15 м/с).

Конструкция подобных механизмов бывает одноступенчатая и многоступенчатая. Схема передачи выполняется с преобразованием характера движения или без него. В первом случае вращательное движение сохраняется на выходе передаточного механизма. Во втором случае оно может быть преобразовано из вращательного движения в поступательное движение.

По форме касательных линий нарезанных зубьев выделяют следующие виды шестерён:

• С зубьями, боковое ребро которых представляет прямую линию. Линия зуба у них всегда проходит через вершину делительного конуса;
• У круговых зубьев угол наклона при обработке делается острым. Он получил название линия конуса и измеряется между касательной к выбранной точке и линией самого зуба.

Широко распространённым в таких механизмах является эвольвентное зацепление. При такой форме зацепления происходит перекатывание поверхности ведущего зуба по образующей плоскости ведомого колеса.

Серьёзным недостатком всех конических передач является большие массогабаритные характеристики. Еще одной трудностью является проблема обработки. На конусе, который получен в качестве заготовки будущей шестерёнки значительно сложнее нарезать зубья. Если в кинематической схеме нет элементов с пересекающимися осями, такие механизмы называются гипоидными.

Дальнейшее развитие получили варианты не только с прямыми, но и криволинейными зубьями: круговыми, эвольвеньными, циклоидной формы.

В некоторых устройствах применяется коническая зубчатая передача, у которой колёса имеют прямые зубьями с радиальной нарезкой или нарезкой в форме спирали. Все эти типы применяются для решения конкретных технических задач.

При проектировании расчёт основных технических характеристик, определяющих параметры редуктора, производится с использованием известных выражений. Полученные значения подтверждаются результатами проведенных экспериментов, испытаний, и эксплуатационных данных. Например, опытным путём было установлено, что нагрузочная способность любой конической передачи ниже, чем у цилиндрической. Поэтому при расчёте применяют специальный коэффициент, учитывающий это снижение.

Передаточное отношение определяет, к какому классу относится данный вид механизма. Если передаточное число конической передачи меньше единицы – конструкция понижающая (редуктор). Если этот показатель больше или равен единице – повышающая (мультипликатор).

Он рассчитывается как отношение угловых скоростей на ведомом валу по отношению к ведущему валу.

Криволинейные зубья на шестерёнках конических передач обладают более высокими нагрузочными характеристиками. Работают плавно без рывков и проскальзываний. Это снижает общие динамические нагрузки и уровень шума.

Разработанными стандартами определены величины допусков. Они имеют двенадцать ступеней точности. Каждая из степеней зависит от скорости передаваемого вращения. Разрешенные круговые скорости имеют следующие значения:

• до 6-й степени точности включительно скорость может достигать 20 м/с;
• для 7-й степени этот параметр не должен превышать 10 м/с;
• 8-я степень допускает передачу на скоростях до 7 м/с;
• у девятой и выше скорости не должны превышать 3 м/с.

Основные геометрические параметры

Построение кинематической схемы, технические характеристики, способы обработки отдельных деталей этих механизмов задаются геометрической формой отдельных элементов. Основными геометрическими параметрами, которые рассчитываются при проектировании являются:

• углы делительных конусов (каждого колеса или шестерёнки);
• диаметры всех элементов (обоих валов, ведущих и ведомых шестерён);
• внешний окружной модуль шестерни;
• расстояние от вершины конуса до его образующей (называется делительное расстояние);
• расстояние между осей;
• радиальный зазор применяемых подшипников;
• делительный диаметр (он определяет величину зуба шестерёнки);
• диаметр углублений и верхней части зубьев.

Для удобства проведения расчетов и понимания механизма зацепления вводят три вида торцовых сечений. Это сечения во внешней, внутренней и средней части каждого зуба.

Уменьшение толщины зубьев по направлению к вершине приводит к созданию надежного зацепления во время движения. Угол наклона по направлению к вершине определяет параметры, задаваемые при обработке.

Под линией зубьев понимают пересечение двух прямых. Одна образована боковой поверхностью зуба, вторая является краем делительной конической поверхности.

Для улучшения эксплуатационных характеристик — повышения износостойкости, сопротивления при контакте, уменьшение заедания и лучшей передачи коническим зубчатым колёсам энергии вращения используют метод выравнивания коэффициентов удельного скольжения.

С этой целью колесо и шестерню стараются изготовить с одинаковыми параметрами смещения, но с разными знаками. Например, для шестерни задают параметр со знаком плюс, а для колеса со знаком минус.

Основные геометрические соотношения задаются на этапе разработки всего механизма конической передачи качество передачи. Геометрические параметры рассчитываются на основании известных соотношений.

Усилия в зацеплении

Обеспечение высокой надёжности работы, точности передачи крутящего момента производится благодаря правильному расчету параметров всех сил, которые оказывают воздействие на механизм в процессе работы. Коническая зубчатая передача подвержена воздействию одновременно нескольких сил.

Суммарный результирующий вектор всех сил складывается из отдельных составляющих.

Сила, обеспечивающая нормальное зацепление зубьев называется силой нормального давления.

Она складывается из трёх составляющих. Окружной силы, осевой и радиальной.

Величина каждой из составляющих вычисляется по классическим физическим выражениям. Они приведены в справочниках по расчёту зубчатых передач. Каждое из расчетных выражений учитывает специфику соединений, размеры механизма, параметры зацепления.

Для предотвращения эффекта заклинивания зубьев во время зацепления необходимо произвести точную оценку величины силы направленной вдоль оси вала. Другая осевая сила направлена от вершины зуба, то есть конуса к центру. Направление и скорость вращения обоих типов колёс (ведущего и ведомого) определяет направление воздействия так называемых окружных сил.

Вектор сил, имеющий радиальную направленность, стремится к осям на которых вращаются колёса.

Достоинства и недостатки

Применение данной кинематической схемы наглядно показало наличие преимуществ.

К положительным моментам можно отнести:

• способность изменять направление передаваемого движения;
• широкая область применения;
• эффективно реализована передача, преобразование, увеличение мощности вращательного движения между осями передачи расположенными под углом друг к другу;
• достаточно широкий диапазон задания углов передачи крутящего момента от ведущего элемента к ведомому;
• широкая вариативность при компоновке разрабатываемых зубчатых и комбинированных систем;
• высокие нагрузочные характеристики (данные устройства способны передавать мощность величиной до 5000 кВт);
• эксплуатация и обслуживание не вызывает трудностей;
• удаётся получить высокий КПД.

К недостаткам специалисты причисляют:

• нагрузочная способность ниже, чем у цилиндрических конструкций (в среднем она на 20 процентов ниже);
• невысокая несущая способность (этот показатель ниже на 15 процентов);
• сложность и трудоёмкость в изготовлении колёс с заданными параметрами зубьев (количеством, величиной, углом наклона);
• повышенные требования к точности нарезания зубьев;
• возникновение повышенных осевых и изгибных нагрузок на все валы (особенно этот эффект наблюдается между валами, расположенными консольно);
• необходимость регулировки процесса передачи вращения;
• обладают большей массой, чем другие зубчатые передачи;
• высокие затраты на производство и обслуживание;
• возникают трудно разрешимые проблемы при проектировании и изготовлении систем с изменяемым передаточным числом;
• повышенная общая жёсткость конструкции.

Применение механизма

Область применения подобных передач целесообразно рассматривать по трём наименованиям: скоростные, силовые, приборные. Все они получили широкое распространение в различных отраслях промышленности. Зубчатые колёса хорошо зарекомендовали себя при создании самых сложных кинематических схем.

Скоростные передачи предназначены для повышения скорости передаваемого вращения. Они успешно применяются в редукторах турбомашин, коробках перемены передач автомобилей (механических и автоматических).

От силовых передач требуется значительное повышение мощности передаваемого вращения. Они эксплуатируются в крановых установках, прокатных станах, тяговых механизмах различного назначения. Такие конструкции работают на малых скоростях. Благодаря этому удаётся передавать большие крутящие моменты. Главным требованием, которое предъявляют к элементам таких систем – плотный контакт между зубьями входящими в зацепление.

На практике распространение получил класс гипоидных агрегатов. Их устанавливают в механизмы и оборудование которые, используются в общем машиностроении. Например, грузовых и легковых автомобилях (в качестве элементов трансмиссии). Особое место такие системы занимают в вертолётостроении. Их применяют на летательных аппаратах практически всех конструкций. Этого удалось добиться благодаря применению зубчатых колёс оснащённых круговыми зубьями. Увеличением угла наклона зуба позволяет передаче работать более плавно. В этом случае удаётся избавиться от рывков и проскальзываний. Наиболее эффективным считается угол т равный 35°. Такие колеса обладают повышенной несущей способностью, надёжностью и долговечностью. Данные передачи работают плавно и практически бесшумно. Они надёжно выполняют свои функции, даже на высоких скоростях. Эта способность реализована благодаря многопарному зацеплению. Такой механизм позволяет снизить динамические нагрузки и предотвратить проскальзывание. Конструкции подобного вида активно применяются в приводе несущих винтов вертолетов различных аэродинамических схем.

Приборные или отсчетные устройства применяют в механизмах научно — исследовательских приборов, счетно-решающих устройствах, бытовой технике. Ведущие и ведомые элементы в этих устройствах могут изготавливаться из цветных металлов или синтетических и полимерных материалов.

Основным требованием к коническим системам в таких агрегатах является соблюдение высочайшей кинематической точности при изменении направления вращения.

В ней должны быть хорошо согласованы углы наклона ведущего и ведомого колеса, точно выверен угол поворота.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Геометрические параметры конических зубчатых передач

Геометрические расчеты конических колес аналогичны расчетам цилиндрических. Зубья конических колес образуются обкатыванием по плоскому колесу с прямолинейным профилем зубьев аналогично тому, как зубья цилиндрических колес образуются обкатыванием по рейке. Число зубьев плоского колеса (может получиться дробным). Вместо начальных и делительных цилиндров цилиндрических колес в конических колесах вводятся понятия: начальный и делительный конусы, которые, как правило, совпадают, так как для конических колес угловую коррекцию практически не применяют. В качестве торцовых сечений рассматривают сечения поверхностями дополнительных конусов, т.е. Конусов, оси которых совпадают с осью колеса, а образующие перпендикулярны к образующим делительного конуса. Используются понятия внешнего и внутреннего дополнительных конусов (ограничивающих зубчатый венец) и среднего дополнительного конуса. Действительные профили зубьев конических колес весьма близки к профилям воображаемых эквивалентных цилиндрических колес с радиусами делительных окружностей, равными длинам образующих дополнительных конусов. Зубья конических колес по признаку изменения размеров сечений по длине выполняют трех форм.

Осевая форма I — нормально понижающиеся зубья; вершины делительного и внутреннего конусов совпадают (а). Эту форму применяют для конических передач с прямыми и тангенциальными зубьями, а также ограничено для передач с круговыми зубьями при и .

Осевая форма II(б) — вершина внутреннего конуса располагается так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу растет с увеличением расстояния от вершины. Эта форма позволяет обрабатывать одним инструментом сразу обе поверхности зубьев колеса. Поэтому она является основной для колес с круговыми зубьями, широко применяется в массовом производстве.

Осевая форма III (в) — равновысокие зубья; образующие делительного и внутреннего конусов параллельны. Эту форму применяют для круговых зубьев при , в частности при средних конусных расстояниях 75—750 мм. Формы II и III получают смещением вершины конуса впадин и вершины делительного конуса (б, в). Области применения подробнее см. ГОСТ 19326—73.

У конических колес удобно измерять, а потому и задавать размеры зубьев на внешнем дополнительном конусе. В зубчатых колесах с зубьями формы I обычно оперируют окружным модулем на внешнем торце. В зубчатых колесах с зубьями формы II и III преимущестенно оперируют нормальным модулем на середине ширины зубчатого венца. Круговые зубья нарезают немодульным инструментом, позволяющим обрабатывать зубья в некотором диапазоне модулей. Поэтому допускается применять передачи с нестандартными и дробными модулями.

Соотношение между модулями и следующее:

где — внешнее конусное расстояние Угол наклона линии зуба выбирают, учитывая, что увеличение улучшает плавность зацепления, но при этом возрастают усилия. При круговых зубьях преимущественно применяют = 35°, а при тангенциальных 20. 30°, обычно угол выбирают кратным 5°. Минимально допустимые числа зубьев приведены в таблице:

Для уменьшения шума рекомендуют применять притирку и выбирать некратные числа зубьев колес. Для зубчатых передач с твердостью рабочих поверхностей зубьев шестерни и колеса число зубьев шестерни рекомендуют выбирать по следующим графикам в зависимости от внешнего делительного диаметра шестерни , при твердости и 2,5 удобно применять так называемую тангенциальную коррекцию, заключающуюся в утолщении зуба шестерни и соответственном утонении зуба колеса. Тангенциальная коррекция конических колес не требует специального инструмента, так как ее получают благодаря разведению резцов, обрабатывающих противоположные стороны зубьев. Для цилиндрических колес тангенциальную коррекцию не применяют, так как она требует специального инструмента. Основные размеры конических зубчатых колес с прямыми, тангенциальными и круговыми:

РАСЧЕТ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС

На основании формул (3.4) и (3.5) с учетом особенности геометрии конических зубчатых колес (рис. 3.4) после соответствующих преобразований получают формулу для проверочного расчета конических прямозубых колес на контактную прочность:

Рис. 3.4. Схема передачи коническими зубчатыми колесами

При расчете по среднему конусному расстоянию R = Re — 0,5b формула (3.27) принимает вид

Здесь R_e и R — внешнее и среднее конусные расстояния, мм; К_н — коэффициент нагрузки, принимаемый таким же, как и для цилиндрических прямозубых передач (см. § 3.2), при условии, что степень точности конических колес на единицу выше, чем цилиндрических; Т₂ — вращающий момент на колесе, Н • мм; b — ширина зубчатого венца, мм.

Аналогичный расчет для конических колес с круговыми зубьями основывается на формулах (3.4) и (3.6). Рекомендуют принимать средний угол наклона зуба р = 35° (рис. 3.5). При этом коэффициент, учитывающий формулу сопряженных поверхностей зубьев, Z_H= 1,59. Коэффициент Z_? можно принять таким же, как и для цилиндрических косозубых колес, т.е. Z_e = 0,8. Тогда для проверочного расчета стальных конических колес с круговыми зубьями на контактную прочность формула будет иметь вид

Коэффициент нагрузки /^представляет собой произведение трех частных коэффициентов, определяемых так же, как и для цилиндрических косозубых колес:

Рис. 3.5. Схема конического колеса с круговыми зубьями

При проектировочном расчете определяют внешний делительный диаметр колеса, мм:

для прямозубых передач К = 99; для колес с круговыми зубьями K_d= 86.

Полученные значения d_e2 округляют по ГОСТ 12289-76 (в мм): 50; (56); 63; (71); 80; (90); 100; (112); 125; (140); 160; (180); 200; (225); 250; 280; 315; 355; 400; 450; 500; 560; 630; 710; 800; 900; 1000; 1120; 1250; 1400; 1600.

Предпочтительными являются значения без скобок.

Фактические значения d_e2 не должны отличаться от номинальных более чем на 2%.

Номинальные значения передаточных чисел и желательно округлить по ГОСТ 12289-76:1; (1,12); 1,25; (1,40); 1,60; (1,80); 2,00; (2,24); 2,50; (2,80); 3,15; (3,55); 4,00; (4,50); 5,00; (5,60); 6,30.

Значения без скобок предпочтительнее.

Фактические значения и не должны отличаться от номинальных более чем на 3%.

Коэффициент ширины зубчатого венца

При проектировании редукторов с параметрами по ГОСТ 12289—76 рекомендуется принимать f_bRg = 0,285.

Коэффициент Кщ принимают предварительно для колес с твердостью поверхностей зубьев НВ 350 — от 1,25 до 1,45 (см. табл. 3.1).

При проверочном расчете значения коэффициента нагрузки уточняют.

Далее определяют числа зубьев колес. Для шестерни

Рекомендуют выбирать z _<

Число зубьев колеса z₂ = Так как найденные значения z, и z₂

округляют до целых чисел, то после этого следует уточнить и = z₂/z_y и угол 8₂ = arctgw. Внешний окружной модуль т_е = djz <,округлять полученное значение т_е не обязательно.

Остальные параметры передачи определяют по табл. 3.11.

Таблица 3.11. Конические прямозубые колеса по ГОСТ 19325-73 и ГОСТ 19624-74 (при 8₁ + 6₂ = 90° и а = 20°)