Что обозначает класс точности прибора

Что означает класс точности измерительного прибора

Класс точности измерительного прибора — это обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых установлены в стандартах на отдельные виды средств измерений. Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых при помощи этих средств.

Для того чтобы заранее оценить погрешность, которую внесет данное средство измерений в результат, пользуются нормированными значениями погрешности . Под ними понимают предельные для данного типа средства измерений погрешности.

Погрешности отдельных измерительных приборов данного типа могут быть различными, иметь отличающиеся друг от друга систематические и случайные составляющие, но в целом погрешность данного измерительного прибора не должна превосходить нормированного значения. Границы основной погрешности и коэффициентов влияния заносят в паспорт каждого измерительного прибора.

Основные способы нормирования допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ.

На шкале измерительного прибора маркируют значение класса точности измерительного прибора в виде числа, указывающего нормированное значение погрешности. Выраженное в процентах, оно может иметь значения 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001 и т. д.

Если обозначаемое на шкале значение класса точности обведено кружком, например 1,5, это означает, что погрешность чувствительности δ s =1,5%. Так нормируют погрешности масштабных преобразователей (делителей напряжения, измерительных шунтов, измерительных трансформаторов тока и напряжения и т. п.).

Это означает, что для данного измерительного прибора погрешность чувствительности δ s= d x/x — постоянная величина при любом значении х. Граница относительной погрешности δ (х) постоянна и при любом значении х просто равна значению δ s, а абсолютная погрешность результата измерений определяется как d x= δ sx

Для таких измерительных приборов всегда указывают границы рабочего диапазона, в которых такая оценка справедлива.

Если на шкале измерительного прибора цифра класса точности не подчеркнута, например 0,5, это означает, что прибор нормируется приведенной погрешностью нуля δ о=0,5 %. У таких приборов для любых значений х граница абсолютной погрешности нуля d x= d о=const, а δ о= d о/хн.

При равномерной или степенной шкале измерительного прибора и нулевой отметке на краю шкалы или вне ее за хн принимают верхний предел диапазона измерений. Если нулевая отметка находится посредине шкалы, то хн равно протяженности диапазона измерений, например для миллиамперметра со шкалой от -3 до +3 мА, хн= 3 — (-3)=6 А.

Однако будет грубейшей ошибкой полагать, что амперметр класса точности 0,5 обеспечивает во всем диапазоне измерений погрешность результатов измерений ±0,5 %. Значение погрешности δ о увеличивается обратно пропорционально х, то есть относительная погрешность δ (х) равна классу точности измерительного прибора лишь на последней отметке шкалы (при х = хк). При х = 0,1хк она в 10 раз больше класса точности. При приближении х к нулю δ (х) стремится к бесконечности, то есть такими приборами делать измерения в начальной части шкалы недопустимо.

На измерительных приборах с резко неравномерной шкалой (например на омметрах) класс точности указывают в долях от длины шкалы и обозначают как 1,5 с обозначением ниже цифр знака «угол».

Если обозначение класса точности на шкале измерительного прибора дано в виде дроби (например 0,02/0,01), это указывает на то, что приведенная погрешность в конце диапазона измерений δ прк = ±0,02 %, а в нуле диапазона δ прк = -0,01 %. К таким измерительным приборам относятся высокоточные цифровые вольтметры, потенциометры постоянного тока и другие высокоточные приборы. В этом случае

δ (х) = δ к + δ н (хк/х — 1),

где хк — верхний предел измерений (конечное значение шкалы прибора), х — измеряемое значение.

Класс точности

Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.

Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.

Класс точности измерительного прибора

Обобщающая характеристика, которая определяется пределами погрешностей (как основных, так и дополнительных), а также другими влияющими на точные замеры свойствами и показатели которых стандартизированы, называется класс точности измерительного аппарата. Класс точности средств измерений дает информацию о возможной ошибке, но одновременно с этим не является показателем точности данного СИ.

Средство измерения – это такое устройство, которое имеет нормированные метрологические характеристики и позволяет делать замеры определенных величин. По своему назначению они бывают примерные и рабочие. Первые используются для контроля вторых или примерных, имеющих меньший ранг квалификации. Рабочие используются в различных отраслях. К ним относятся измерительные:

• приборы;
• преобразователи;
• установки;
• системы;
• принадлежности;
• меры.

На каждом средстве для измерений имеется шкала, на которой указываются классы точности этих средств измерений. Они указываются в виде чисел и обозначают процент погрешности. Для тех, кто не знает, как определить класс точности, следует знать, что они давно стандартизованы и есть определенный ряд значений. Например, на устройстве может быть одна из следующих цифр: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001. Если это число находится в круге, то это погрешность чувствительности. Обычно ее указывают для масштабных преобразователей, таких как:

• делители напряжения;
• трансформаторы тока и напряжения;
• шунты.

Обозначение класса точности

Обязательно указывается граница диапазона работы этого прибора, в пределах которой значение класса точности будет верно.

Те измерительные устройства, которые имеют рядом со шкалой цифры: 0,05; 0,1; 0,2; 0,5, именуются как прецизионные. Сфера их применения – это точные и особо точные замеры в лабораторных условиях. Приборы с маркировкой 1,0; 1,5; 2,5 или 4,0 называются технические и исходя из названия применяются в технических устройствах, станках, установках.

Возможен вариант, что на шкале такого аппарата не будет маркировки. В такой ситуации погрешность приведенную принято считать более 4%.

Если значение класса точности устройства не подчеркнуто снизу прямой линией, то это говорит о том, что такой прибор нормируется приведенной погрешностью нуля.

Грузопоршневой манометр, класс точности 0,05

Если шкала отображает положительные и отрицательные величины и отметка нуля находится посередине такой шкалы, то не стоит думать, что погрешность во всем диапазоне будет неизменной. Она будет меняться в зависимости от величины, которую измеряет устройство.

Если замеряющий агрегат имеет шкалу, на которой деления отображены неравномерно, то класс точности для такого устройства указывают в долях от длины шкалы.

Возможны варианты измерительных аппаратов со значениями шкалы в виде дробей. Числитель такой дроби укажет величину в конце шкалы, а число в знаменателе при нуле.

Нормирование

Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й

Нормирование осуществляется по:

Формулы расчета абсолютной погрешности по ГОСТ 8.401

Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.

Скачать ГОСТ 8.401-80

Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.

Виды маркирования

Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.

Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.

Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.

Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.

Пределы

Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.

Базовый способ определения погрешности

При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.

Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.

Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.

Класс точности 2,5

Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.

Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.

Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.

Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.

Пример расчета погрешности

Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.

Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.

Классы точности болтов

Болты и другие крепежные изделия изготавливают нескольких классов:

Каждый из них имеет свои допуски измеряемой величины, отличные от остальных и применяется в различных сферах.

Крепеж С используют в отверстиях с диаметром немногим больше диаметра болта (до 3мм). Болты без труда устанавливаются, не отнимая много времени на работу. Из минусов стоит отметить то, что при физическом воздействии на такой крепеж, болтовое соединение может сместиться на несколько миллиметров.

Крепеж В подразумевает использование болтов, диаметр которых меньше отверстия в пределах 1-1,5 мм. Это позволяет конструкции меньше подвергаться смещениям и деформациям, но повышаются требования к изготовлению отверстий в креплениях.

Гайки шестигранные класса точности В

Крепеж А создается по проекту. Диаметр болта такого типа, меньше диаметра отверстия максимум на 0,3 мм и имеет допуск только со знаком минус. Это делает крепеж неподвижным, не позволяет происходить смещению узлов. Изготовление болтов А-класса стоит дороже и не всегда используется в производстве.

Класс точности присутствует в описании всех измерительных приборов и является одной из самых важных характеристик. Чем выше его значение, тем более дорогостоящий будет прибор, но в то же время он сможет предоставить более точную информацию. Выбор стоить делать исходя из сложившейся ситуации и целей в которых будет использоваться такое средство. Важно понимать, что в некоторых ситуациях экономически выгодно будет приобрести дорогостоящее сверхточное оборудование, чтобы в дальнейшем сберечь деньги.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Обозначение класса точности

Практическое занятие № 6 КЛАССЫ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ

Учет всех метрологических характеристик средств измерений – сложная процедура, оправданная при измерениях высокой точности в метрологической практике. На производстве, как правило, такая точность не нужна. Большинство измерений являются однократными, поэтому за их результат принимается то значение величины, которое непосредственно снято с прибора (без обработки и оценивания погрешности, так как в этом нет необходимости). Но это не означает, что погрешности результатов данного вида измерений неизвестны. Они регламентируются заранее (до выполнения измерений) выбором необходимых по точности средств измерений. Поэтому для средств измерений, используемых в повседневной практике, принято деление по точности на классы.

Общие положения

Класс точности

Класс точности – обобщенная характеристика всех средств измерений данного типа, обеспечивающая правильность их показаний и устанавливающая оценку снизу точности показаний.

В стандартах на средства измерений конкретного типа устанавливаются требования к метрологическим характеристикам, в совокупности определяющие класс точности средств измерений этого типа. Например, у плоскопараллельных концевых мер длины такими характеристиками являются пределы допускаемых отклонений от номинальной длины и плоскопараллельности; пределы допускаемого изменения длины в течение года.

Устанавливая класс точности, нормируют пределы допускаемой основной погрешности. Ее дольные значения принимают в качестве пределов допускаемых дополнительных погрешностей.

Пределы допускаемых погрешностей выражают в форме абсолютных, приведенных или относительных погрешностей. Это зависит от характера изменения погрешности (в пределах диапазона измерений), назначения и условий применения средств измерений.

Если погрешность результатов измерений выражают в единицах измеряемой величины (например, при измерении длины, массы), то пределы допускаемых погрешностей выражают в форме абсолютных погрешностей.

Если границы абсолютных погрешностей средств измерений остаются практически неизменными, применяют форму приведенных погрешностей, если же эти границы нельзя считать постоянными – форму относительных погрешностей.

Абсолютная погрешность прибора

Абсолютная погрешность прибора (меры) Δ – разность между показанием прибора x_ПР (номинальным значением меры) и истинным значением измеряемой (воспроизводимой) x величины:

Пределы допускаемой абсолютной основной погрешности Δ устанавливают в зависимости от характера изменения погрешности в диапазоне измерений. Если погрешности не зависят от значения измеряемой величины x, то нормируют только границы:

где a – положительное число, не зависящее от x.

Если же с увеличением x погрешность возрастает линейно, то ее пределы устанавливают по формуле

где Δ – пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы;

x – значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале;

a, b – положительные числа, не зависящие от x.

Например, для генератора низкой частоты Г3-36: Δ = ±(0,03f + 2) Гц, где f – значение частоты.

Относительная погрешность

Относительная погрешность δ – отношение абсолютной погрешности Δ к значению измеряемой величины x:

. (18)

Пределы допускаемой относительной основной погрешности δ, если границы абсолютных погрешностей Δ можно полагать практически неизменными, находят по формуле

, (19)

Если границы абсолютных погрешностей Δ можно полагать меняющимися линейно, пределы допускаемой относительной основной погрешности δ находят по формуле

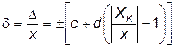, (20)

где δ – пределы допускаемой относительной основной погрешности, %;

q – отвлеченное положительное число, выбираемое из ряда, аналогичному ряду для p;

X_K – больший (по модулю) из пределов измерений;

c, d – положительные числа, выбираемое из ряда, аналогичному ряду для p;

c = b + d; . (21)

При постоянной абсолютной погрешности Δ (16) (рисунок 35, штриховые линии) относительная погрешность δ (18) убывает в гиперболической зависимости от измеряемой величины x (рисунок 36, штриховые линии). Если абсолютная погрешность Δ линейно увеличивается с ростом измеряемой величины x, например, по уравнению (17) (рисунок 35, сплошные линии), относительная погрешность δ (18) также убывает по гиперболической зависимости, но гипербола имеет более высокую кривизну (рисунок 36, сплошные линии).

При выборе прибора для измерений следует учитывать, что при постоянной абсолютной погрешности Δ на различных отметках шкалы будут соответствовать разные значения относительной погрешности δ (см. рисунки 35 и 36).

Пример

Для вольтметра со шкалой 0-150 В класса точности 1,5 основная предельная абсолютная погрешность Δ равна 2,25 В. Относительная погрешность δ (%), на отметках шкалы 25 и 100 В будет соответственно

С целью уменьшения относительной погрешности δ надо выбирать верхний предел шкалы измерительного прибора таким, чтобы ожидаемое значение измеряемой величины (показание) находилось в последней трети (или половине) ее.

Приведенная погрешность

Указание абсолютной Δ погрешности или относительной δ не позволяет сравнивать между собой по точности приборы с разными диапазонами измерений X_K. Поэтому для электроизмерительных приборов, манометров, приборов измерения физико-химических величин и др. характеристикой точности служит приведенная погрешность γ.

Приведенная погрешность γ – отношение абсолютной погрешности Δ к нормирующему значению X_N, в качестве которого выбирают верхний предел или диапазон измерений, длину шкалы и т.д.

, (22)

где γ – пределы допускаемой приведенной основной погрешности, %;

Δ – пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (1);

X_N – нормирующее значение, выраженное в тех же единицах, что и Δ;

p – отвлеченное положительное число, выбираемое из ряда 1·10 n ; 1,5·10 n ; (1,6·10 n ); 2·10 n ; 2,5·10 n ; (3·10 n ); 4·10 n ; 5·10 n ; 6·10 n (n = 1, 0, –1, –2 и т.д.).

Нормирующее значение X_N определяется, исходя из вида шкалы измерительного прибора:

1) шкала равномерная, практически равномерная или степенная – если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, нормирующее значение X_N устанавливают равным большему из пределов измерений или равным большему из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений;

2) шкала электроизмерительного прибора равномерная, практически равномерная или степенная и нулевой отметкой внутри диапазона измерений – нормирующее значение X_N устанавливают равным сумме модулей пределов измерений;

3) шкала с условным нулем (например, термометр с пределами измерений от 5 до 50 °С) – нормирующее значение X_N устанавливают равным модулю разности пределов измерений;

4) шкала существенно неравномерная – нормирующее значение X_N устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений.

Выражение пределов допускаемой погрешности в форме приведенных γ и относительных δ погрешностей является предпочтительным, так как они позволяют выражать пределы допускаемой погрешности числом, которое остается одним и тем же для средств измерений одного уровня точности, но с различными верхними пределами измерений.

Обозначение класса точности

В связи с большим разнообразием средств измерений и их метрологических характеристик ГОСТ 8.401-80 «Государственная система обеспечения единства измерений. Классы точности средств измерений. Общие требования» определены способы обозначения классов точности. Выбор способа зависит от того, в каком виде нормирована погрешность средства измерения. Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 8.

Для средств измерений, пределы допускаемой основной погрешности которых выражают в форме приведенной γ или относительной δ погрешности, классы точности обозначают числами, равными этим пределам в процентах. Чтобы отличить относительную погрешность δ от приведенной γ, на средстве измерений ее обводят кружком (см. таблицу 8). С той же целью под обозначением класса точности на средства измерений ставят знак “V” – это значит, что в случае обозначения приведенной погрешности γ предел абсолютной погрешности Δ приведен к длине шкалы или к ее части (X_N), а не к номинальной точке шкалы.

Таблица 8 – Правила построения и примеры обозначения классов точности в документации и на средствах измерений по ГОСТ 8.401-80

Что обозначает класс точности прибора

По приведенной погрешности (по классу точности) приборы делятся на восемь классов: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Приборы класса точности 0,05; 0,1; 0,2; 0,5 применяются для точных лабораторных измерений и называются прецизионными (от англ. precision – точность). В технике применяются приборы классов 1,0; 1,5: 2,5 и 4,0 (технические).

Класс точности прибора указывается на шкале прибора. Если на шкале такого обозначения нет, то данный прибор внеклассный, то есть его приведенная погрешность превышает 4%.Производитель, выпускающий прибор, гарантирует относительную погрешность измерения данным прибором, равную классу точности (приведенной погрешности) прибора при измерении величины, дающей отброс указателя на всю шкалу. Определив по шкале прибора класс точности и предельное значение, легко рассчитать его абсолютную погрешность ΔX = ± гX_пр / 100%, которую принимают одинаковой на всей шкале прибора. Знаки «+» и «–» означают, что по-грешность может быть допущена как в сторону увеличения, так и в сторону уменьшения от действительного значения измеряемой величины.

При использовании приборов для конкретных измерений редко бывает так, чтобы измеряемая величина давала отброс стрелки прибора на всю его шкалу. Как правило, измеряемая величина меньше. Это увеличивает относительную погрешность измерения. Для оптимального использования приборов их подбирают так, чтобы значения измеряемой величины приходились на конец шкалы прибора, это уменьшит относительную погрешность измерения и приблизит ее к классу точности прибора. В тех случаях, когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены наименьшего деления.

Класс точности – это характеристика прибора, которая определяется границами допускаемых основной и дополнительной погрешностей, а также другими свойствами, предусмотренными стандартами на данный вид изделия, которые оказывают влияние на точность. Этот параметр присутствует в технических характеристиках многих приборов, которые имеют эталонные выходные параметры, будь то электронные или механические измерительные устройства. Класс точности является основной характеристикой измерительной техники: весов, мультиметров, осциллографов, КИПовского оборудования и прочего. Чем выше это значение у прибора, тем больше стоит такое устройство, это связано со сложностью производства таких изделий.

Нормированная погрешность

Класс точности приборов измерений характеризует свойства таких изделий по отношению к точности, но при этом не является показателем точности этих измерений, выполненных при помощи данного устройства. С целью преждевременного выявления погрешности прибора, которую данное средство внесет в измеряемый результат, используют нормированные значения погрешностей. Значение этого параметра у каждого технического приспособления одной группы является индивидуальным, оно имеет отличные друг от друга случайные и систематические составляющие, но такая погрешность любого измерительного прибора одного класса не должна превышать установленное нормированное значение. Границы главной погрешности и коэффициента влияния заносятся в паспорт любого измерительного прибора. Все основные методы нормирования допустимых погрешностей и обозначения класса измеряющих устройств установлены ГОСТом, например, класс точности весов предусмотрен ГОСТом 24104-2001, который вступил в силу 01.07.2002.

Виды маркирования

Класс точности любого измерительного прибора маркируется на шкале устройства в виде числа. Это значение указывает нормированную величину погрешности, выраженную в процентном отношении. Если класс точности на шкале прибора обведен кружком, например 2,5, то это значит, что величина погрешности чувствительности устройства составляет 2,5 процента. По такому принципу нормируют погрешность масштабных преобразователей (измерительных шунтов, делителей напряжения, измерителей трансформаторов напряжения и тока и т. п.). Если значение класса точности на шкале прибора не подчеркнуто, например 0,7, это значит, что устройство нормируется погрешностью нуля равным 0,7. Эти приборы при любых з

Способы нормирования допускаемых погрешностей:
— по абсолютной погрешности,
— по относительной погрешности,
— по приведенной погрешности – по длине или верхнему пределу шкалы прибора.

Обозначения классов точности измерительных приборов:

— арабскими цифрами без условных знаков — класс точности определяется пределами приведённой погрешности, в качестве нормирующего значения используется наибольший по модулю из пределов измерений.

— арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы.

По приведенной погрешности приборы делятся на классы (8 классов стрелочных приборов): 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Приборы класса точности 0,05; 0,1; 0,2; 0,5 применяются для точных лабораторных измерений и называются прецизионными.

В технике применяются приборы классов 1,0; 1,5: 2,5 и 4,0 (технические).

Если на шкале такого обозначения нет, то данный прибор внеклассный, то есть его приведенная погрешность превышает 4%.

— арабскими цифрами в кружке — класс точности определяется пределами относительной погрешности.

— латинскими буквами, то класс точности определяется пределами абсолютной погрешности.

Когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены наименьшего деления. При считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.

КАК ВЫЧИСЛИТЬ ПОГРЕШНОСТЬ

Класс точности определяется как отношение той или иной погрешности к точному значению.
Абсолютную можно представить в виде разности между точным и приблизительным значениями х и а, в виде формулы s=(x-a)
Относительная определяется как отношение этой же разнице к величине а,
а приведенная – к длине шкалы l. Умножьте полученный результат на 100%.

Большая Энциклопедия Нефти и Газа

Класс — точность — измерительный прибор

Класс точности измерительного прибора — обобщенная характеристика прибора, определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами прибора, влияющими на точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений. Класс точности характеризует свойства приборов в отношении точности, но не является непосредственным показателем точности измерений, выполняемых с помощью этих приборов. Например, класс точности вольтметров характеризует пределы допускаемой основной погрешности и допускаемых изменений показаний, вызываемых внешним магнитным полем и отклонениями от нормальных значений температуры, частоты переменного тока и некоторых других влияющих величин. [1]

Класс точности измерительного прибора — это число, которое соответствует наибольшей погрешности, допустимой нормами. Класс точности выражается в процентах от верхнего предела измерения прибора. Например, термометр класса 1 может иметь допустимую погрешность 1 % от верхнего предела шкалы. [2]

Класс точности измерительного прибора определяется наибольшей допустимой погрешностью в процентах величины, соответствующей предельному значению шкалы прибора. [3]

Класс точности измерительных приборов нормируется как обобщенная характеристика средств измерений, определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на их точность, значения которых устанавливаются стандартами на соответствующие виды измерительных приборов. [4]

Классом точности измерительного прибора называется его характеристика, которая определяет степень точности измерения, пределы основной погрешности. Для приборов теплотехнического контроля холодильных установок класс точности численно равен максимальной величине приведенной основной погрешности, выраженной в процентах. [5]

Что характеризует класс точности измерительных приборов . [6]

Приведенная допустимая погрешность определяет класс точности измерительного прибора . [7]

Значение какой величины определяет обозначение класса точности измерительного прибора . [8]

Предельные значения основной и дополнительной погрешностей определяют класс точности измерительного прибора , который задается двумя способами: по величине абсолютной погрешности и по величине наибольшей допустимой основной приведенной погрешности в виде абсолютного числа, совпадающего с пределом допустимой погрешности для конечного значения рабочей части шкалы. [9]

В физико-химических иследованиях первый путь равносилен увеличению класса точности измерительных приборов или переходу к более прецизионным методам измерений. Второй путь представляется более доступным, но он пригоден лишь применительно к измерению экстенсивных величин. Кроме того, для успешного использования этого приема нужно быть уверенным в том, что абсолютная погрешность измерений не коррелирует с массой исследуемого образца и, следовательно, с измеряемым экстенсивным свойством. Так, если абсолютная погрешность измерения энтальпии сгорания для калориметра данной конструкции есть величина приблизительно постоянная для заданного интервала значений 100 — 5000 Дж, с целью снижения относительной погрешности определения следует сжигать навески, обеспечивающие большое тепловыделение. [10]

Максимальная погрешность этих измерений известна и определяется классом точности примененных измерительных приборов . [11]

При различных экспериментальных работах очень важно правильно выбрать класс точности используемых измерительных приборов . Под точностью прибора понимают его свойство, характеризующее степень приближения показаний данного прибора к действительным значениям измеряемой величины. Обычно точность прибора задается классом точности прибора или указывается в его паспорте. Очевидно, что чем точнее прибор, тем меньше его погрешность и выше стоимость. [12]

Допустимое отношение сигнал / помеха зависит также от класса точности измерительного прибора . [13]

А ( / — ошибка измерения, которая определяется классом точности измерительного прибора ; ДХ — допустимая погрешность измерения моделируемой величины. [14]

Особо специфическими являются требования, предъявляемые некоторыми стандартами в отношении класса точности измерительных приборов , применяемых при испытаниях. [15]

Погрешности средств измерений. Класс точности прибора

В результате воздействия большого числа факторов, влия­ющих на изготовление и эксплуатацию средств измерений, по­казания приборов отличаются от истинных значений измеряе­мых ими величин. Эти отклонения характеризуют погрешность средств измерений. Погрешности СИ в отличие от погрешности измерений имеют другую физическую природу, так как они от носятся к СИ, с помощью которого осуществляют измерение. Они являются лишь составной частью погрешности измерения.

Классификация погрешностей средств измерений в зависи­мости от разных признаков:

В понятия абсолютной, относительной, систематической и случайной погрешностей вкладывается тот же смысл, что и в понятия погрешностей измерений.

Приведенная погрешность средства измерений равна отноше­нию абсолютной погрешности прибора ΔХ к некоторому норми­рующему значению X_N :

Таким образом, приведенная погрешность является разновид­ностью относительной погрешности прибора. В качестве норми­рующего значения X_N принимают диапазон измерений, верх­ний предел измерений, длину шкалы и др.

Основная погрешность — погрешность средства измерений, используемого в нормальных условиях. При эксплуатации СИ на производстве возникают значительные отклонения от нор­мальных условий, вызывающие дополнительные погрешности.

Нормальными условиями для линейных измерений считают­ся:

• температура окружающей среды 20°С

• атмосферное давление 101325 Па (760 мм рт.ст.)

• относительная влажность окружающего воздуха 58%

• ускорение свободного падения 9,8 м/с

• направление линии и плоскости измерения — горизонтальное

• относительная скорость движения внешней воздушной среды равна нулю.

В тех случаях, когда средство измерения применяется для измерения постоянной или переменной во времени величины, для его характеристики используют понятия статическая и динамическая погрешности соответственно. Динамическая погрешность определяется как разность между погрешностью измерения в динамическом режиме и его статической погрешностью, равной значению величины в данный момент времени. Динами­ческие погрешности возникают вследствие инерционных свойств средств измерения.

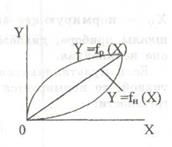
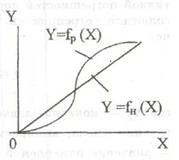
Для рассмотрения зависимости погрешности средства измерения от значения измеряемой величины используют понятие номинальной и реальной функций преобразования — соответствен­но Y = fн(Х) и Y = fр(X).

Номинальная функция преобразования приписана измери­тельному устройству, указывается в его паспорте и используется при выполнении измерений.

Реальной функцией преобразования называют ту, которой обладает конкретный экземпляр СИ дан­ного типа.

Реальная функция преобразования имеет отклонение от но­минальной функции и связана со значением измеряемой вели­чины. Систематическую погрешность в функции измеряемой величины можно представить в виде суммы погрешности схемы, определяемо самой структурной схемой средства измерений, и технологических погрешностей, обусловленных погрешностями изготовления его элементов. Технологические погрешности принято разделять на аддитивную, мультипликативную, гистерезиса и линейности.

Аддитивной погрешностью (получаемой путем сложения), или погрешностью нуля, называют погрешность, которая оста­ется постоянной при всех значениях измеряемой величины.

Мультипликативная погрешность (получаемая путем умно­жения), или погрешность чувствительности СИ, линейно воз­растает или убывает с изменением измеряемой величины. В большинстве случаев аддитивная и мульти­пликативная составляющие присутствуют одновременно.

Погрешность гистерезиса, или Погрешность обратного хода, выражается в несовпадении реальной функции преобразования при увели­чении (прямой ход) и уменьшении (обратный ход) измеряемой величины. Если взаимное распо­ложение номинальной и реальной функций преобразования средства измерений вызвано нелинейностью, то эту погрешность называют погрешностью линейности.

В разных точках диапазона средств измерений погрешность может принимать различные значе­ния. В этом случае необходимо нор­мировать пределы допускаемых по­грешностей, т.е. устанавливать грани­цы, за пределы которых погрешность не должна выходить ни при изготовлении, ни в процессе эксплуатации. Для этого служит класс точности СИ.

Класс точности — это обобщенная характеристика, определяемая пре­делами допускаемых основных и до­полнительных погрешностей, а также другими свойствами, влия­ющими на точность, значения кото­рых устанавливают в стандартах на отдельные виды средств измерений.

Способы установления классов точности изложены в ГОСТ 8.401 “ГСИ. Классы точности средств измерения. Общие требования”. Стандарт не распространяется на средства измерений, для которых предусматриваются раздельные нормы на систематическую и случайные составляющие, а также на средства измерений, для которых нормированы номинальные функции влияния, а измерения проводятся без введения поправок на влияющие величины. Классы точности не устанавливаются и на средства измерений, для которых существенное значение имеет динамическая погрешность.

Класс точности не является непо­средственным показателем точности измерений, так как точность изме­рений зависит еще от метода и ус­ловий измерений.

В зависимости от вида погреш­ности средства измерений существу­ет несколько способов нормирования погрешности.

Если аддитивная погрешность СИ преобладает над мультипликативной, удобнее нормировать абсолютную или приведенную погрешности соответственно:

Нормирование по абсолютной погрешности не позволяет срав­нивать по точности приборы с разными диапазонами измерений, поэтому принято нормировать приведенную погрешность, где р — отвлеченное положительное число, выбираемое из ряда

(1,5; 2; 2,5; 4; 5; 6) 10* (п = 1, О, — 1, — 2 и т.д.);

X_N — нормирующее значение, равное конечному значению шкалы прибора, диапазону измерений или длине шкалы, если она нелинейная.

Если мультипликативная погрешность преобладает над адди­тивной, то нормируется предел допускаемой относительной по­грешности:

где q — отвлеченное положительное число, выбираемое из ряда, приведенного для р.

При одновременном проявлении аддитивной и мультиплика­тивной погрешностей нормируется предел относительной или аб­солютной погрешностей, определяемых формулами соответствен­но:

,

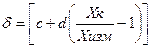где Хк — конечное значение шкалы прибора; с и d — положи­тельные числа, выбираемые из ряда, приведенного для р; Xизм — значение измеряемой величины на входе(выходе) средств измерений или число делений, отсчитанных по шкале; а и b положительные числа, не зависящие от Xизм.

Обозначение классов точности в документации и на средствах измерений приведены в табл.

Если пределы допускаемой погрешности средств измерений задаются в виде графиков, таблиц или в сложной форме, то классы точности обозначаются римскими цифрами или прописными буквами латинского алфавита.

Регулировка и градуировка средств измерений

В большинстве случаев в измерительном приборе (преобразователе) можно найти или предусмотреть такие элементы, вариация параметров которых наиболее заметно сказывается на его систематической погрешности, главным образом погрешности схемы, аддитивной и мультипликативной погрешностях.

В общем случае в конструкции измерительного прибора должны быть предусмотрены два регулировочных узла: регулировка нуля и регулировка чувствительности. Регулировкой нуля уменьшают влияние аддитивной погрешности, постоянной для каждой точки шкалы, а регулировкой чувствительности уменьшают мультипликативные погрешности, меняющиеся линейно с изменением измеряемой величины. При правильной регулировке нуля и чувствительности уменьшается и влияние погрешности схемы прибора. Кроме того, некоторые приборы снабжаются устройствами для регулировки погрешности схемы (пружинные манометры).

Таким образом, под регулировкой средств измерения понимается совокупность операций, имеющих целью уменьшить основную погрешность до значений, соответствующих пределам ее допускаемых значений, путем компенсации систематической составляющей погрешности средств измерений, т.е. погрешности схемы, мультипликативной и аддитивной погрешностей.

Градуировкой называется процесс нанесения отметок на шкалы средств измерений, а также определение значений измеряемой величины, соответствующих уже нанесенным отметкам, для составления градуировочных кривых или таблиц.

Различают следующие способы градуировки:

— использование типовых (печатных) шкал, которые изготовляются заранее в соответствии с уравнением статической характеристики идеального прибора;

— индивидуальная градуировка шкал. Индивидуальную градуировку шкал осуществляют в тех случаях, когда статическая характеристика прибора нелинейна или близка к линейной, но характер изменения систематической погрешности в диапазоне измерения случайным образом меняется от прибора к прибору данного типа так, что регулировка не позволяет уменьшить основную погрешность до пределов ее допускаемых значений. Индивидуальную градуировку проводят в следующем порядке. На предварительно отрегулированном приборе устанавливают циферблат с еще не нанесенными отметками. К измерительному прибору подводят последовательно измеряемые величины нескольких наперед заданных или выбранных значений. На циферблате нанося отметки, соответствующие положениям указателя при этих значениях измеряемо величины, а расстояния между отметками делят на равные части. При индивидуальной градуировке систематическая погрешность уменьшается во всем диапазоне измерения, а в точках, полученных при градуировке, она достигает значения, равного погрешности обратного хода;

— градуировка условной шкалы. Условной называется шкала, снабженная некоторыми условными равномерно нанесенными делениями, например, через миллиметр или угловой градус. Градуировка шкалы состоит в определении при помощи образцовых мер или измерительных приборов значений измеряемой величины соответствующих некоторым отметкам, нанесенным на ней. В результате определяют зависимость числа делений шкалы, пройденных указателем, от значений измеряемой величины. Эту зависимость представляют в виде таблицы или графика. Если необходимо избавиться и от погрешности обратного хода. Градуировку осуществляют раздельно при прямом и обратном ходе.