Все углы правильного шестиугольника равны 135

Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.

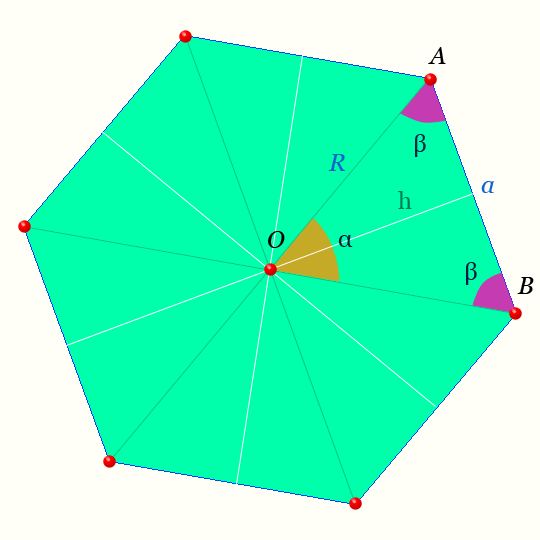
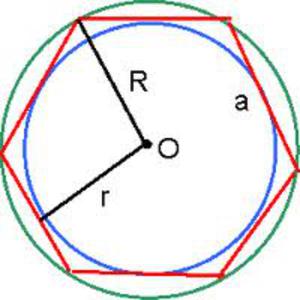
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA , OB — радиусы правильного шестиугольника.

Обозначения на рисунке для правильного шестиугольника

Основные формулы для правильного шестиугольника

Периметр правильного шестиугольника

Полупериметр правильного шестиугольника

Центральный угол правильного шестиугольника в радианах

Центральный угол правильного шестиугольника в градусах

Половина внутреннего угла правильного шестиугольника в радианах

Половина внутреннего угла правильного шестиугольника в градусах

Внутренний угол правильного шестиугольника в радианах

Внутренний угол правильного шестиугольника в градусах

Площадь правильного шестиугольника

Отсюда получим апофему правильного шестиугольника

Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

чертится прямая линия и на ней ставится точка;
из этой точки строится окружность (она является ее центром);
из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
после этого отрезками последовательно соединяются все точки на первой окружности.

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Свойства простые и интересные

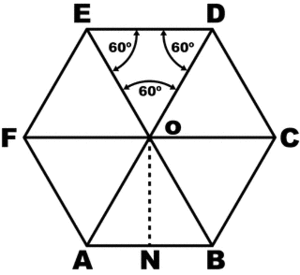
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

диаметр описанной окружности;
диаметр вписанной окружности;
площадь;
периметр.

Описанная окружность и возможность построения

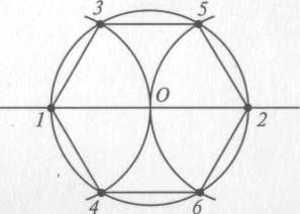Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

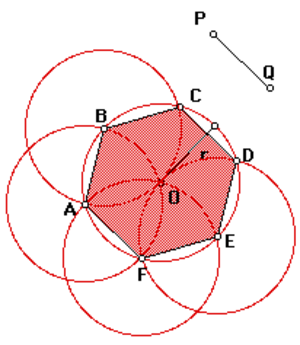Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

r₂=а/2

Площадь нового шестиугольника можно посчитать так:

Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.

Правильный многоугольник

Правильный многоугольник — это многоугольник, все стороны и углы которого равны.

Вокруг правильного многоугольника можно описать окружность и в него можно вписать окружность. Центры этих окружностей совпадают.

Правильный шестиугольник

Правильный шестиугольник – это шестиугольник, все стороны и углы которого равны.

Описанный многоугольник

Если все стороны многоугольника касаются некоторой окружности , то он называется описанным многоугольником .

Scisne ?

Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.

Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку

Все углы равны 120°.

Радиус вписанной окружности равен:

Периметр правильного шестиугольника равен:

Площадь правильного шестиугольника рассчитывается по формулам:

Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.

Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.

Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — <6,3>, что означает, что в каждой вершине паркета сходятся три шестиугольника.

Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.

Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.

Пчелиные соты показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.

Читать еще: Как правильно заточить охотничий нож

Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.

Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.

Гигантский гексагон — атмосферное явление на Сатурне.

Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.

Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.

Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.

Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.

Игровое поле зачастую составляют шестиугольники. Замощение плоскости правильными шестиугольниками является основой для гекса, гексагональных шахмат и других игр на клетчатом поле, полигексов, вариантов модели «Жизнь» и других двумерных клеточных автоматов, кольцевых флексагонов и т.п.

Сечение гайки имеет вид правильного шестиугольника.

Звезда Давида (гексаграмма) — шестиконечная звезда, образованная двумя правильными треугольниками, символ иудаизма.

Правильный шестиугольник

Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.

Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.

Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?

Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.

Мы знаем, что площадь правильного треугольника: .

Тогда площадь правильного шестиугольника — в шесть раз больше.

, где — сторона правильного шестиугольника.

Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.

Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.

Ты нашел то, что искал? Поделись с друзьями!

. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Радиус такой окружности равен .

. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Обучающее видео
БЕСПЛАТНО

Техническая поддержка:
help@ege-study.ru (круглосуточно)

Пробные репетиционные ЕГЭ: пройдите бесплатное тестирование! Все, как на настоящем ЕГЭ.
Звоните, чтобы записаться:

8 (495) 984-09-27 или 8 (800) 775-06-82

Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.

Все поля обязательны для заполнения

Премиум

Вся часть 2 на ЕГЭ по математике, от задачи 13 до задачи 19. То, о чем не рассказывают даже ваши репетиторы. Все приемы решения задач части 2. Оформление задач на экзамене. Десятки реальных задач ЕГЭ, от простых до самых сложных.

Видеокурс «Премиум» состоит из 7 курсов для освоения части 2 ЕГЭ по математике (задачи 13-19). Длительность каждого курса — от 3,5 до 4,5 часов.

Уравнения (задача 13)
Стереометрия (задача 14)
Неравенства (задача 15)
Геометрия (задача 16)
Финансовая математика (задача 17)
Параметры (задача 18)
Нестандартная задача на числа и их свойства (задача 19).

Здесь то, чего нет в учебниках. Чего вам не расскажут в школе. Приемы, методы и секреты решения задач части 2.

Каждая тема разобрана с нуля. Десятки специально подобранных задач, каждая из которых помогает понять «подводные камни» и хитрости решения. Автор видеокурса Премиум — репетитор-профессионал Анна Малкова.

Получи пятерку

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.

Задачи комплекта «Математические тренинги — 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.

Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.

Как пользоваться?

Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по однойи старайтесь довести до ответа.
Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Вам помогут книга для подготовки к ЕГЭи Годовой Онлайн-курс.
Если вы правильно решили из первого варианта Маттренингов 5-7 задач – значит, знаний не хватает. Смотри пункт 1: Книгаи Годовой Онлайн-курс!
Обязательно разберите правильные решения. Посмотрите видеоразбор – в нем тоже много полезного.
Можно решать самостоятельно или вместе с друзьями. Или всем классом. А потом смотреть видеоразбор варианта.

Стоимость комплекта «Математические тренинги – 2019» — всего 1100 рублей. За 5 вариантов с решениями и видеоразбором каждого.

Информационные технологии на уроках математики. Правильные многоугольники

Оборудование:

Медиапроектор. Экран.
Презентация “Правильные многоугольники”
Модели правильных и неправильных многоугольников.

Цели:

Повторить формулу суммы углов выпуклого многоугольника.
Ввести понятие правильного многоугольника.
Вывести формулу для вычисления угла правильного многоугольника и показать её применение в ходе решения задач.
Развивать вычислительные навыки, логическое мышление учащихся, прививать им навыки самостоятельности, умение работать в группе.

Этапы урока.

I. Организационный момент.

Сообщить учащимся тему и цели урока.

II. Актуализация знаний учащихся.

С целью подготовки учащихся к восприятию нового материала решить задачи на повторение темы сумма углов выпуклого многоугольника.

Найдите сумму углов выпуклого восьмиугольника.

(n – 2) · 180 о — сумма углов выпуклого n-угольника.

Т. к. n = 8, то (8 – 2) · 180 о = 6 · 180 о = 1080 о

Все углы выпуклого шестиугольника равны. Найдите величину одного из них.

Сумма углов шестиугольника:

(6 – 2) · 180 о = 4 · 180 о = 720 о

Т. к. все углы равны, то каждый равен: 720 о : 6 = 120 о

III. Изучение нового материала.

1. Ввести понятие правильного многоугольника.

Выпуклый многоугольник называется правильным, если все его углы и все его стороны равны.

2. Устные упражнение на закрепление понятия правильного многоугольника.

Какой треугольник называется правильным? Почему?

[Равносторонний, т. к. все его стороны и все углы равны.]

Является ли правильным четырёхугольником:

— прямоугольник? [Нет. Его стороны не всегда равны]

Читать еще: Редуктор от сгоревшей болгарки

— ромб? [Нет. Его углы не всегда равны]

— квадрат? [Да. Все его стороны и все углы равны]

3. Работа в творческих группах.

Учащиеся группами по 2-4 человека в каждой решают задачу.

Чему равен каждый из углов правильного:

Обсуждение решения задачи.

Т. к. все 10 углов равны, то каждый из них равен 1440 о :10 = 144 о

б) (n – 2) · 180 о — сумма всех углов n-угольника.

Т. к. все n углов равны, то каждый из них равен: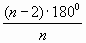

Вывод: формула для вычисления градусной меры a угла правильного n – угольника имеет вид: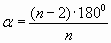

Решение задач № 1081 (б, д) и 1083 (а, в) с помощью учителя в творческих группах с последующим обсуждением.

Дано: a – угол правильного n – угольника

Найти: a

б)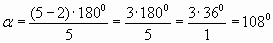

д)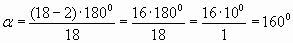

Дано: а – угол правильного n – угольника

1) решим, сначала, задачу в общем виде

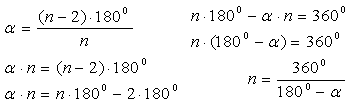
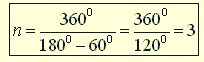
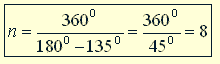
Ответ: а) три; б) восемь

Итог урока. Подвести итоги урока.

VI. Домашнее задание: п. 105, вопросы 1-2, № 1081 (в, г), 1083 (б, г).

Дополнительная задача (для учащихся, увлечённых математикой)

Докажите, что в правильном пятиугольнике, диагонали, выходящие из одной вершины делят угол при этой вершине на три равных угла.

ЕГЭ по математике (2019 год). Задания №1 с ответами, профильные — часть 65

Дан правильный многоугольник, вписанный в окружность. Угол между двумя соседними сторонами многоугольника равен 156°. Рассчитайте число вершин многоугольника

Каждый угол правильного многоугольника равен 180° * (n – 2) / n , где n – число его углов (вершин)

Составляем уравнение: 180 * ( n – 2 ) / n=156

180*n – 360 = 156 * n

В четырехугольник ABCD вписана окружность, AB= 35, BC=10, CD=71. Найдите четвертую сторону четырехугольника

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD

Дан треугольник АВС. Его площадь равна 133. DE – средняя линия, параллельная стороне AB. Рассчитайте площадь трапеции ABED

Площадь трапеции ABED можно найти как разность площадей двух треугольников:

Площадь треугольника CED будет в 4 раза меньше площади треугольника ABC, так как линейные размеры треугольника CED в 2 раза меньше соответствующих размеров треугольника ABC

По найденной формуле вычисляем, что площадь трапеции ABED=99,75

У прямоугольной трапеции, описанной около окружности, периметр равен 52, большая боковая сторона равна 20 . Найдите радиус окружности

Сторона AD равна диаметру окружности, значит R=AD/2

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD

У трапеции, описанной около окружности, боковые стороны равны 43 и 55 . Найдите среднюю линию трапеции

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD

Средняя линия MK = (DC+AB) / 2 = (AD+BC) / 2 = 98 / 2 = 49

Дана равнобедренненная трапеция. Её основания равны 12 и 6. Синус острого угла трапеции равен 0,8. Рассчитайте боковую сторону

Треугольники ADH и BKC равны (так как AD=CD и DH=CK), значит, AH=KB

Треугольник ADH прямой, поэтому гипотенуза AD = AH / cos(a)

По найденной формуле вычисляем, что AD=5

Дан треугольник ABC. Стороны AC=27, BC=120, угол C равен 90° . Рассчитайте радиус окружности, вписанной в этот треугольник

Радиус вписанной в прямоугольный треугольник окружности равен половине разности суммы катетов и гипотенузы:

Подставим в формулу вместо значение AC и BC и решим уравнение

Площадь параллелограмма ABCD равна 133. Точка E – середина стороны CD. Рассчитайте площадь треугольника ADE

Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 4,

треугольник ADE, состоит из одного такого треугольника, значит его площадь равна 1/4 от площади параллеаграмма ABCD

По найденной формуле вычисляем, что площадь треугольника ADE=33,25

Окружность вписана в четырёхугольник ABCD, периметр = 132, стророна AB= 31 . Найдите длину стороны CD

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD

Значит P / 2 = AB + CD

В равнобедренном треугольнике боковые стороны равны 60, основание равно 72 . Рассчитайте радиус окружности, вписанной в этот треугольник

Радиус вписанной окружности равен отношению площади к полупериметру. Для нахождения площади, воспользуемся формулой Герона:

Подставим значения сторон треугольника и найдём площадь. Она равна S=1728

Подствавим значения и найдём полупериметр P=96

Подствавим значения и найдём радиус r=1728/96=18

Основания равнобедренной трапеции равны 40 и 14. Радиус описанной окружности равен 25. Центр окружности лежит внутри трапеции. Найдите высоту трапеции

Построим высоту KH через центр окружности O

Из рисунка видно, что треугольники DOC и AOB – равнобедренные и их высоты KO и HO делят стороны DC и AB пополам. Найдем эти высоты из прямоугольных треугольников DKO и AOH по теореме Пифагора, имеем:

Подставим известные значения в формулы и вычислим KO и HO

Следовательно, высота трапеции равна KH=KO+HO=24+15=39

Примечание: Если бы большее основание трапеции лежало выше центра окружности (то есть оба основания располагались по одну сторону от центра окружности) длина высоты равнялась бы не сумме, а разности найденных отрезков. Решая данную задачу необходимо принимать во внимание рисунок, данный в условии

У трапеции, описанной около окружности, периметр равен 97. Рассчитайте длину средней линии трапеции

Периметр — сумма всех сторон трапеции

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD

Средняя линия MK = 97 / 4 = 24,25

Периметр (Р) правильного шестиугольника равен 414. Найдите диаметр описанной окружности

Периметр (P) — сумма длин всех сторон, поэтому:

AB / 6 = P / 6 =414 / 6 = 69

Рассмотрим угол AOB. Он равен 60°, т.к. вся окружность 360°, а треугольников 6 (360°/6=60°)

Рассмотрим треугольник AOB. Он равносторонний, т.к. AO=OB=R и угол AOB=60° и тогда

Дан равнобедренный треугольник. Окружность, вписанная в треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 49 и 15, считая от вершины, противолежащей основанию. Вычислите периметр треугольника

Пусть точки H и K являются точками касания окружности и сторон AB и СВ соответственно.

Треугольники KOH и KOB равны, т.к. являются прямоугольными с общей гипотенузой и равными катетами, значит, HB=KB=15

Периметр треугольника равен P=AC+CB+AH+HB=2CB+2HB=128+30=158

Дан параллелограмм ABCD. Его площадь равна 132. Середины его сторон являются вершинами параллелаграмма A′B′C′D′. Найдите площадь параллелограмма A′B′C′D′

Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 8,

параллелограмм A′B′C′D′ состоит из четырёх таких треугольников, значит, его площадь равна 1/2 от площади параллеаграмма ABCD

По найденной формуле вычисляем, что площадь параллелограмма A′B′C′D′=66

Дана окружность, вписанная в треугольник ABC, к которой проведены три касательные. Периметры отсеченных треугольников равны 19, 48, 68. Рассчитайте периметр данного треугольника

EF и ED — отрезки касательных, проведенных из одной точки Е. Они по свойству касательных равны. Аналогично, GF = GH. То есть, GE = GH + ED, а периметр треугольника AGE запишется как

Площадь параллелограмма ABCD равна 135. Середина стороны BC — точка E. Вычислите площадь трапеции ADEB

Разобьём параллеаграмм ABCD на равные треугольники (как на рисунке) — всего их 4,

трапеция ADEB, состоит из трёх таких треугольников, значит площадь трапеции ADEB равна 3/4 от площади параллеаграмма ABCD

По найденной формуле вычисляем, что площадь трапеции ADEB=101,25

Катеты равнобедренного прямоугольного треугольника равны 94+47√2 . Найдите радиус окружности, вписанной в этот треугольник

Пусть катеты прямоугольного треугольника равны a, тогда гипотенуза AB, равна:

Подставим в формулу вместо а значение катетов и решим уравнение

В четырёхугольник ABCD вписана окружность, сторона AB= 51, CD= 36 . Рассчитайте периметр четырёхугольника ABCD

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD

Периметр (P) четырехугольника – это сумма длин всех его сторон, то есть P=AB+BC+AD+CD= 2*(AB+CD)

Даны два угла вписанного в окружность четырехугольника. Они равны 48° и 90°. Рассчитайте больший из оставшихся углов. Ответ дайте в градусах.

Cумма противоположных углов в четырехугольнике, вписанном в окружность равна 180 градусов (теорема Птолемея)

угол противоположный углу 48 градусов равен 180-48=132 градусов

угол противоположный углу 90 градусов равен 180-90=90 градусов

§ 1. Правильные многоугольники

Правильный многоугольник

Вы знаете, как измеряются отрезки и как измеряются площади многоугольников. Вам известны формулы, по которым можно вычислить площади треугольника и некоторых четырёхугольников. А как вычислить длину окружности и площадь круга, если известен их радиус? Ответ на этот вопрос вы найдёте в этой главе. Но сначала нам предстоит познакомиться с красивыми геометрическими фигурами — правильными многоугольниками, вывести для них важные формулы, а затем уже с их помощью мы получим формулы длины окружности и площади круга.

Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

Примерами правильных многоугольников являются равносторонний треугольник и квадрат. На рисунке 306 изображены правильные пятиугольник, семиугольник и восьмиугольник.

Выведем формулу для вычисления угла α_n правильного n-угольника. Сумма всех углов такого n-угольника равна (n — 2) • 180°, причём все его углы равны, поэтому

Окружность, описанная около правильного многоугольника

Напомним, что окружность называется описанной около многоугольника, если все вершины многоугольника лежат на этой окружности. Докажем теорему об окружности, описанной около правильного многоугольника.

Пусть А₁А₂А₃. А_n — правильный многоугольник, О — точка пересечения биссектрис углов А₁ и А₂ (рис. 307).

Соединим точку О отрезками с остальными вершинами многоугольника и докажем, что ОА₁ = ОА₂ = . = ОА_n. Так как ∠A₁ = ∠A₂, то ∠1 = ∠3, поэтому треугольник А₁А₂O равнобедренный: в нём ОА₁ = ОА₂. Треугольники А₁A₂О и А₂А₃О равны по двум сторонам и углу между ними (A₁A₂ = А₃А₂, А₂O — общая сторона и ∠3 = ∠4), следовательно, ОА₃ = ОА₁. Точно так же можно доказать, что ОА₄ = ОА₂, ОА₅ = ОА₃ и т. д.

Читать еще: Ремонт светодиодных ламп автомобиля

Итак, ОА₁ = ОА₂ = . = ОА n, т. е. точка О равноудалена от всех вершин многоугольника. Поэтому окружность с центром О и радиусом OA₁ является описанной около многоугольника.

Докажем теперь, что описанная окружность только одна. Рассмотрим какие-нибудь три вершины многоугольника, например А₁, А₂, А₃. Так как через эти точки проходит только одна окружность, то около многоугольника A₁A₂A₃. A_n можно описать только одну окружность. Теорема доказана.

Окружность, вписанная в правильный многоугольник

Напомним, что окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. Докажем теорему об окружности, вписанной в правильный многоугольник.

Пусть А 1А₂. А_n — правильный многоугольник, О — центр описанной окружности (рис. 308). В ходе доказательства предыдущей теоремы мы установили, что ΔОА₁А₂ = ΔОА₂А₃ = . = ΔОА_nА₁, поэтому высоты этих треугольников, проведённые из вершины О, также будут равны: ОН₁ = ОН₂ =. = ОН_n. Отсюда следует, что окружность с центром О и радиусом ОН₁ проходит через точки H₁, Н₂, . Н_n и касается сторон многоугольника в этих точках, т. е. эта окружность вписана в данный правильный многоугольник.

Докажем теперь, что вписанная окружность только одна.

Предположим, что наряду с окружностью с центром О и радиусом ОН₁ есть и другая окружность, вписанная в многоугольник А₁А₂. А_n. Тогда её центр О₁ равноудалён от сторон многоугольника, т. е. точка О₁ лежит на каждой из биссектрис углов многоугольника и, следовательно, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. равен ОН₁. Таким образом, вторая окружность совпадает с первой. Теорема доказана.

Эта точка называется центром правильного многоугольника.

Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности

Пусть S — площадь правильного n-угольника, а_n — его сторона, Р — периметр, а r и R — радиусы соответственно вписанной и описанной окружностей. Докажем сначала, что

Соединим центр данного многоугольника с его вершинами (см. рис. 308). Тогда многоугольник разобьётся на n равных треугольников, площадь каждого из которых будет равна Следовательно,

Выведем далее формулы:

Для вывода этих формул воспользуемся рисунком 308. В прямоугольном треугольнике А₁Н₁О

Полагая в формуле (2) n = 3, 4 и 6, получим выражения для сторон правильного треугольника, квадрата и правильного шестиугольника:

Построение правильных многоугольников

Рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Построения правильного треугольника и правильного четырёхугольника, т. е. квадрата, рассматривались ранее. Для построения правильных п-угольников при n > 4 обычно используется окружность, описанная около многоугольника.

Построить правильный шестиугольник, сторона которого равна данному отрезку.

Для решения задачи воспользуемся формулой (4). Пусть PQ — данный отрезок. Построим окружность радиуса PQ и отметим на ней произвольную точку А₁ (рис. 309). Затем, не меняя раствора циркуля, построим на этой окружности точки А₂, А₃, А₄, А₅, А₆ так, чтобы выполнялись равенства А₁А₂ = А₂А₃ = А₃А₄ = А₄А₅ = А₅А₆. Соединяя последовательно построенные точки отрезками, получим искомый правильный шестиугольник А₁А₂А₃А₄А₅А₆.

Для построения правильных многоугольников часто используется следующая задача:

Дан правильный n-угольник. Построить правильный 2n-угольник.

Пусть A₁A₂. A_n — данный правильный n-угольник. Опишем около него окружность. Для этого построим биссектрисы углов А₁ и А₂ и обозначим буквой О точку их пересечения. Затем проведём окружность с центром О радиуса ОА₁ (см. рис. 307).

Для решения задачи достаточно разделить дуги А₁А₂, А₂А₃, . A_nA₁ пополам и каждую из точек деления В₁, В₂, . В_n соединить отрезками с концами соответствующей дуги (рис. 310, на этом рисунке n = 6). Для построения точек В₁, В₂, . В_n можно воспользоваться серединными перпендикулярами к сторонам данного n-угольника. На рисунке 310 таким способом построен правильный двенадцатиугольник A₁B₂А₂B₂. A₆B₆.

Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный четырёхугольник, т. е. квадрат, и пользуясь результатом задачи 2, можно построить правильный восьмиугольник, затем правильный шестнадцатиугольник и вообще правильный 2 k -угольник, где k — любое целое число, большее двух.

Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Оказывается, однако, что не все правильные многоугольники допускают такое построение. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки. Любопытно, что с помощью этих инструментов можно построить правильный семнадцатиугольник.

Задачи

1078. Верно ли утверждение: а) любой правильный многоугольник является выпуклым; б) любой выпуклый многоугольник является правильным? Ответ обоснуйте.

1079. Какие из следующих утверждений верны: а) многоугольник является правильным, если он выпуклый и все его стороны равны; б) треугольник является правильным, если все его углы равны; в) любой равносторонний треугольник является правильным; г) любой четырёхугольник с равными сторонами является правильным? Ответ обоснуйте.

1080. Докажите, что любой правильный четырёхугольник является квадратом.

1081. Найдите углы правильного n-угольника, если: а) n = 3; б) n = 5; в) n = 6; г) n = 10; д) n = 18.

1082 Чему равна сумма внешних углов правильного n-угольника, если при каждой вершине взято по одному внешнему углу?

1083. Сколько сторон имеет правильный многоугольник, если каждый его угол равен: а) 60°; б) 90°; в) 135°; г) 150°?

1084. Сколько сторон имеет правильный вписанный многоугольник, если дуга описанной окружности, которую стягивает его сторона, равна: а) 60°; б) 30°; в) 90°; г) 36°; д) 18°; е) 72°?

1085. Докажите, что серединные перпендикуляры к любым двум сторонам правильного многоугольника либо пересекаются, либо совпадают.

1086. Докажите, что прямые, содержащие биссектрисы любых двух углов правильного многоугольника, либо пересекаются, либо совпадают.

1087. На рисунке 311, а изображён квадрат, вписанный в окружность радиуса R. Перечертите таблицу в тетрадь и заполните пустые клетки (а4 — сторона квадрата, Р — периметр квадрата, S — его площадь, г — радиус вписанной окружности).

1088. На рисунке 311,6 изображён правильный треугольник, вписанный в окружность радиуса R. Перечертите таблицу в тетрадь и заполните пустые клетки (а₃ — сторона треугольника, Р — периметр треугольника, S — его площадь, r — радиус вписанной окружности).

1089. Периметр правильного треугольника, вписанного в окружность, равен 18 см. Найдите сторону квадрата, вписанного в ту же окружность.

1090. Сечение головки газового вентиля имеет форму правильного треугольника, сторона которого равна 3 см. Каким должен быть минимальный диаметр круглого железного стержня, из которого изготовляют вентиль?

1091. Поперечное сечение деревянного бруска является квадратом со стороной 6 см. Найдите наибольший диаметр круглого стержня, который можно выточить из этого бруска.

1092. Около окружности описаны квадрат и правильный шестиугольник. Найдите периметр квадрата, если периметр шестиугольника равен 48 см.

1093. Около правильного треугольника описана окружность радиуса R. Докажите, что R = 2r, где r — радиус окружности, вписанной в этот треугольник.

1094. Найдите площадь S правильного га-угольника, если: а) n = 4, R = 3√2 см; б) n = 3, Р = 24см; в) n = 6, r = 9см; г) n = 8, r = 5√3 см.

1095. Расстояние между параллельными гранями шестигранной головки болта, основание которого имеет форму правильного шестиугольника, равно 1,5 см. Найдите площадь основания.

1096. Стороны правильного треугольника, квадрата и правильного шестиугольника равны друг другу. Найдите отношения площадей этих многоугольников.

1097. Найдите отношение площадей двух правильных шестиугольников — вписанного в окружность и описанного около неё.

1098. Выразите сторону, периметр и площадь правильного треугольника: а) через радиус вписанной окружности; б) через радиус описанной окружности.

1099. Правильный восьмиугольник A₁A₂. A₈ вписан в окружность радиуса R. Докажите, что четырёхугольник А₃А₄А₇А₈ является прямоугольником, и выразите его площадь через R.

1100. С помощью циркуля и линейки в данную окружность впишите: а) правильный шестиугольник; б) правильный треугольник; в) квадрат; г) правильный восьмиугольник.

Ответы к задачам

1078. а) Да; б) нет.

1081. а) 60°; б) 108°; в) 120°; г) 144°; д) 160°.

1082. 360°. 1083. а) 3; б) 4; в) 8; г) 12.

1084. а) 6; б) 12; в) 4; г) 10; д) 20; е) 5.

1085. Указание. Воспользоваться тем, что серединный перпендикуляр к любой стороне правильного многоугольника проходит через центр описанной окружности.

1086. Указание. Воспользоваться тем, что биссектриса любого угла правильного многоугольника проходит через центр вписанной окружности.

1087.
1) R=3√2, r = 3, Р = 24, S = 36;
2) R = 2√2, а₄ = 4, Р = 16, S = 16;
3) r = 2√2, а₄ = 4√2, Р = 16√2, S = 32;
4) R = 3,5√2, r = 3,5, а₄ = 7, S = 49;
5) R = 2√2, r = 2, а₄ = 4, Р = 16.

1088.
1) r = 1,5, а₃ = 3√3, Р = 9√3,
2)
3) R = 4, а₃ = 4√3, Р = 12√3, S = 12√3;
4)
5), а₃ = 2, S = √3.

1094. a) 36 см 2 ; 6) 16√3 см 2 ; в) 162√3 см 2 ; r) ≈ 248,52 см 2 .

1095.

1098. a) 2√3r, 6√3r, 3√3r 2 ; б) √3R, 3√3R,

1100. в), г) Указание. Воспользоваться задачей 2, п. 113.