Углеродистая сталь модуль упругости

Модуль упругости разных материалов, включая сталь

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

• Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
• Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
• Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
• Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.

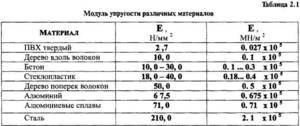
Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

• Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
• Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
• Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
• Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
• Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
• Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
• И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Модуль деформации стали и её упругости

Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.

Общие понятия

Модуль упругости (модуль Юнга) — это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения. Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).

Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.

Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях). Но инженеры на практике больше склоняются к применению размерности кгс/см2.

Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.

Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.

Механические свойства

Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:

1. Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
2. Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
3. Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
4. Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
5. Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
6. Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.

Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.

У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.

Модуль упругости

Стоит отметить, что эта величина непостоянная. Даже для одного материала она может иметь разное значение в зависимости от того, в какие точки была приложена сила. Кое-какие пластично-упругие материалы имеют практически постоянное значение модуля упругости при работе как на растяжение, так и на сжатие: сталь, алюминий, медь. А есть и такие ситуации, когда эта величина измеряется формой профиля.

Некоторые значения (величина представлена в миллионах кгс/см2):

1. Алюминий — 0,7.
2. Древесина поперёк волокон — 0,005.
3. Древесина вдоль волокон — 0,1.
4. Бетон — 0,02.
5. Каменная гранитная кладка — 0,09.
6. Каменная кирпичная кладка — 0,03.
7. Бронза — 1,00.
8. Латунь — 1,01.
9. Чугун серый — 1,16.
10. Чугун белый — 1,15.

Разница в показателях модулей упругости для сталей в зависимости от их марок:

1. Подшипниковые стали (ШХ-15) — 2,1.
2. Пружинные (60С2) и штамповые (9ХМФ) — 2,03.
3. Нержавеющие (12Х18Н10Т) — 2,1.
4. Низколегированные (40Х, 30ХГСА) — 2,05.
5. Обычного качества (Ст. 6, ст.3) — 2,00.
6. Конструкционные высокого качества (45,20) — 2,01.

Ещё это значение изменяется в зависимости от вида проката:

1. Трос с сердечником металлическим — 1,95.
2. Канат плетёный — 1,9.
3. Проволока высокой прочности — 2,1.

Как видно, отклонения в значениях модулей упругой деформации стали незначительны. Именно по этой причине большинство инженеров, проводя свои расчёты, пренебрегают погрешностями и берут значение, равное 2,00.

Модуль упругости стали

Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.

Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.

Общее понятие

Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).

В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.

Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.

Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.

Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.

Дополнительные характеристики механических свойств

Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:

• Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
• Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
• Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
• Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
• Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
• Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.

Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.

У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.

Значение модуля упругости

Необходимо заметить, что модуль Юнга не является постоянной величиной. Даже для одного и того же материала он может колебаться в зависимости от точек приложения силы.

Некоторые упруго — пластичные материалы обладают более или менее постоянным модулем упругости при работе как на сжатие, так и на растяжение: медь, алюминий, сталь. В других случаях упругость может изменяться исходя из формы профиля.

Вот примеры значений модуля Юнга (в миллионах кгссм2) некоторых материалов:

• Чугун белый – 1,15.
• Чугун серый -1,16.
• Латунь – 1,01.
• Бронза — 1,00.
• Кирпичная каменная кладка – 0,03.
• Гранитная каменная кладка – 0,09.
• Бетон – 0,02.
• Древесина вдоль волокон – 0,1.
• Древесина поперек волокон – 0,005.
• Алюминий – 0,7.

Рассмотрим разницу в показаниях между модулями упругости для сталей в зависимости от марки:

• Стали конструкционные высокого качества (20, 45) – 2,01.
• Стали обычного качества (Ст.3, Ст.6) — 2,00.
• Стали низколегированные (30ХГСА, 40Х) – 2,05.
• Стали нержавеющие (12Х18Н10Т) – 2,1.
• Стали штамповые (9ХМФ) – 2,03.
• Стали пружинные (60С2) – 2,03.
• Стали подшипниковые (ШХ15) – 2,1.

Также значение модуля упругости для сталей изменяется исходя из вида проката:

• Проволока высокой прочности – 2,1.
• Плетенный канат – 1,9.
• Трос с металлическим сердечником – 1,95.

Как видим, отклонения между сталями в значениях модулей упругой деформации имеют небольшую величину. Поэтому в большинстве инженерных расчетов можно пренебречь погрешностями и брать значение Е=2,0.

Расчетные сопротивления и модули упругости
для строительных материалов

При расчете строительных конструкций нужно знать расчетное сопротивление и модуль упругости для того или иного материала. Здесь представлены данные по основным строительным материалам.

Таблица 1. Модули упругости для основных строительных материалов

Нормативные данные для рассчетов железобетонных конструкций

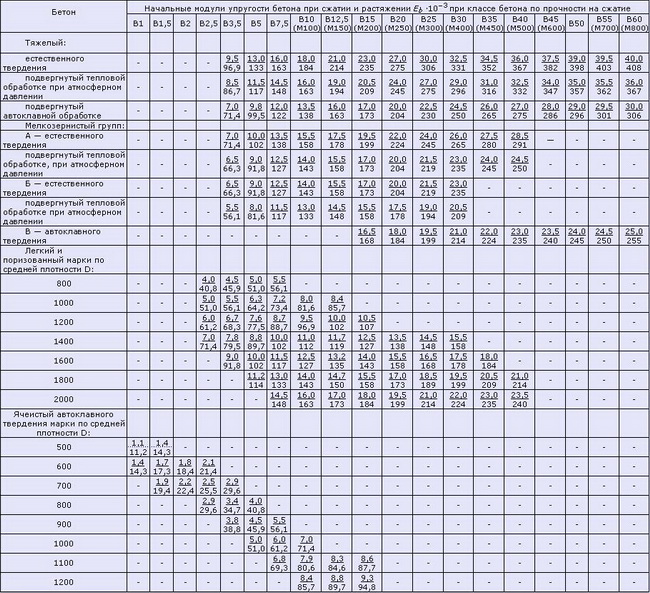
Таблица 2. Модули упругости бетона (согласно СП 52-101-2003)

Таблица 2.1 Модули упругости бетона согласно СНиП 2.03.01-84*(1996)

Примечания:
1. Над чертой указаны значения в МПа, под чертой — в кгс/см².
2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции.
3. Для ячеистого бетона неавтоклавного твердения значения Е_b принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8.
4. Для напрягающего бетона значения Е_b принимают как для тяжелого бетона с умножением на коэффициент
a = 0,56 + 0,006В.

Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)

Таблица 4. Расчетные значения сопротивления бетона сжатию (согласно СП 52-101-2003)

Таблица 4.1 Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)

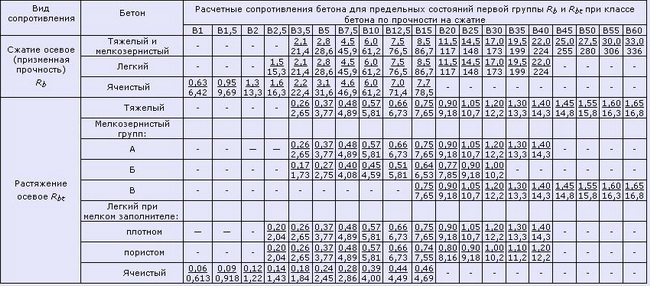
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)

Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)

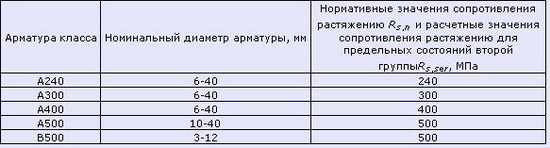
Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)

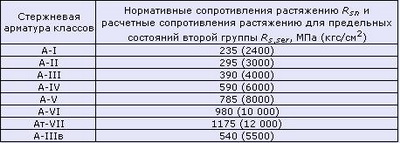
Таблица 6.2 Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)

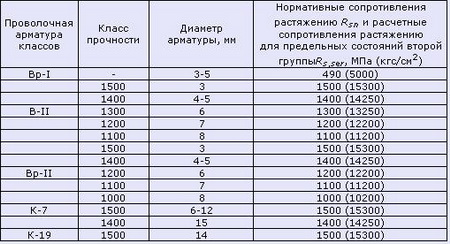
Таблица 7. Расчетные сопротивления для арматуры (согласно СП 52-101-2003)

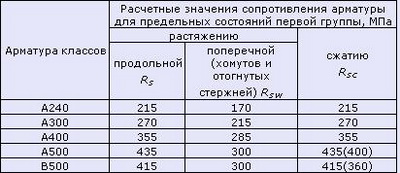
Таблица 7.1 Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)

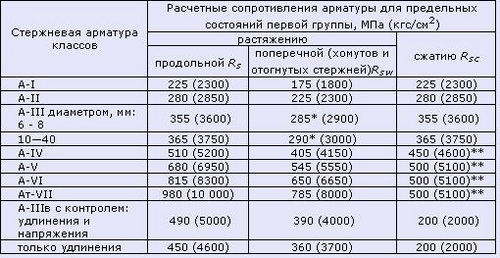
Таблица 7.2 Расчетные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)

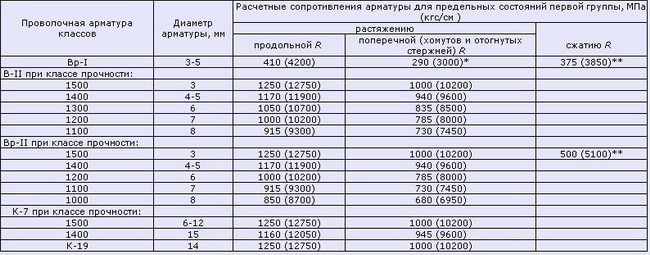
Нормативные данные для расчетов металлических контрукций

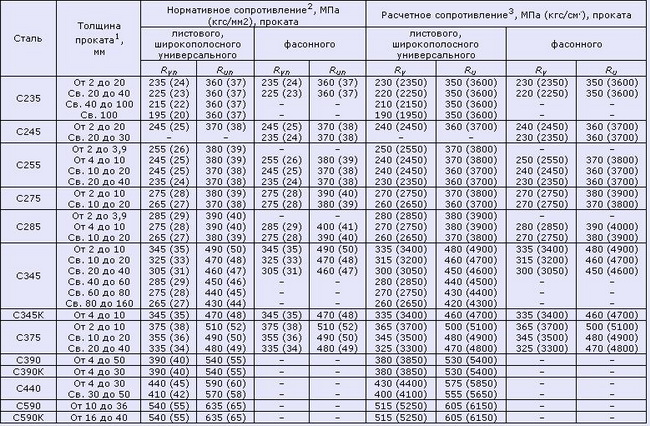
Таблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990)) листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений

Примечания:
1. За толщину фасонного проката следует принимать толщину полки (минимальная его толщина 4 мм).
2. За нормативное сопротивление приняты нормативные значения предела текучести и временного сопротивления по ГОСТ 27772-88.
3. Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, с округлением до 5 МПа (50 кгс/см²).

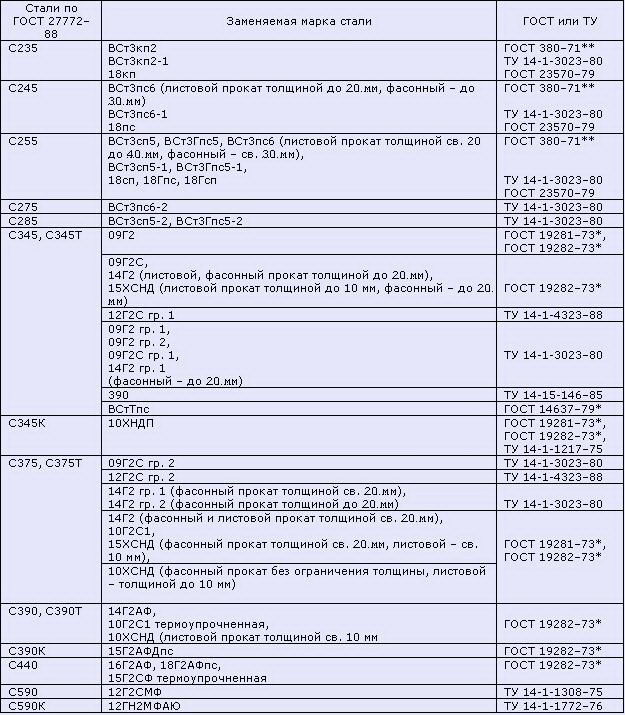
Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990))

Примечания:
1. Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*.
2. Стали С345К, С390, С390К, С440, С590, С590К по ГОСТ 27772-88 заменяют соответствующие марки стали категорий 1-15 по ГОСТ 19281-73* и ГОСТ 19282-73*, указанные в настоящей таблице.
3. Замена сталей по ГОСТ 27772-88 сталями, поставляемыми по другим государственным общесоюзным стандартам и техническим условиям, не предусмотрена.

Расчетные сопротивления для стали, используемой для производства профилированных листов здесь не показаны.

Модуль упругости сталей таблица

Упругие свойства тел

Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.

Модуль Юнга или модуль продольной упругости в дин/см 2 .

Модуль сдвига или модуль кручения G в дин/см 2 .

Модуль всестороннего сжатия или модуль объемной упругости К в дин/см 2 .

Объем сжимаемости k=1/K/.

Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.

Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:

K = E / 3(1 — 2μ) — (c)

Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.

Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона

Курсивом даны значения, вычисленные из соотношений (a), (b), (c).

Материал при 18°С

Модуль Юнга E, 10 11 дин/см 2 .

Модуль сдвига G, 10 11 дин/см 2 .

Коэффициент Пуассона µ

Модуль объемной упругости К, 10 11 дин/см 2 .

До того, как взять в работу какой-то строительный материал, необходимо изучить его прочностные данные и возможное взаимодействие с другими веществами и материалами, их сочетаемость в плане адекватного поведения при одинаковых нагрузках на конструкцию. Определяющая роль для решения этой задачи отводится модулю упругости – его называют ещё модулем Юнга.

Высокая прочность стали позволяет использовать её при строительстве высотных зданий и ажурных конструкций стадионов и мостов. Добавки в сталь некоторых веществ, влияющих на её качество, называют легированием, и эти добавки могут увеличить прочность стали в два раза. Модуль упругости стали легированной гораздо выше, чем обычной. Прочность в строительстве, как правило, достигается подбором площади сечения профиля в силу экономических причин: высоколегированные стали имеют более высокую стоимость.

Далее, будет рассмотрено значение термина, изменчивость его для стали различных сортов. Для сравнения будут приведены значения модуля других материалов.

Физический смысл

Обозначение модуля упругости как физической величины – (Е), этот показатель характеризует упругую сопротивляемость материала изделия прилагаемым к нему деформирующим нагрузкам:

• продольным – растягивающим и сжимающим;
• поперечным – изгибающим или исполненным в виде сдвига;
• объёмным – скручивающим.

Чем выше значение (Е), тем выше сопротивляемость материала нагрузкам, тем прочнее будет изделие из этого материала и тем выше будет предел разрушения. Например, для алюминия эта величина составляет 70 ГПа, для чугуна – 120, железа – 190, а для стали до 220 ГПа.

Определение

Модуль упругости – сводный термин, вобравший в себя другие физические показатели свойства упругости твёрдых материалов – под воздействием силы изменяться и обретать прежнюю форму после её прекращения, то есть, упруго деформироваться. Это отношение напряжения в изделии – давление силы на единицу площади, к упругой деформации (безразмерная величина, определяемая отношением размера изделия к его изначальному размеру). Отсюда и его размерность, как и у напряжения – отношение силы к единице площади. Поскольку напряжение в метрической СИ принято измерять в Паскалях, то и показатель прочности – тоже.

Существует и другое, не очень корректное определение: модуль упругости – это давление, способное удлинить изделие вдвое. Но предел текучести большого количества материалов значительно ниже прилагаемого давления.

Модули упругости, их виды

Способов изменения условий приложения силы и вызываемых при этом деформаций много, и это предполагает и большое количество видов модулей упругости, но на практике сообразно деформирующим нагрузкам выделяют три основных:

• Юнга (Е) представляет упругую сопротивляемость растягивающим и сжимающим нагрузкам – собственно, именно этим термином пользуются, когда говорят о модуле упругости;
• модуль сдвига (G) характеризует сопротивляемость любому нарушению формы без её разрушения или изменения нормы – это отношение сдвигающей нагрузки к деформации, проявляющейся в виде изменчивости прямого угла между двумя половинами плоскости, подвергшейся нагрузке. Второе название этого термина – жёсткости, он же представляет и вязкость материала;
• модуль объёмной упругости (К) – сопротивляемость изменению объёма при разносторонних нормально приложенных напряжениях, имеющих равную величину по всем векторам. Его называют ещё модулем объёмного сжатия, выражается отношением объёмного давления к объёмной деформации сжатия.

Этими показателями характеристики упругости не исчерпываются, есть и другие, которые несут другую информацию, имеют иную размерность и смысл. Это также широко известные среди специалистов показатели упругости Ламе и коэффициент Пуассона.

Как определить модуль упругости стали

Для определения параметров различных марок стали существуют специальные таблицы в составе нормативных документов в области строительства – в строительных нормах и правилах (СНиП) и государственных стандартах (ГОСТ). Так, модуль упругости (Е) или Юнга, у чугуна белого и серого от 115 до 160 ГПа, ковкого – 155. Что касается стали, то модуль упругости стали С245 – углеродистой имеет значения от 200 до 210 ГПа. Легированная сталь имеет показатели несколько выше – от 210 до 220 ГПа.

Та же самая характеристика у рядовых марок стали Ст.3 и Ст.5 имеет то же значение – 210 ГПа, а у стали Ст.45, 25Г2С и 30ХГС – 200 ГПа. Как видим, изменчивость (Е) для различных марок стали незначительна, а вот в изделиях, например, в канатах – другая картина:

• у прядей и свивок проволоки высокой прочности 200 ГПа;
• стальные тросы с металлическим стержнем 150 ГПа;
• стальные канаты с органическим сердечником 130 ГПа.

Как можно заметить, разница значительная.

Значения модуля сдвига или жёсткости (G) можно увидеть в тех же таблицах, они имеют меньшие значения, для прокатной стали – 84 ГПа, углеродистой и легированной – от 80 до 81 гпа, а для сталей Ст.3 и Ст.45–80 ГПа. Причиной различия значений параметра упругости является одновременное действие сразу трёх основных модулей, рассчитываемых по разным методикам. Однако разница между ними небольшая, что говорит о достаточной точности изучения упругости. Поэтому не стоит зацикливаться на вычислениях и формулах, а следует принять конкретную величину упругости и пользоваться ей как константой. Если не производить вычисления по отдельным модулям, а сделать расчёт комплексно, значение (Е) будет составлять 200 ГПа.

Необходимо понимать, значения эти разнятся для сталей с разными присадками и стальных изделий, включающих детали из других веществ, но разнятся эти значения незначительно. Основное влияние на показатель упругости оказывает содержание углерода, а вот способ обработки стали – горячий прокат или холодная штамповка, значительного влияния не оказывает.

При выборе стальных изделий пользуются также и ещё одним показателем, который регламентируется так же, как и модуль упругости в таблицах изданий ГОСТ и СНиП – это расчётное сопротивление растягивающим, сжимающим и изгибающим нагрузкам. Размерность у этого показателя та же, что и у модуля упругости, но значения на три порядка меньше. Этот показатель имеет два назначения: нормативное и расчётное сопротивление, названия сами говорят за себя – расчётное сопротивление применяется при выполнении расчётов прочности конструкций. Так, расчётное сопротивление стали С255 при толщине проката от 10 до 20 мм – 240 МПа, при нормативном 245 МПа. Расчётное сопротивление проката от 20 до 30 мм чуть ниже и составляет 230 МПа.

Физические характеристики материалов для стальных конструкций

проката и стальных отливок

отливок из чугуна

Коэффициент линейного расширения α, ºC -1

прокатной стали и стальных отливок

отливок из чугуна марок:

пучков и прядей параллельных проволок

спиральных и закрытых несущих

двойной свивки с неметаллическим сердечником

Модуль сдвига прокатной стали и стальных отливок G, МПа (кгс/см 2 )

Коэффициент поперечной деформации (Пуассона) ν

Примечание. Значения модуля упругости даны для канатов, предварительно вытянутых усилием не менее 60 % разрывного усилия для каната в целом.

Физические характеристики проводов и проволоки

Марка и номинальное сечение, мм 2

Коэффициент линейного расширения α; ºС -1

Алюминиевые провода по ГОСТ 839-80*Е

Способы определения и контроля показателей прочности металлов

Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.

Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.

Виды нагрузок

При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.

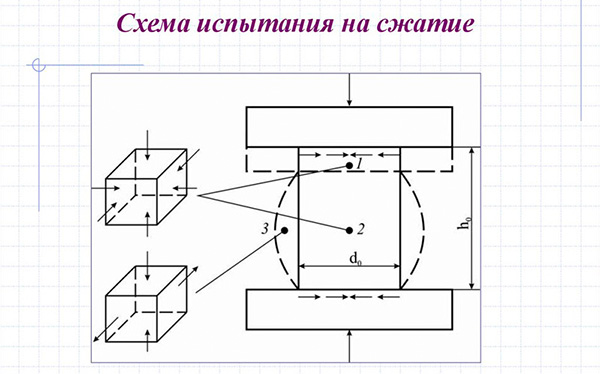
• Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.

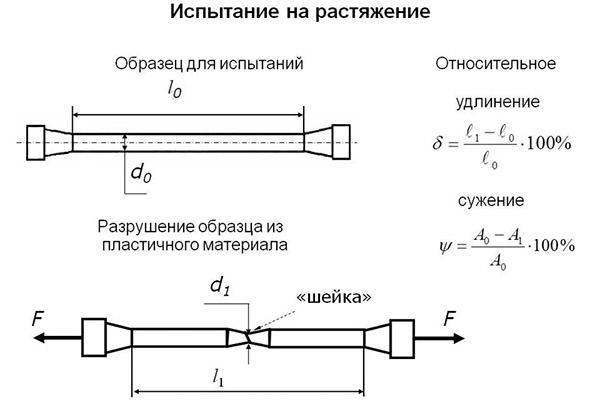
• Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.

• Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.

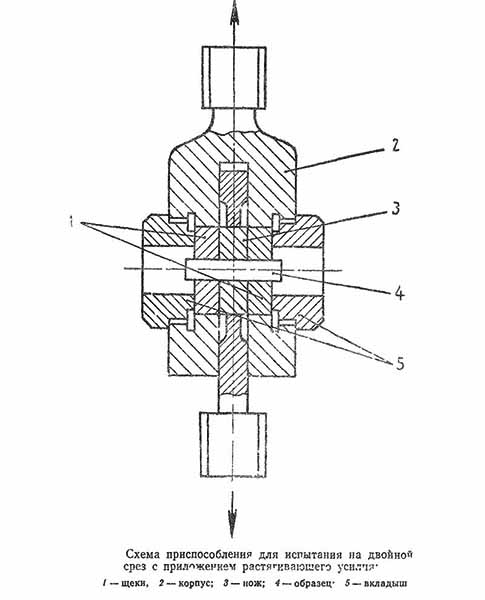
• Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.

• Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

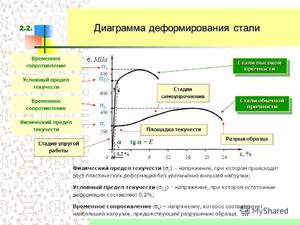
Понятие о модуле упругости

В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:

1. Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
2. Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).

Формула по закону Гука записывается в виде ε = σz/E, где:

• ε – относительное удлинение;
• σz – нормальное напряжение.

Демонстрация закона Гука для упругих тел:

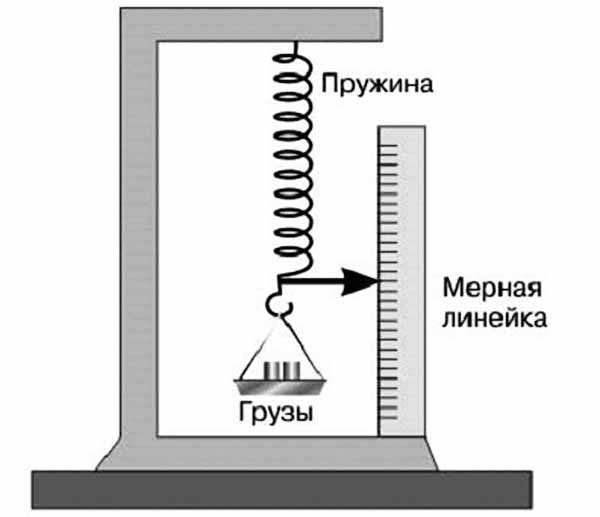
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.

В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.

Значения модуля упругости для некоторых материалов приведены в таблице 1.