Рычажные механизмы примеры решения

6 Кинематический анализ рычажных механизмов

4. Кинематический анализ рычажных механизмов

Кинематический анализ механизмов включает вопросы изучения звеньев с геометрической точки зрения, т.е. без учета действующих сил. Для этого используются графические, аналитические и экспериментальные методы исследования.

Одним из наглядных методов является графоаналитический, который включает:

а) построение планов положения механизма; б) определение скоростей и ускорений характерных точек или звеньев механизма.

При графических построениях на чертеже изображаются длины звеньев, скорости, ускорения и др. величины в определенном масштабе, характеризуемом масштабным коэффициентом:

m=значение параметра/длина отрезка.

Например, вектор pa длиной 10 мм изображает скорость V=20 м/с. Тогда m_v=20/10=2 м·с -1 /мм.

4.1. Построение планов положения механизма

Графическое изображение взаимного расположения звеньев механизма, соответствующее заданному моменту времени, называется планом положений или планом механизма.

Планы положения строятся в определенном масштабе методом засечек в соответствии с формулой строения механизма, При этом должны быть заданы линейные размеры всех звеньев (рис.14).

После построения нескольких совмещенных планов механизма

Рис. 14 при необходимости можно определить графически траектории характерных точек звеньев, имеющих сложное движение, например, центра тяжести S шатуна AB (рис.14).

4.2. Определение скоростей и ускорений механизма методом планов

Метод планов является одним из самых наглядных. Определению подлежат линейные скорости и ускорения отдельных точек и угловые скорости и ускорения звеньев. При этом предварительно составляются векторные уравнения для скоростей и ускорений точек звеньев, совершающих сложное движение, например:

а) звено совершает плоскопараллельное движение, состоящее из переносного, т.е. поступательного со скоростью полюса и относительного вращательного вокруг полюса (рис.15).

Принимая за полюс т. A, получим:

V_B=V_A+V_BA; где V_BA=w·l_AB;

a_B=a_A+a_BA; где a_BA=a n _BA+a t _BA при

Здесь V, a, w, e — линейные скорости и ускорения соответствующих характерных точек, а также угловые скорость и уско-

рение звена (индексы соответствуют ха-

рактеру ускорений и обозначениям точек).

б) звено совершает сложное движение, состоящее из переносного вращательного и относительного поступательного, например, звено 1 (рис.16).

Пусть B₁ и B₂ – точки, принадлежащие звеньям 1 и 2. Тогда:

V_B1=V_B2+V_B1B2, где V_B2=w·l_AB.

a_B1=a_B2+a t _B1B2+a k _B1B2, где ускорение Кориолиса

a k _B1B2=2V_B1B2·w и совпадает с направлением вектора V_B1B2, повернутого на 90 ○ в сторону переносного вращения.

Решение векторных уравнений осуществляется графически путем построения так называемых планов скоростей и ускорений, на которых абсолютные скорости и ускорения откладываются от одной точки, называемой полюсом, в определенном масштабе.

Пример расчета кривошипно-ползунного механизма рассмотрен на рис.17, где план положений (рис.17, а), план скоростей и ускорений (рис.17, б, в).

Векторные уравнения для скоростей записываются в виде:

V_B=V_A+V_BA; V_B=V_Bx+V_BBx;

т.е. в выбранном масштабе μ_V: pb||x-x; ab_|_AB

Векторные уравнения для ускорений при w₁=const записываются в виде:

a_B=a_A+a_BA; a_B=a_Bx+a k _BBx+a t _BBx; где a_A=a n _A=w₁ 2 ·l_OA; a_BA=a n _BA+a t _BA;

Все ускорения представлены на рис.17 в выбранном масштабе μ_a в виде соответствующих отрезков, например, a_B=μ_a·πb и т.д.

отрезок ca на плане скоростей соответствует V_CA_|_CA;

отрезок ab на плане скоростей соответствует V_AB_|_AB;

отрезок bc на плане скоростей соответствует V_BC_|_BC;

т.е. треугольник abc подобен треугольнику ABC.

Ускорения относительного (вращательного) движения равны:

; ; ,

Следовательно, треугольник abc подобен треугольнику ABC. Аналогичным является построение фигур для любой промежуточной точки, например т. S (рис.18, а, б).

4.3. Исследование рычажных механизмов методом

Кинематической диаграммой называется графическая зависимость какого-либо параметра движения звена от времени или от перемещения входного звена, представленные в определенной системе координат.

Если известна одна кинематическая диаграмма, то можно получить остальные зависимости путем графического дифференцирования или интегрирования.

На рис.19, а, б показана последовательность построе­ния кинематической диа­граммы перемещения ползуна кривошипно-ползунного меха­низма S(φ) и S(t), а также эле­менты графического дифферен­цирования с получе­нием диаграммы скоростей V(t) методом хорд.

Если диаграмма V(t) пер­вична, то процесс, обратный интегрированию, обеспечит получение диаграммы S(t) и называется графическим интег-рированием.

Следует отметить, что графические методы часто приводят к искажениям резуль-

Рис. 19 татов из-за неточности графических построений, поэтому необходимо контролировать расположение характерных точек, соответствующих экстремумам на диаграммах.

4.4. Кинематическое исследование рычажных механизмов

Аналитические методы исследования позволяют проводить анализ с заданной степенью точности. Кроме того, создание математических моделей механизмов позволяет решать задачи их оптимального синтеза при использовании ЭВМ.

Рассмотрим пример кинематического исследования синусного механизма (механизм двойного ползуна), где кривошип 1 вращается с угловой скоростью ω и угловым ускорением ε (рис.20).

Тогда скорость и ускорение точки А равны:

V_A=l_OA·ω; .

Все точки звена 1 и 2 описывают окружности, а точки звена 3 движутся поступательно, имея перемещения, скорости и ускорения равные:

При исследовании многих механизмов получаются достаточно громоздкие формулы, что не является препятствием при использовании ЭВМ.

При исследовании пространственных механизмов используются элементы векторной алгебры и векторного анализа. Положения, скорости и ускорения точек механизма выражаются в векторной форме, при необходимости вычисляются проекции на оси и плоскости. Примеры таких исследований изложены в учебной литературе.

Пример силового расчета рычажного механизма

Известны графические методы силового расчета механизмов. Однако в последнее время более широко применяют аналитические методы.

Аналитический метод рассмотрим на примере центрального кривошипно-ползунного механизма [3].

Исходные данные: 1) кинематическая схема (рис. 4.6); 2) массы и моменты инерции звеньев, положения их центров масс; 3) закон движения механизма; 4) внешнее силовое нагружение и М. Зависимости /^((pi), A/i(9 i) и закон движения со/ = a>(

Зададим систему координат Аху (рис. 4.6). Необходимые для силового расчета кинематические характеристики:

Рис. 4.6. Схема кривошипно-ползунного механизма

В этих уравнениях co_(/i = — cos q /y^cos (fh — аналог угловой скорости (передаточная функция) звена 2; Sq₂

аналог углового ускорения звена 2:

а Способ определения углового ускорения ?| начального звена 1 описан ранее.

Следуя общепринятой методике, получим:

где

При установившемся движении с малым коэффициентом неравномерности можно принять coi

0. Тогда после преобразований и упрощений уравнения (4.7) проекция ускорения асх примет вид:

Определим проекции главных векторов сил инерции и главные моменты сил инерции, заметив, что a_Cv — 0, е₃ = 0 (рис. 4.6):

Главный вектор сил инерции звена 1 Ф| = -m_xa_S =0, так как asi = 0, поскольку центр масс Si благодаря противовесу находится на оси вращения А (рис. 4.6).

Как следует из уравнений (4.7) — (4.13), величины главных векторов и главных моментов сил инерции существенно зависят от квадрата угловой скорости wf , начального звена /, что имеет особое значение для быстроходных механизмов.

В уравнении (4.11) приведено приближенное выражение для проекции асху вполне пригодное для практических расчетов применительно к установившемуся режиму. Как видно, эта проекция, а следовательно, и проекция Ф_3у являются функциями нс только угла ф! , но и двойного угла 2q>j. Поэтому первое слагаемое в выражении силы инерции Ф₃ = Ф_3д (если раскрыть скобки) периодически изменяется с частотой вращения звена 1 и называется силой инерции первого порядка. Второе слагаемое периодически изменяется с двойной частотой и называется силой инерции второго порядка.

Расчленив механизм, перейдем к силовому расчету сгрукгурной группы 2-3. К ее звеньям приложены следующие известные внешние силы: F₃, Ф₃, Ф₂ и момент М_ф2 (рис. 4.7, а). Неизвестными являются модуль и направление силы F₁₂, модуль силы F₃₄ и ее плечо b, модуль и направление сил взаимодействия в шарнире С, связанных соотношением F₂₃ = -F₃₂.

Рис. 4.7. Схема усилий структурной группы 2-3

Сумма проекций на ось х сил, приложенных к звеньям 2 и 3, равна нулю: Следовательно,

Из уравнения (4.14) определяется проекция f₂ 1, Знаки в этом уравнении, как и во всех последующих, имеют алгебраический смысл. Это значит, что числовые значения известных проекций сил подставляются в уравнения проекций и моментов со строгим соблюдением их знаков. Так, проекция F& имеет знак минус, поскольку сила направлена вниз (рис. 4.7, а). Модуль и направление силы F, надо взять из исходных данных. Величины и знаки проекций Ф_1х и Ф_3д определяются в результате расчетов по уравнениям (4.9), (4.7) и (4.12).

Сумма гтоекций на ось * сил, приложенных к звену 5, равна нулю: , или

откуда определяем проекцию F_i2x.

Для определения проекции F^y используем уравнение моментов для звена 2 (относительно точки В) Отсюда

В этом уравнении

Модуль силы F₂3, нагружающей шарнир С, найдем из уравнения:

а угловую координату (р/^₃ вектора F₂$ — через sin ! = 0, уравнения проекций сил, приложенных к звену У, т.е. приобретают такой вид:

откуда

Составим уравнение моментов для звена У относительно точки А:

Момент M_a(f_x>) подставляется в уравнение с тем знаком, который он получает при подсчете по формуле M_a(f₁₂) = F_2yl_AB cos Ф1 — F2xIab sin

Уравнение (4.22) является контрольным, поскольку все три слагаемых в его левой части известны. Однако оно может быть и расчетным, например, когда силовой анализ выполняется для механизма, движущегося в установившемся режиме с малым коэффициентом неравномерности. В этом случае момент М_ф обычно неизвестен и его надо определить из уравнения (4.22). Момент А/_ф| может иметь значительную величину, что весьма существенно для расчета главного вала машины (звена У) на прочность.

При малой неравномерности вращения звена У его угловое ускорение Е в начале расчета часто не определяют, поскольку оно весьма мало. Однако принять вследствие этого Л/_ф1 = -&J_A

0 никак нельзя. Неравенство момента М_ф нулю вытекает из уравнения (4.22), поскольку моменты М и M_A(F₂) заведомо неравны и сильно отличаются друг от друга. Большое значение М_ф при очень малом значении Gi объясняется следующим: чем с меньшим угловым ускорением Ei должно вращаться звено /, тем большим должен быть момент инерции J_A этого звена; поэтому произведение весьма малой величины Е на весьма большую J_Ay т.е. |ej J_A = М_ф, отнюдь не мало.

Определим силовые факторы, нагружающие корпус машины и ее основание. Рассмотрим стойку кривошипно-ползунного механизма (рис. 4.9). Конструктивно это корпус машины, который устанавливается на специальном основании. Если машина — автомобильный ДВС, то таким основанием будет рама автомобиля, если — стационарный компрессор или пресс, то — фундамент, на котором установлен компрессор или пресс и т.д.

Рис. 4.9. Схема стойки кривошипно-ползунного механизма

К стойке 4 приложены следующие силы и моменты (рис. 4.9, а): ставшие известными воздействия звена 1 F₄₁ =—и звена 3 F₄з =-/^4, сила F_4p =-F$, зависящая от рабочего процесса машины, и, наконец, реакция основания, представленная в виде двух силовых факторов, а именно — неизвестного но модулю и направлению главного вектора F₄ и неизвестного главного момента М₄. Условимся определять величину главного момента Л/₄, полагая, что линия действия главного вектора F₄ проходит через точку А. Напомним, что в перечисление сил, действующих на стойку, как и ранее условно не включена ее сила тяжести.

Если силовой расчет выполняется для кривошипно-ползунного механизма поршневой машины (насоса, компрессора, детандера, ДВС и т.п.), то сила F_4p является силой давления рабочего тела (жидкости,

газа), находящегося внутри цилиндра Ц, на его крышку К (рис. 4.9, б). Если кривошипно-ползунный механизм — главный механизм пресса или станка, то силой /^является то воздействие, которое обрабатываемое изделие оказывает на стол пресса или станка.

Составим векторное уравнение равновесия стойки

представленное графически на рис. 4.9, в. Используя соотношения

, получим Но

из плана сил (рис. 4.7, б) следует:

Поэтому или в проекциях:

F₄ = —Ф₂у • Отсюда определяем и угловую координату ф/.₄ вектора

Сила F₄з создаст относительно точки А момент M_A(F₄₃) (рис. 4.9, а). Уравновешивает его только реактивный момент М₄, действующий от основания на корпус (на стойку), так как остальные силы, прило-женные к стойке, момента относительно точки А не создают. Момент M_A(F₄3) стремится опрокинуть корпус машины. Величину момента М₄, препятствующего этому опрокидыванию, определим из уравне-ния равновесия стойки M_A(F_47>) + М₄ = 0, откуда

Опрокидывание испытывает корпус и компрессора, и ДВС, и электродвигателя, т.е. любой машины, независимо от того, какой рабочий процесс в ней протекает. Опрокидывание испытывает также любой передаточный механизм. Поэтому машину и передаточный механизм всегда надо надежно закреплять на их основании. Конструктивное исполнение этого закрепления и методика его расчета излагаются в курсе «Детали машин» и в специальных машиностроительных курсах.

Выразим искомый момент М₄ по-иному. Для этого составим уравнение моментов относительно точки А для всех четырех звеньев (рис. 4.7, а; 4.8; 4.9, а), т.е. для механизма в целом. Заметим, что моменты сил взаимодействия F₂₃ и F₃₂ в шарнире С равны и противоположны друг другу (рис. 4.7, а), а потому в уравнение моментов не войдут. То же самое относится к моментам сил взаимодействия во всех остальных кинематических парах, т.е. сил, являющихся внутренними для механизма в целом. Следовательно, в уравнение войдут только моменты сил и пар сил, приложенных к механизму извне (рис. 4.9, б). Поэтому для механизма в целом оно примет вид:

Из выражения (4.23) следует, что величина искомого момента М₄ определяется внешним активным моментом Л/_ь приложенным к валу машины (т.е. к звену 1 механизма), а также влиянием ускоренного движения звеньев. Это влияние численно оценивается посредством момента главного вектора и главных моментов сил инерции, поскольку силовой расчет проводится методом кинетостатики (формула 4.1).

Определим, какое давление на свое основание (фундамент) оказывает машина, механизмом которой является кривошипно- ползунный. Систему нагружения основания со стороны машины можно свести к главному вектору F₀ = -F₄, линия действия которого проходит через точку А (ось вращения звена /, т.е. вал машины), и к главному моменту М₀ = —М₄ (рис. 4.9, г).

Проекции главного вектора F_a на оси х и у:

Главный момент M_Q выразится так:

В уравнениях (4.24) — (4.26) буквами Фу и М_ф? обозначены общий

главный вектор (через его проекции) и общий главный момент системы сил инерции всех подвижных звеньев механизма. Члены

Ф_уУ Мд(Ф) входят в состав этих уравнений в том случае, когда центр масс звена 1 не находится на его оси вращения; слагаемые Фъу= о, М_А(ф_ъ)= О (рис. 4.7, а), М_ф> = 0 [см. уравнение (4.13)].

Как видно из уравнений (4.24) и (4.25), главный вектор F₀ вычисляется посредством сил инерции, а это указывает на то, что он есть результат ускоренного движения всех подвижных звеньев механизма, т.е. имеет динамическую природу. Отмстим, что на основание машины передастся также воздействие ее силы тяжести и в ряде случаев воздействия других активных сил (например, сил затяжки фундаментальных болтов), которые в силовом расчете не рассматривались. Следовательно, в общем случае главный вектор F₀ содержит две составляющие: во-первых, динамическую составляющую, вызванную ускоренным движением звеньев механизма, и, во- вторых, составляющую, вызванную действием активных сил.

Главный момент М₀ в общем случае складывается также из двух составляющих: во-первых, из динамической составляющей, являющейся результатом ускоренного движения звеньев [см., например, квадратные скобки в уравнении (4.26)], и, во-вторых, из составляющей, вызванной действием активных сил и моментов.

Расчет рычажного механизма (стр. 1 из 4)

Министерство образования Российской Федерации

Рыбинская государственная авиационная

Кафедра «Основы конструирования машин»

1 Структурный анализ и геометрический синтез рычажного механизма

Структурная схема рычажного механизма, показанная на рис. 1

Рисунок 1 – Структурная схема механизма

Размеры коромысла: l_BE = 0,6 м; y = 0,2 м;

Углового размаха коромысла ψ = 55 0 .

Входное звено – кривошип.

Коэффициент изменения средней скорости выходного звена k = 1,07.

Максимальные углы давления в кинематических парах В и D δ max = 38 0 .

Направление действия силы полезного сопротивления F _ПС — по стрелке.

Угловая скорость кривошипа: w ₁ =12 рад/с.

Значение силы полезного сопротивления: F пс=3000Н.

Модуль зубчатого зацепления: m=30 мм.

Числа зубьев колёс: Z 1=16, Z 2=20.

2 Структурный анализ рычажного механизма

Вычерчиваем структурную схему механизма и указываем на ней номера и наименования звеньев. Звено 5 является выходным, так как к нему приложена сила полезного сопротивления F _ПС .

Рисунок 2 – Структурная схема механизма: 1 – кривошип; 2, 4 – шатуны; 3-коромысло; 5 – ползун; 6 – стойка.

Составляем таблицу кинематических пар

Таблица 1 – Таблица кинематических пар

Определяем число степеней подвижности механизма по формуле Чебышева

где n = 5 – число подвижных звеньев (см. рис. 2);

p ₅ = 7 – количество пар 5 класса (см. табл. 1);

p ₄ = 0 – количество пар 4 класса (см. табл. 1);

q _ПС = 0 – число пассивных связей. В рассматриваемом механизме нельзя отбросить ни одно из звеньев так, чтобы это не сказалось на законе движения выходного звена.

Подставляем значения в формулу (1) и выполняем вычисления.

W = 3 · 5 – 2 ·7 = 1

В механизме одно входное звено.

Расчленяем механизм на простейшие структурные составляющие.

Формула строения I (1,6) → II (2,3) → II (4,5)

Механизм в целом относится ко второму классу.

3. Определение недостающих размеров звеньев

Размер звеньев будем определять графоаналитическим методом.

Для построения планов механизма выберем стандартный масштабный коэффициент длины μ₁ = 0,01 м / мм.

Определяем длины отрезков на планах, соответствующие звену 3.

Вычерчиваем планы звена 3 в крайних положениях, выдерживая между ними угол размаха ψ = 55 0 (рисунок 4). Крайнее правое положение в дальнейшем будем обозначать верхним индексом К 1, а крайнее левое – К 2.

Из точки В проводим вектор её скорости V_B . Ввиду того, что звено 3 совершает вращательное движение вокруг точки Е , он направлен перпендикулярно ВЕ.

Вследствие расположения центра вращения кривошипа (точка О) слева от коромысла угол давления δ max _вр принимает наибольшее значение, равное 38° , в положении К 1. Проводим под этим углом к вектору V _В прямую В k 1 N 1 , по которой направлены звенья 1 и 2 в этом положении.

Вычисляем величину угла перекрытия:

Из точки В k 2 проводим вспомогательную прямую В k 2 Н, параллельную В k 1 N 1 .

Строим угол НВ k 2 N 2 , равный Θ, и проводим прямую В k 2 N 2 , пресекающую В k 1 N 1 .

Точка О, в которой пересеклись прямые, и является центром вращения кривошипа. Изображаем соответствующий элемент стойки.

Для определения размеров на плане отрезков, соответствующих звеньям 1 и 2, составляем и решаем систему уравнений.

Наносим на план механизма точки А k 1 и А k 2.

Вычисляем реальные размеры звеньев

Центр вращения кривошипа смещен относительно направляющей стойки на величину y=0,2 м.

Параллельно направляющей, на высоте y, проводим прямую E * R.

Проводим пунктирной линией перпендикуляр ЕВ * к направляющей, равный

ЕВ * =ЕВ к1 =ЕВ к2 или ЕС * =ЕС к1 =ЕС к2 .

Из точки С * опускаем штрих пунктирную прямую под углом d max = 38 0 к направляющей E * R. Точка пересечения D * . Длину прямой вычисляем графическим способом С * D * =0.65 м.

Из точек С к1 и С к2 опускаем прямые к прямой E * R равные С к1 D k 1 =C * D * =C k 2 D k 2 =0.65 м. Соответственно точки пересечения D k 1 и D k 2 .

Получим отрезки ½С к1 D k 1 ½ и ½С к2 D k 2 ½, соответствующие шатуну в крайних положениях к1 и к2.

Вычерчиваем звено 5 в крайних положениях.

Вычисляем длину шатуна 4.

4. Определение направления вращения кривошипа

Строим траектории центров шарниров. Для точек А, В и С это – дуги окружностей радиусов соответственно |ОА|, |ВЕ | и |ЕС |. Кривошип 1 совершает полный оборот и поэтому точка А движется по окружности. Точка D вместе с ползуном 5 перемещается по прямой E * R.

Вычисляем углы поворота кривошипа, соответствующие рабочему и холостому ходам, и проставляем их на планах.

αр = 180˚ + Θ = 180˚+ 6˚5΄ = 186˚5΄

αх = 180˚ – Θ = 180˚ – 6˚5΄ = 173˚55΄

Во время рабочего хода ползун 5 движется против силы F _ПС из положения К2 в положение К1 . При этом шарнир С перемещается по дуге окружности из положения С k 2 в положение С k 1

Точка А , расположенная на кривошипе 1, должна в течении рабочего хода переместиться из положения А k 2 в положение А k 1 , а сам кривошип – повернуться на угол

Проставляем найденное направление угловой скорости на планах механизма.

5. Подготовка исходных данных для введения в ЭВМ

Изображаем расчетную схему для вывода формул, связывающих некоторые геометрические параметры механизма.

Рисунок 5 – расчетная схема

Из чертежа видно t=180 0 – g + b Так как угол b отсутствует, следует что b = 0, а значит Sinb = 0 и z=y

Взяв геометрические размеры из пунктов 1.2, 1.3, 3.13, 3.20 и значение угловой скорости из пункта 1.9, составляем таблицу исходных данных для введения в ЭВМ.

Введение

Механизмы, входящие в состав любой машины или прибора, весьма разнообразны. С точки зрения их функционального назначения они делятся, на следующие виды: механизмы двигателей и преобразователей, придаточные и т.д. В зависимости от конструктивных особенностей и способа передачи движения между подвижными звеньями механизма делят на:

Шарнирно-рычажные; фрикционные; зубчатые; кулачковые; винтовые; с гибкими звеньями.

Шарнирно-рычажные механизмы

Шарнирный механизм, механизм, звенья которого образуют только вращательные кинематические пары (шарниры).

Шарнирный механизм подразделяется на плоские, сферические и пространственные общего вида. В плоских, шарнирный механизм оси шарниров параллельны, и поэтому все звенья совершают плоскопараллельное движение. Простейший плоский шарнирный механизм состоит из 4 звеньев и называется шарнирным четырехзвенником . В сферической, шарнирный механизм оси шарниров пересекаются в одной точке. Наименьшее число звеньев сферического шарнирного механизма так же равно 4 . Сферический четырехзвенник ( рис. 1) применяется, например, в многопоршневых насосах и в устройствах стабилизации летательных аппаратов.

Частный случай сферического четырехзвенника ,в котором оси двух вращательных пар взаимно перпендикулярны — карданным механизмам. В пространственном, шарнирный механизм оси вращательных пар скрещиваются под различными углами. В общем случае пространств, шарнирный механизм должен иметь не менее 7 звеньев (пространственный семизвенник ). Однако при выполнении определенных соотношений между линейными и угловыми размерами звеньев, минимальное число звеньев уменьшается до 4 (например, механизм Беннета). Шарнирный механизм применяется в с/х машинах, машинах-автоматах, (например, в легковой и пищевой промышленности) и т. д.

По способу задания требуемого движения рабочего звена, шарнирный механизм делятся на: перемещающие, направляющие передаточные и механизм для движения с остановками. Перемещающие шарнирные механизмы предназначены для перемещения рабочего звена из одного положения в другое.

Задачи структурного анализа механизма

Задачей структурного анализа механизма является задача определения параметров структуры заданного механизма — числа звеньев и структурных групп, числа и вида КП, числа подвижностей (основных и местных), числа контуров и числа избыточных связей.

Основные понятия структурного понятия

Механизм — механическая система, предназначена для преобразования движения одного или нескольких тел требуемые движения других тел.

Подвижное звено механизма — твердое тело входящие в состав механизма.

Стойка — звено, принимаемое за неподвижное.

Ведущие (входное) звено — звено соединенное с источником энергии, которому сообщается движение, преобразуемое механизмом в требуемое движение других звеньев.

Ведомое (выходное) звено — звено, совершающие движение, для выполнения которого предназначен механизм.

Начальное звено — звено, которому приписывается одна или несколько обобщенных координат механизма.

Обобщение координат механизма — каждая из независимых между собой координат, определяющая положение всех звеньев механизма относительно стойки.

Кинематическая пара — соединение двух соприкасающихся звеньев, допускающих их относительное движение.

Элемент кинематической пары — совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару.

Кинематическая цепь — система звеньев, связанных между собой кинематическими парами.

Замкнутая кинематическая цепь — кинематическая цепь, звенья которой они образует один или несколько замкнутых контуров.

Незамкнутая кинематическая цепь — кинематическая цепь, звенья которой не образуют замкнутых контуров.

Структурная схема механизма — схема механизма, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение.

Класс кинематической пары — число связей, наложенных на относительное движение звеньев.

Поступательная пара — одноподвижная пара, допускающая прямоленейно-поступательное движение одного звена относительно другого.

Вращательная пара — одноподвижная пара, допускающая вращательное движение одного звена относительно другого.

Низшая пара — кинематическая пара, в которой требуемое относительное движение звеньев может быть получено постоянным соприкасанием ее элементов по поверхности.

Высшая пара — кинематическая пара, в которой требуемое относительное движение звеньев может быть получено только соприкасанием ее элементов по линиям и в точках.

Плоский механизм — механизм, подвижные звенья которого совершают плоское движение, параллельное одной и той же неподвижной плоскости.

Рычажный механизм — механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары.

Шарнирный механизм-механизм, звенья которого образуют только вращательные пары.

Кривошип — вращающееся звено рычажного механизма, которое может совершать полный оборот вокруг неподвижной оси.

Коромысло — вращающееся звено рычажного механизма, которое может совершать только не полный оборот вокруг неподвижной оси.

Шатун — звено рычажного механизма, образующие кинематические пары только с подвижными звеньями.

Ползун — звено рычажного механизма, образующие поступательную пару со стойкой.

Кулиса — звено рычажного механизма, вращающееся вокруг неподвижной оси и образующие с другим подвижным звеном поступательную пару.

Кинематический анализ механизма — определение движение звеньев механизма по заданному движению начальных звеньев.

Кинематическая схема механизма — структурная схема механизма с указанием размеров звеньев, необходимых для кинематического анализа механизма.

Крайнее положение звена — положение звена, из которого оно может двигаться только в одном направление.

Крайнее положение механизма — положение механизма, при котором хотя бы одно звено занимает крайнее положение.

Масштабный коэффициент — отношение численного значения физической величины в свойственных ей единицах к длине отрезка в миллиметрах, изображающего эту величину (на схеме, графике и т.д.).

Структурный анализ плоских рычажных механизмов

Механизмы делятся на классы. Класс механизма определяется наивысшим классом структурный группы, входящей в состав механизма. Класс механизма зависит от того, какое звено является входным.

Чтобы определить, из каких групп Асура составлен механизм, рекомендуется поступать следующим образом. Сначала надо попытаться отсоединить от механизма простейшую группу Ассура 2 класса, состоящую из двух звеньев и трех кинематических пар (если можно присоединить группу без изменения степени подвижности, то можно и отсоединить). Оставшаяся кинематическая цепь должна остаться замкнутой и тоже быть механизмом с первоначальным значением подвижности W. Если отсоединить группу 2 класса невозможно, следует попытаться отсоединить группу 3 класса и т. д. После отсоединения одной группы нужно перейти к отсоединению следующих групп, придерживаясь указанной последовательности. После отсоединения всех групп Ассура, входящих в состав механизма, должен остаться исходный механизм (механизм I класса) Затем записать формулу строения механизма (рис.2). На рис.2 показан пример образования плоского рычажного механизма. К исходному механизму, состоящему из стойки (нулевое звено) и входного звена 1, присоединена группа Ассура II класса 2-го порядка, состоящая из двух звеньев (второго и третьего); затем была присоединена аналогичная группа, состоящая из 4-го и 5-го звеньев.

На рис. 2д показана формула строения механизма, представляющая собой закодированную запись образования механизма: а – исходный механизм, состоящий из стойки и входного звена 1; б – структурная группа II класса 2-го порядка, состоящая из звеньев 2 и 3; в – структурная группа II класса 2-го порядка, состоящая из звеньев 4 и 5.

1.4. Структурный анализ плоских рычажных механизмов

Под структурным анализом понимают определение количества звеньев и кинематических пар, классификацию кинематических пар, определение степени подвижности механизма, класса и порядка механизма.

Умение проводить структурный анализ механизма имеет большое значение для дальнейшего изучение курса, так как структура механизма определяет последовательность и методы кинематического и силового ( кинетостатического ) исследования механизма.

Пример 1. Определить степень подвижности механизма игловодителя и нитепритягивателя швейной машины, число, класс и порядок присоединенных к исходному механизму структурных групп, записать формулу строения механизма и определить класс механизма (рис. 3)

1. Количество подвижных звеньев n = 5;

2. Составляем таблицу кинематических пар:

Обозначение кинематической пары

Звенья, образующие пару

4.Подвижность механизма по Формуле Чебышева

5.Раскладываем механизм на структурные группы, каждая из которых должна иметь нулевую подвижность (W = 0);

6.формула строения данного механизма имеет вид

Таким образом, механизм является механизмом второго класса, так как в его состав входят только группы второго класса.

Вопросы для самопроверки:

1. Приведите определения машины и механизма.

2. На какие виды делятся машины по своему функциональному назначению?

3. Назовите основные виды механизмов.

4. Какие механизмы называют рычажными?

5. Приведите определения звена, кинематической пары, кинематической цепи.

6. По какому признаку кинематические пары делятся на классы, высшие и низшие?

7. Каковы достоинства и недостатки высших и низших кинематических пар?

8. Объясните физический смысл числовых коэффициентов в структурных формулах

9. Почему большинство механизмов имеют одну степень свободы (подвижность равная единице)?

10. Можно ли в механизме с одной степенью свободы изменить положение звеньев, не меняя положение входного звена?

11. Сформулируйте принцип образования механизма

12. Приведите примеры структурных групп второго и третьего классов.

13Каким образом определяется порядок группы?

14. Что определяет класс механизма?

15. Для чего необходимо знать класс механизма?

16. Назовите передачи вращательного движения?

17. В чем состоит отличие гидравлических и пневматических механизмов от механизмов с твердыми звеньями?

2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ

2.1. Задачи и методы

Рычажные механизмы используются в качестве передаточных механизмов, воспроизводящих заданную функциональную зависимость между перемещениями входных и выходных звеньев. Они часто используются также и для перемещения некоторого объекта из одного положения в другое. Механизмы, в состав которых входят только вращательные пары, называются шарнирными. Если в шарнирном четырехзвенном механизме заменить одну или две вращательные пары на поступательные, то можно получить: кривошипно-ползунный механизм, кулисный, синусный, механизм эллипсографа.

Задачами кинематического анализа рычажных механизмов являются: определение положений звеньев механизма; траекторий отдельных точек звеньев механизма; скоростей и ускорений точек звеньев механизма; угловых скоростей и ускорений звеньев.

Для решения этих задач используются аналитические, графоаналитические, графические и экспериментальные методы исследования. Задача об аналитическом определении скоростей и ускорений решается дифференцированием по времени уравнений для определения положений звеньев, что приводит к системе линейных уравнений относительно искомых величин. Более просто, однако с меньшей точностью, задачи кинематического анализа решаются графическим способом. Положения звеньев механизма находятся с помощью простейших графических построений. Скорости и ускорения определяются с помощью кинематических диаграмм, полученных графическим дифференцированием диаграммы перемещения заданной точки звена.

Достаточно простым и вместе с тем достаточно точным и наглядным является графоаналитический метод (метод планов скоростей и ускорений). Он основан на графическом решении векторных уравнений, составленных для определения искомых скоростей и ускорений. Составление векторных уравнений связано с использованием уравнений двух типов: одного — связывающего скорости (ускорения) двух точек, принадлежащих одному звену, и второго — связывающего скорости (ускорения) двух точек, совпадающих в данный момент, но принадлежащих разным звеньям поступательной пары.

2.2. Графоаналитический метод

На практике широко применяют метод планов скоростей и ускорений. Метод основан на графическом решении векторных уравнений движения. Для построения планов скоростей и ускорений механизма должна быть известна его кинематическая схема и задан закон движения входного звена.

В качестве примера рассмотрим кинематику кривошипно-коромыслового механизма (механизма игловодителя швейной машины) (рис.4).

Для заданного положения механизма известны угловые скорости и ускорения входного звена. Для простоты решения задачи будем полагать, что угловое ускорение входного звена равно нулю.

Построение плана скоростей начинается с определения скорости точка А кривошипа

Вектор скорости VA направлен перпендикулярно кривошипу ОА в направлении его вращения (угловой скорости). Точка В, принадлежащая звену 2, рассматривается в относительном движении вокруг точки А. Скорость точки В можно представить как векторную сумму скоростей переносного и относительного движений. Переносным движением будем считать скорость точки А, а относительным – вращательное движение звена 2 вокруг точки А.Обозначая последнюю через VВА, получаем следующее уравнение для скорости точки В:

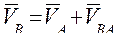, (5)

Структурный анализ плоского рычажного механизма

Структурная схема механизма

Рисунок 1.1 — Структурная схема механизма

Таблица 1 — Звенья механизма

Структурная схема механизма состоит из пяти подвижных звеньев и неподвижной стойки, представленной шарнирно-неподвижной опорой и двумя направляющими ползунов 3 и 5.

Подвижность механизма

Подвижность механизма определяем по формуле Чебышева:

где W — подвижность механизма;

n — число подвижных звеньев;

p₅ и p₄ — соответственно число пар пятого и четвертого класса.

Для определения значений p₄ и p₅ найдем все кинематические пары, входящие в состав рассматриваемой кинематической цепи. Результаты исследования заносим в таблицу 1.

Таблица 2 — Кинематические пары

Из анализа данных (таблица 2) следует, что исследуемая схема кривошипно-ползунного механизма представляет собой замкнутую кинематическую цепь и состоит из семи пар пятого класса, пар четвертого класса в составе структуры нет. Следовательно, p₅=7, а p₄=0.

Подставив найденные значения n, p₄ и p₅ в формулу (1), получим:

Полученный результат означает, что для однозначного описания положения всех звеньев механизма в рассматриваемой плоскости достаточно знать одну обобщенную координату ц₁.

Анализ состава структуры механизма

Для решения данной задачи используется структурная классификация механизмов, предложенная профессором Ассуром, согласно которой плоские рычажные механизмы состоят из структурных групп звеньев и первичных (элементарных) механизмов.

Начиная с выходных звеньев — ползунов 3 и 5, разбиваем рассматриваемую схему кривошипно-ползунного механизма на группы звеньев. При этом руководствуемся следующим правилом: если выделенная группа звеньев обладает совместно нулевой подвижностью, то эта группа звеньев является структурой группой Ассура (СГА).

Количество подвижных звеньев определяет класс СГА.

Поводок — это конечное звено СГА, входящее в состав кинематической пары и имеющее свободный элемент звена.

Количество поводков определяет порядок группы, а вид СГА определяется ее структурной схемой.

Рассмотрим группу звеньев 2-3 (рисунок 1.2).

Рисунок 1.2 — Группа звеньев 2-3

Данная группа состоит из двух подвижных звеньев: шатун 2 и ползун 3, и трех кинематических пар:

1-2 вращательная пара пятого класса;

2-3 вращательная пара пятого класса;

3-0 поступательная пара пятого класса.

Следовательно, структурная формула — ВВП, являющаяся вторым видом.

Поводки представлены звеном 1 и направляющей ползуна.

Подставив выявленные значения в формулу (1), получим:

Следовательно, группа звеньев 2-3 является структурной группой Ассура второго класса, второго порядка, второго вида.

Рассмотрим группу звеньев 4-5 (рисунок 1.3).

Рисунок 1.3 — Группа звеньев 4-5

Данная группа состоит из двух подвижных звеньев: шатун 4 и ползун 5, и трех кинематических пар:

1-4 вращательная пара пятого класса;

4-5 вращательная пара пятого класса;

5-0 поступательная пара пятого класса.

Следовательно, структурная формула — ВВП, являющаяся вторым видом.

Поводки представлены звеном 1 и направляющей ползуна.

Подставив выявленные значения в формулу (1), получим:

Следовательно, группа звеньев 4-5 является структурной группой Ассура второго класса, второго порядка, второго вида.

Рассмотрим группу звеньев 0-1 (рисунок 1.3).

Рисунок 1.3 — Группа звеньев 0-1

Данная группа состоит из подвижного звена кривошипа 1, стойки 0 и одной кинематической пары (вращательная 0-1)

Подставив найденные значения в формулу (1), получим:

Следовательно, группа звеньев 0-1 не является структурной группой Ассура, а представляет собой первичный механизм, подвижность которого равна единице, т.е. существует одна обобщенная координата.

Из проведенного анализа следует, что число степеней свободы механизма равно единице; механизм имеет следующий структурный состав (рисунок 1.4): первичный механизм с подвижностью равной единице и две структурные группы Ассура второго класса, второго порядка, второго вида.

Рисунок 1.4 — Структурный состав кривошипно-ползунного механизма

Вывод: подвижность механизма определяется подвижностью первичного механизма, входящего в его состав. Класс механизма определяется классом наиболее сложной структурной группы. Рассмотренный механизм является механизмом второго класса.