Расчет среднего удельного веса

Средние величины в статистике: сущность, свойства, виды. Примеры решения задач

Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности, ведь значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть и случайные.

Приведем примеры экономических показателей, основанных на вычислении средней величины и раскрывающих ее сущность:

• расчет средней заработной платы работников предприятия осуществляется делением общего фонда заработной платы на число работников;
• средний размер вклада в банке находят делением суммы вкладов в денежном выражении на количество вкладов;
• для определения средней дневной выработки одного работника необходимо объем работ (количество деталей), выполненных работником за определенный период разделить на число дней в этом периоде.

Виды средних величин, используемых в статистике

Рассмотрим основные виды средних величин, используемых при решении социально-эконмических и аналитических задач.

Средняя арифметическая простая вычисляется по формуле:

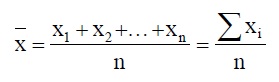
Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по не сгруппированным данным. Пример применения формулы средней арифметической простой представлен в задаче 1.

Средняя арифметическая взвешенная определяется по формуле:

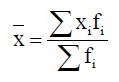
При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. Пример применения формулы средней арифметической взвешенной представлен в задаче 2.

Средняя гармоническая простая определяется по формуле:

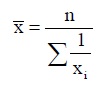
Средние гармонические используются тогда, когда по экономическому содержанию имеется информация для числителя, а для знаменателя ее необходимо предварительно определить.

Средняя гармоническая взвешенная определяется по формуле:

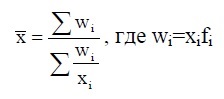
Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов. Пример применения формулы средней гармонической взвешенной представлен в задаче 3.

Средняя геометрическая простая (невзвешенная) опеределяется по формуле:

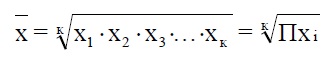
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.

Средняя квадратическая простая (невзвешенная) опеределяется по формуле:

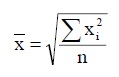
Средняя квадратическая лежит в основе вычислений ряда сводных расчетных показателей.

Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана. Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Пример определения медианы и моды для дискретного ряда чисел представлен в задаче 1.

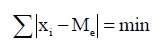
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.

Для интервального ряда расчет моды осуществляется по формуле:

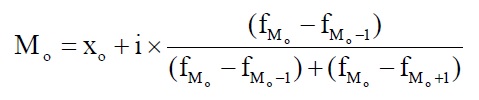
где Хо — нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); i — величина модального интервала; f Мо — частота модального интервала; f Мо-1 — частота интервала, предшествующего модальному; f Мо+1 — частота интервала, следующего за модальным.

Для интервального ряда расчет медианы осуществляется по формуле:

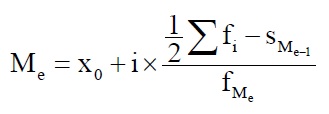
Хо — нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); i — величина медианного интервала; Sme-1 — накопленная частота интервала, предшествующего медианному; f Me — частота медианного интервала.

Примеры решения задач по теме «Средние величины в статистике»

Задача 1. Дан ряд чисел: 15; 15; 12; 14; 13. Найдите размах, среднее арифметическое, медиану и моду этого ряда.

Решение

1) Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел. В данном случае размах равен R = 15-12 = 3

2) Среднее арифметическое данного ряда находим по формуле средней арифметической простой. Хср = (15+15+12+14+13)/5=13,8

3) Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12; 13; 14; 15; 15.
Медиана нечетного количества чисел в дискретном ряде – это число, записанное посередине. Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Поскольку в нашем случае количество чисел ряда нечетноне, то Ме = 14.

4) Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других. Так как число 15 встречается в нашем ряде чаще других, то Мо = 15.

Задача 2. Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:

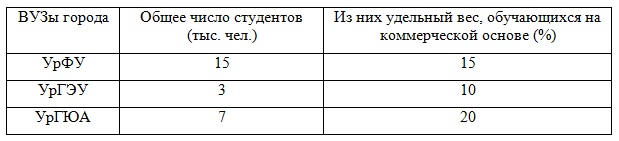
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов.

Решение

Для решения расширим предложенную таблицу:

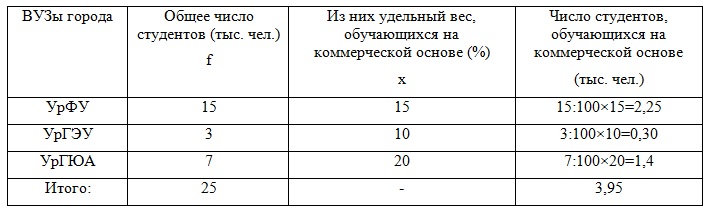
Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе определим по формуле средней арифметической взвешенной: Хср = (15×15+3×10+7×20) / (15+3+7) = 15,8%.

Ответ. Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе равен 15,8%, число этих студентов – 3 950 человек.

Задача 3. Сумма невыплаченной своевременно задолженности по кредитам на 1 июля составила 92,4 млн. денежных единиц. По отдельным отраслям экономики она распределялась следующим образом:

Определить средний процент невыплаченной своевременно задолженности. Обоснуйте выбор формы средней.

Решение

Поскольку на различных предприятиях сумма задолженности по кредитам разная при разных удельных весах, то применим формулу средней гармонической взвешенной.
Хср = ΣW / Σ(W/х) = (32+14+46,4)/(32/20+14/28+46,4/16) = 92,4/5 = 18,48 %.

Ответ. Средний процент невыплаченной своевременно задолженности равен 18,48%.

Другие статьи по данной теме:

• назад:Абсолютные и относительные величины в статистике. Примеры решения задач
• далее:Показатели вариации: понятие, виды, формулы для вычислений. Примеры решения задач

Список использованных источников

1. Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
2. Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики, информатики, финансов и права. — М., 2003;
3. Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
4. Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика» для студентов экономических специальностей: УрГЭУ, 2007;

Удельный вес

Среди множества параметров, характеризующих свойства материалов существует и такой как удельный вес. Иногда применяют термин плотность, но это не совсем верно. Но так или иначе эти оба термина имеют собственные определения и имеют хождение в математике, физике и множестве других наук, в том числе и материаловедении.

Определение удельного веса

Физическая величина, являющаяся отношением веса материала к занимаемому им объему, называется УВ материала.

Материаловедение ХХI века далеко ушло вперед в и уже освоены технологии, которые каких-то сто лет назад считались фантастикой. Эта наука может предложить современной промышленности сплавы, которые отличаются друг от друга качественными параметрами, но и физико-техническими свойствами.

Для определения того, как некий сплав может быть использован для производства целесообразно определить УВ. Все предметы, изготовленные с равным объемом, но для их производства был использованы разные виды металлов, будут иметь разную массу, она находится в четкой связи с объемом. То есть отношение объема к массе это есть некое постоянное число, характерная для этого сплава.

Для расчета плотности материала применяют специальную формулу, имеющую прямую связь с УВ материала.

Кстати, УВ чугуна, основного материала для создания стальных сплавов, можно определить весом 1 см 3 , отраженного в граммах. Тем больше УВ металла, тем тяжелее будет готовое изделие.

Формула удельного веса

Формулу расчета УВ выглядит как отношение веса к объему. Для подсчета УВ допустимо применять алгоритм расчета, который изложен в школьном курсе физики.
Для этого необходимо использовать закон Архимеда, точнее определение силы, которая является выталкивающей. То есть груз с некоей массой и при этом он держится на воде. Другими словами на него влияют две силы – гравитации и Архимеда.

Формула для расчета архимедовой силы выглядит следующим образом

F=g×V,

где g – это УВ жидкости. После подмены формула приобретает следующий вид F=y×V, отсюда получаем формулу УВ груза y=F/V.

Разница между весом и массой

В чем состоит разница между весом и массой. На самом деле в быту, она не играет ни какой роли. В самом деле, на кухне, мы не делаем развития между весом курицы и ее массой, но между тем между этими терминами существуют серьезные различия.

Эта разница хорошо видна при решении задач, связанных с перемещением тел в межзвездном пространстве и ни как имеющим отношения с нашей планете, и в этих условиях эти термины существенно различаются друг от друга.
Можно сказать следующее, термин вес имеет значение только в зоне действия силы тяжести, т.е. если некий объект находиться рядом с планетой, звездой и пр. Весом можно называть силу, с которой тело давит на препятствие между ним и источником притяжения. Эту силу измеряют в ньютонах. В качестве примера можно представить следующую картину — рядом с платным образованием находиться плита, с расположенным на ее поверхности неким предметом. Сила, с которой предмет давит на поверхность плиты и будет весом.

Масса тела напрямую связана с инерцией. Если детально рассматривать это понятие то можно сказать, что масса определяет размер гравитационного поля создаваемого телом. В действительности, это одна из ключевых характеристик мироздания. Ключевое различие между весом и массой заключается в следующем — масса не зависит от расстояния между объектом и источником гравитационной силы.

Для измерения массы применяют множество величин – килограмм, фунт и пр. Существует международная система СИ, в которой применяют привычные, нам килограммы, граммы и пр. Но кроме нее, в многих странах, например, Британских островах, существует собственная система мер и весов, где вес измеряют в фунтах.

Разница между удельным весом и плотностью

УВ – что это такое?

Удельный вес – это есть отношение веса материи к его объему. В международной системе измерений СИ его измеряют как ньютон на кубический метр. Для решения определенных задач в физике УВ определяют следующим образом – насколько обследуемое вещество тяжелее, чем вода при температуре 4 градусов при условии того, что вещество и вода имеют равные объемы.

По большей части такое определение применяют в геологических и биологических исследованиях. Иногда, УВ, рассчитываемый по такой методике, называют относительной плотностью.

В чем отличия

Как уже отмечалось, эти два термина часто путают, но так как, вес напрямую зависим от расстояния между объектом и гравитационным источником, а масса не зависит от этого, поэтому термины УВ и плотность различаются между собой.
Но необходимо принять во внимание то, что при некоторых условиях масса и вес могут совпадать. Измерить УВ в домашних условиях практически невозможно. Но даже на уровне школьной лаборатории такую операцию достаточно легко выполнить. Главное что бы лаборатория была оснащена весами с глубокими чашами.

Предмет необходимо взвесить при нормальных условиях. Полученное значение можно будет обозначить как Х1, после этого чашу с грузом помещают в воду. При этом в соответствии с законом Архимеда груз потеряет часть своего веса. При этом коромысло весов будет перекашиваться. Для достижения равновесия на другую чашу необходимо добавить груз. Его величину можно обозначить как Х2. В результате этих манипуляций будет получен УВ, который будет выражен как соотношение Х1 и Х2. Кроме вещества в твердом состоянии удельных можно измерить и для жидкостей, газов. При этом замеры можно выполнять в разных условиях, например, при повышенной температуре окружающей среды или пониженной температуры. Для получения искомых данных применяют такие приборы как пикнометр или ареометр.

Единицы измерения удельного веса

В мире применяют несколько систем мер и весов, в частности, в системе СИ УВ измеряют в отношении Н (Ньютон) к метру кубическому. В других системах, например, СГС у удельного веса используется такая единица измерения д(дин) к сантиметру кубическому.

Металлы с наибольшим и наименьшим удельным весом

Кроме того, что понятие удельного веса, применяемое в математике и физике, существуют и довольно интересные факты, например, об удельных весах металлов из таблицы Менделеева. если говорить о цветных металлах, то к самым «тяжелым» можно отнести золото и платину.

Эти материалы превышают по удельному весу, такие металлы как серебро, свинец и многие другие. К «легким» материалам относят магний с весом ниже чем у ванадия. Нельзя забывать и радиоактивных материалах, к примеру, вес урана составляет 19,05 грамм на кубический см. То есть, 1 кубический метр весит 19 тонн.

Удельный вес других материалов

Наш мир сложно представить без множества материалов, используемых в производстве и быту. Например, без железа и его соединений (стальных сплавов). УВ этих материалов колеблется в диапазоне одной – двух единиц и это не самые высокие результаты. Алюминий, к примеру, обладает низкой плотностью и малым удельным весом. Эти показатели позволили его использовать в авиационной и космической отраслях.

Удельный вес металлов

Медь и ее сплавы, обладают удельным весом сопоставимый со свинцом. А вот ее соединения – латунь, бронза легче других материалов, за счет того, в них использованы вещества с меньшим удельным весом.

Как рассчитать удельный вес металлов

Как определить УВ — этот вопрос часто встает у специалистов занятых в тяжелой промышленности. Эта процедура необходима для того, что бы определить именно те материалы, которые будет отличаться друг от друга улучшенными характеристиками.

Одна из ключевых особенностей металлических сплавов заключается в том, какой металл является основой сплава. То есть железо, магний или латунь, имеющие один объем будут иметь разную массу.

Плотность материала, которая рассчитывается на основании заданной формулы имеет прямое отношение к рассматриваемому вопросу. Как уже отмечено, УВ – это соотношение веса тела к его объему, надо помнить, что эта величина может быть определена как силу тяжести и объема определенного вещества.

Для металлов УВ и плотность определяют в той же пропорции. Допустимо использовать еще одну формулу, которая позволяет рассчитать УВ. Она выглядит следующим так УВ (плотность) равна отношению веса и массы с учетом g, постоянной величины. Можно сказать, что УВ металла может, носит название веса единицы объема. Дабы определить УВ необходимо массу сухого материала поделить на его объем. По факту, эта формула может быть использована для получения веса металла.

Кстати, понятие удельного веса широко применяют при создании металлических калькуляторов, применяемых для расчета параметров металлического проката разного типа и назначения.

УВ металлов измеряют в условиях квалифицированных лабораторий. В практическом виде этот термин редко применяют. Значительно чаще, применяют понятие легкие и тяжелые металлы, к легким относят металлы с малым удельным весом, соответственно к тяжелым относят металлы с большим удельным весом.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Средняя арифметическая взвешенная

Когда исходные данные сгруппированы, то расчёт средней производится по

формуле средней арифметической взвешенной:

Где f_i – частота ряда распределения, с которой отдельные варианты встречаются в совокупности (или удельный вес отдельных значений во всей совокупности).

Например: Рабочие бригады по возрасту распределились следующим образом:

Средний возраст рабочего бригады составляет

Если исходная информация представлена в виде интервального ряда распределения, то средняя арифметическая взвешенная определяется по формуле:

Где X_c — центральное (серединное) значение признака в интервале.

Например: По имеющимся данным определить средний стаж рабочего бригады:

Для расчёта средней арифметической взвешенной интервального ряда распределения определим центральное (серединное) значение признака в каждом интервале. Среднее значение интервала находится как полусумма нижней границы данного интервала и нижней границы следующего интервала:

Оформим исходные данные а следующем виде:

Средний стаж рабочего бригады составляет

Если в интервальном ряду распределения имеются «открытые» интервалы, то для установления центральных (серединных) значений «открытых» интервалов на каждый из них условно распространяется величина смежного «закрытого» интервала.

Например: Работники организации по величине заработной платы за январь 2013 года распределились следующим образом:

Определить по имеющимся данным среднюю зарплату работников организации.

Для расчёта средней арифметической взвешенной интервального ряда распределения определим центральное (серединное) значение признака в каждом интервале. На каждый открытый интервал условно распространим величину смежного закрытого интервала:

Частоты при расчете средних арифметических могут быть выражены не только абсолютными величинами, но и относительными величинами – частостями. Результаты применительно к одинаковым вариантам будут совпадать. В данном примере численность работников выражена не частотами, а частостями – удельными весами численности отдельных групп во всей совокупности, что не влияет на порядок расчёта средней.

Средняя зарплата работников организации за январь 2013 года составляет:

Необходимо небольшое пояснение применительно к расчету средней в интервальных рядах распределения. В действительности распределение отдельных вариантов в пределах интервала может оказаться неравномерным. В этом случае середина интервала будет в той или иной степени отличаться от фактической средней по интервалу. Это в свою очередь может повлиять на правильность общей средней, исчисленной по данным интервального ряда. Степень расхождения зависит от ряда причин. Во-первых, от числа вариант, чем больше число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Во-вторых, от величины интервала. Если интервал невелик, то ошибка будет незначительной, т.к. групповая средняя будет мало отличаться от середины интервала. В-третьих, от характера распределения. Чем симметричнее распределение, тем ошибка меньше. В-четвертых, размер ошибки зависит от принципа построения интервального ряда. При равных интервалах середина интервала будет ближе к средней по данной группе. При наличии открытых интервалов расхождение, как правило, взрастает из-за условного обозначения неизвестных границ. Общая средняя равна средней из частных (групповых) средних, взвешенных по численности соответствующих частей совокупности. Это правило имеет большое значение для всей статистики – организации сбора и обработки данных, их анализа.

Свойства средней арифметической:

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты. Другими словами, постоянный множитель может быть вынесен за знак средней.

2. Если от каждой варианты отнять (прибавить) какое-либо произвольное число, то новая средняя уменьшится (увеличится) на то же число:

3. Если каждую варианту умножить (разделить) на какое-то произвольное число, то средняя арифметическая увеличится (уменьшится) во столько раз

4. Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится. Дело в том, что веса при исчислении средней арифметической выполняют роль удельного веса (соотношений между группами по количеству единиц). Поэтому замена частот частостями не меняет значения средней.

5. Сумма отклонений отдельных вариантов от средней арифметической всегда равняется нулю.

Перечисленные свойства могут быть использованы для того, чтобы облегчить технику исчисления средней арифметической.

Например. Можно из всех значений признака вычесть произвольную постоянную величину (лучше значение серединной варианты или варианты с наибольшей частотой), полученные разности сократить на общий множитель (лучше на величину интервала), а частоты выразить частостями (в процентах) и исчисленную среднюю умножить на общий множитель и прибавить произвольную постоянную величину. Иногда этот способ расчета средней арифметической также называется способом расчета от условного нуля. Широкое применение для обработки статистических материалов современных ЭВМ сужает необходимость исчисления средних по упрощенным схемам.

Как рассчитать удельный вес в процентах

• Как рассчитать удельный вес в процентах
• Как вычислить процентное содержание
• Как найти стоимость валовой продукции

Формула и алгоритм расчёта удельного веса в процентах

Есть совокупность (целое), в состав которой входит несколько компонентов (составных частей).

Введём следующие обозначения:

X1, X2, X3, . Xn — части целого.

Они могут быть выражены в различных единицах измерения — рублях, штуках, килограммах и т.п.

Чтобы найти удельный вес каждой части совокупности (Wi) нужно воспользоваться следующей формулой:

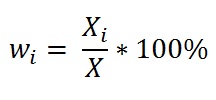
То есть значение каждой части делится на общую сумму и умножается на 100 процентов.

Удельный вес будет показывать ценность, значимость или влияние каждого элемента совокупности.

Для проверки правильности расчётов нужно сложить все удельные веса между собой — их сумма должна быть равна 100 процентам.

Пример расчёта удельного веса в процентах

Компания в отчётном периоде выпустила 100000 тетрадей.

• тетради 12 листов — 30000 штук.
• тетради 18 листов — 10000 штук.
• тетради 24 листа — 10000 штук.
• тетради 48 листов — 30000 штук.
• тетради 96 листов — 20000 штук.

Требуется найти удельный вес каждого вида продукции.

Для решения данной задачи воспользуемся формулой, которая была приведена выше.

1) W1 (тетради 12 листов) = (30000 / 100000) * 100% = 0,3 * 100% = 30%.

2) W1 (тетради 18 листов) = (10000 / 100000) * 100% = 0,1 * 100% = 10%.

3) W1 (тетради 24 листа) = (10000 / 100000) * 100% = 0,1 * 100% = 10%.

4) W1 (тетради 48 листов) = (30000 / 100000) * 100% = 0,3 * 100% = 30%.

5) W1 (тетради 96 листов) = (20000 / 100000) * 100% = 0,2 * 100% = 20%.

Суммируем полученные удельные веса:

30% + 10% + 10% + 30% + 20% = 100%.

Это означает, что всё было посчитано правильно.

Расчёт удельного веса в программе Эксель (Excel)

Если совокупность включает в себя довольно большое число элементов, то удельный вес каждого элемента очень удобно рассчитывать с помощью программы Excel.

Вот как это можно сделать (на примере задачи про тетради):

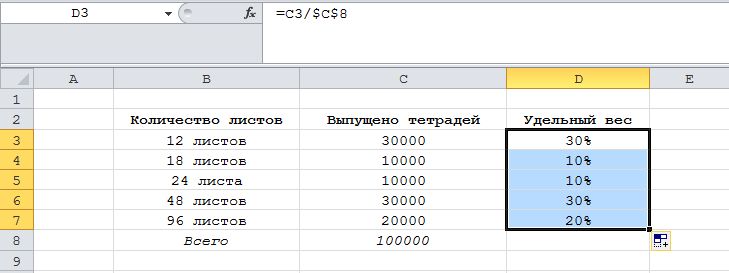
1) Составляем таблицу, состоящую из 3 столбцов: 1 столбец — название, 2 столбец — значение, 3 столбец — удельный вес.

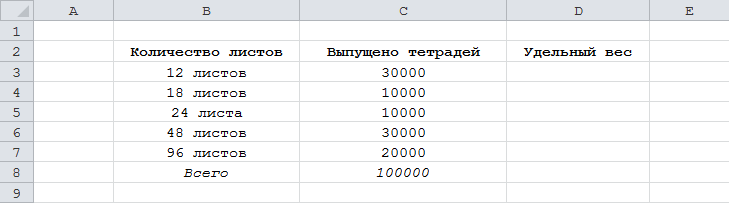
2) В ячейку D3 записываем формулу для удельного веса тетрадей 12 листов:

Ссылка на ячейку C8 является абсолютной, так как она будет фигурировать во всех формулах.

Устанавливаем процентный формат ячейки — для этого нажимаем на кнопку «%», расположенную на панели инструментов.

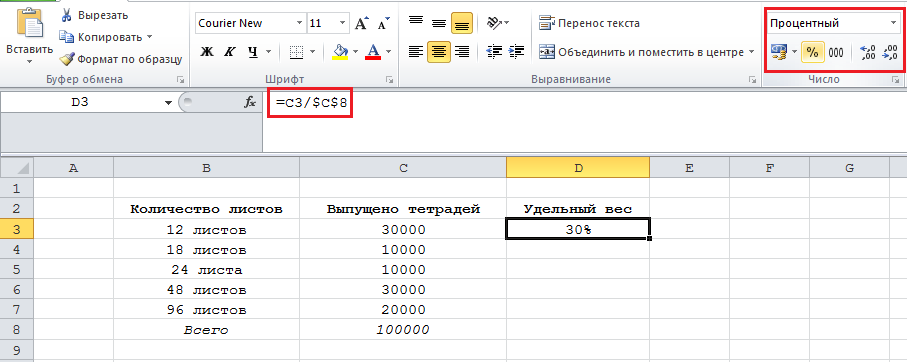
3) Для расчёта остальных удельных весов копируем формулу из ячейки D3 в нижестоящие ячейки (D4, D5 и т.д.).

При этом процентный формат будет применён к данным ячейкам автоматически, и его не нужно будет устанавливать.

При нахождении удельного веса в процентах в Excel очень полезной может оказаться кнопка «Увеличить разрядность», она расположена на панели инструментов рядом с кнопкой процентного формата:

Эта кнопка понадобится в том случае, когда удельный вес представляет собой дробь, и нужно отображать десятые и сотые доли.

4) Последний шаг — складываем удельные веса с помощью функции СУММ.

Расчет среднего удельного веса

Чтобы понять, как рассчитать удельный вес, надо знать, что это словосочетание используется в трёх случаях. Первый — это название физической величины, определённого размера. Размерность позволяет сравнивать между собой однородные значения разных объектов. Для характеристики введены специальные, присущие этой величине, единицы измерения. Второй — доля чего-то в общей массе. Третий — относительная плотность.

Формулы для естественно-научных расчётов

Если говорить об удельном весе (γ), как физической величине, то его можно рассчитать по формулам. В физических расчётах его принято обозначать — γ (гамма). Если известны вес тела (P) и его объём (V), то искомое значение — это отношение первого ко второму (P/V). Из курса физики известно, что вес объекта — это масса (m), умноженная на ускорение свободного падения (g). Подставим эти величины для расчёта удельного веса в формулу γ=P/V. Получим γ=mg/V. По международным стандартам единицей его измерения является Ньютон на метр кубический (Н/м 3 ).

Из формулы понятно, что m/V — плотность (ρ). Таким образом, получается γ=ρg, то есть плотность, умноженная на ускорение. Плотности большинства веществ вычислены и систематизированы. Если использовать справочные таблицы, то вопрос о том, как посчитать удельный вес, легко решается. Однако так обстоит дело только в том случае, если погрешностью величины ускорения (g) можно пренебречь.

Сила тяжести для вычислений

Необходимо знать, что сила тяжести в разных точках нашей планеты немного отличается. Её величина изменяется в зависимости от географической широты. При этом минимальное составляет 9,780 м/с 2 . Максимальное достигает 9,832 м/с 2 . Среднее значение равно 9,80665м/с 2 . Перед тем, как рассчитать удельный вес, определяют этот показатель. В зависимости от точности, при расчётах выбирают разные цифры: 10,0 м/с 2 , 9,8 м/с 2 или 9,81 м/с 2 .

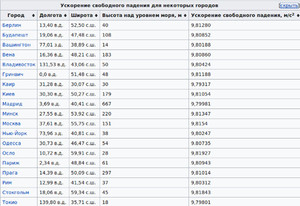
Необходимо также учитывать высоту предмета над уровнем моря и некоторые другие детали. У поверхности Земли силу тяжести измеряют гравиметрами. На других астрономических объектах рассчитывают, производя наблюдения за орбитами различных небесных тел и их вращением. Методом наблюдения и расчётов вычислена сила тяжести многих космических объектов.

Вот некоторые данные:

• на Юпитере —23,95 м/с 2 ;
• на Нептуне —11,09 м/с 2 ;
• на Сатурне —10,44 м/с 2 ;
• на Венере —8,88 м/с 2 ;
• на Уране —8,86 м/с 2 ;
• на Марсе —3,86 м/с 2 ;
• на Меркурии —3,7 м/с 2 ;
• на Луне —1,62 м/с 2 .

Итак, сила тяжести, действующая на тело, отличается в разных астрофизических условиях, а плотность объекта — величина постоянная и известная. Можно найти γ=ρg практически в любой точке. В невесомости, где отсутствует сила тяжести, это значение — ноль.

Относительная плотность продукции

Другим значением выражения удельный вес является относительная плотность. Это значение показывает во сколько раз вещество тяжелее или легче дистиллированной воды (при одинаковом объёме).

Вода здесь является эталоном. При этом температура её должна быть 4 градуса Цельсия. При этой температуре её плотность максимальна и составляет 999,973 кг/м 3 . Так как сравниваются величины, имеющие одинаковую размерность, результатом будет безразмерное число.

Пикнометр — это прибор для нахождения этого значения. Процедура определения простая. Сначала в чашу прибора наливают эталонную жидкость (воду). Производят взвешивание. Затем процесс повторяют уже с исследуемой субстанцией. При этом полученную величину умножают на абсолютную плотность (999,973 кг/м 3 ).

С помощью таких измерений в производстве косметической продукции проверяют консистенцию товаров (кремов, лосьонов). Используют их в пищевой промышленности и некоторых других производствах.

Для экономического и хозяйственного анализа

Это понятие часто используется при анализе хозяйственной и финансовой деятельности. А также в случаях, если требуется исследование структуры социальных и подобных им объектов.

При этом, чтобы понять, как считается удельный вес той или иной составляющей, надо знать, что имеется в виду. В широком смысле — это отношение части к общему количеству. Показатель может быть посчитан в долях или процентах.

Показатель экономической деятельности

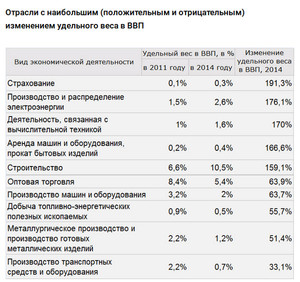
Для экономики государства обычно вычисляется доля от ВВП в процентах. Например, какую часть составляет та или иная отрасль промышленности от общего ВВП.

Например, удельный вес добавленной стоимости за год составил:

• В строительстве 10,5%.
• В сельском хозяйстве 7,0%.
• В розничной торговле 6,1%.
• В оптовой торговле 5,4%.

Нам важно знать, как получили эти цифры. Внутренний валовый продукт (ВВП) — это стоимость всех произведённых товаров и услуг в денежном выражении. Для вычислений требуется знать добавленную стоимость в отрасли. Если разделить её значение на общий ВВП и умножить на 100%, получим искомое число. При некоторых расчётах определяют не процент от общего, а долю. В этом случае на 100% умножать не требуется.

по дисциплине: «Статистика»

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

ЗАДАЧА 1. Для выявления зависимости между возрастом и числом членов семьи произвести группировку рабочих с порядковыми номерами с 1 по 15 включительно, приведенными в таблице 1. Результаты группировки изложить в табличной форме и сделать выводы.

Выборочные данные обследования рабочих завода

Как рассчитать удельный вес в различных областях?

Понятие удельного веса очень часто встречается в различных областях науки и жизни. Что же оно означает и как рассчитать удельный вес?

Понятие в физике

Удельный вес в физике определяется как вес вещества в единице объема. В системе измерений СИ эту величину измеряют в Н/м3. Чтобы понимать, сколько это 1 Н/м3, его можно сравнить с величиной в 0,102 кгс/м3.

Чтобы знать, как рассчитать у. в., нужно понимать формулу расчета. Формула имеет следующий вид:

где Р — вес тела в Ньютонах; V— объем тела в кубических метрах.

Если рассматривать для примера простую воду, то можно заметить, что ее плотность и удельный вес почти не отличаются и очень незначительно меняются с изменением давления или температуры. Ее у. в. равен 1020 кгс/м3. Чем больше в составе этой воды будет растворено солей, тем больше величина у. в. Этот показатель для морской воды гораздо больше, чем для пресной, и равен 1150 – 1300 кгс/м3.

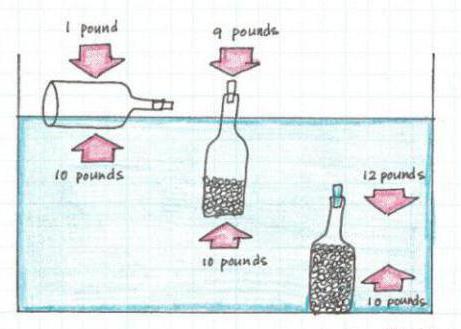
Ученый Архимед когда-то давным-давно заметил, что на погруженное в воду тело действует выталкивающая сила. Равна эта сила количеству жидкости, которую тело вытеснило. Когда тело весит меньше объема вытесненной жидкости, то оно плавает на поверхности и идет ко дну, если ситуация обратная.

Расчет удельного веса

«Как рассчитать удельный вес металлов?» — такой вопрос часто занимает тех, кто развивает тяжелую промышленность. Нужна эта процедура для того, чтобы среди различных вариаций металлов найти те, которые будут отличаться более качественными характеристиками.

Особенности различных сплавов заключаются в следующем: в зависимости от того, какой металл используют, будь то железо, алюминий или латунь, одного объема, в сплаве будут иметь различную массу. Плотность вещества, рассчитываемая по определенной формуле, имеет самое прямое отношение к вопросу, который задают рабочие, обрабатывая металлы: «Как расчитать удельный вес?».

Как уже упоминалось выше, у. в. есть отношением веса тела к его объему. Не стоит забывать, что эту величину еще определяют как силу тяжести взятого за основу объема определяемого вещества. Для металлов их у. в. и плотность находятся в том же соотношении, что и вес к массе испытуемого. Тогда можно использовать еще одну формулу, которая ответит на вопрос о том, как рассчитать удельный вес: у.в./плотность = вес/масса=g, где g — величина постоянная. Единицей измерения у. в. металлов также является Н/м3.

Таким образом, мы пришли к тому, что удельный вес металла носит название вес единицы объема плотного или непористого материала. Чтобы определить у. в., нужно массу сухого материала разделить на его объем в абсолютно плотном состоянии – по факту это формула, используемая для определения веса металла. Чтобы добиться такого результата, металл приводят в такое состояние, чтоб в его частицах не оставалось пор, и он имел однородную структуру.

Удельный вес в экономике

Удельный вес в экономике — один из самых часто обсуждаемых показателей. Рассчитывают его для анализа экономической, финансовой части хозяйственной деятельности организации и т.д. Это один из основных способов статистического анализа, а точнее, относительная величина этой структуры.

Зачастую понятие удельного веса в экономике – это обозначение какой-либо доли от общего объема. Единицей измерения в этом случае служит процентный показатель.

Как рассчитать удельный вес для экономической картины происходящего? Давайте рассмотрим:

У. в. = (Часть целого/Целое)Х100%.

Как видно, это всем известная формула нахождения процентного соотношения между целым и его частью. Это ведет за собой соблюдение 2 очень важных правил:

1. Общая структура рассматриваемого явления должна в общей сложности быть не более и не менее 100%.
2. Абсолютно не имеет значения, какую конкретно структуру рассматривают, будь то структура активов или удельный вес персонала, структура населения или доля затрат, расчет в любом случае будет проводиться по приведенной выше формуле.

Удельный вес в медицине

Удельный вес в медицине – понятие достаточно часто встречаемое. Используют его при проведении анализов. Давно известно, что у.в. воды пропорционален концентрации в ней растворенных веществ, чем их будет больше, тем больше будет удельный вес. У.в. дистиллированной воды при 4 градусах по Цельсию равен 1,000. Отсюда следует, что у.в. мочи может дать представление о количестве растворенных в ней веществ. Отсюда же можно сделать тот или иной диагноз.