Расчет прямозубой шестерни онлайн

Модуль зубьев зубчатого колеса

Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

Скачать ГОСТ 9563-60

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

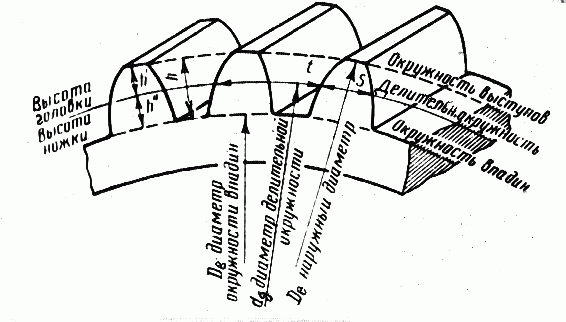
Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

где h — высота зубца.

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Расчет параметров колеса и шестерни косозубой передачи

Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Быстрое моделирование шестерней по параметрам

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых постах.

Отписаться от уведомлений вы всегда сможете в профиле автора.

Вопрос о моделировании шестерней поднимался неоднократно, но решения либо подразумевали использование серьезных платных программ, либо были слишком упрощенными и им не хватало инженерной строгости.

В этой статье я постараюсь с одной стороны, дать сухую мэйкерскую инструкцию, как смоделировать шестерню по нескольким легко измеряемым параметрам, с другой, не обойду и теорию.

В качестве примера возьмем шестерню от дроссельной заслонки автомобиля:

Это классическая цилиндрическая прямозубая шестерня с эвольвентным зацеплением (точнее, это две таких шестерни).

Принцип эвольвентного зацепления:

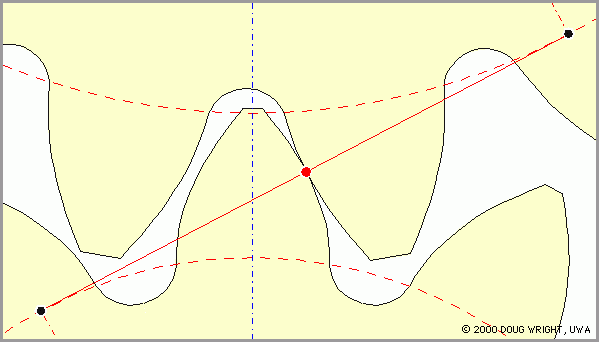
Для нас важно, что подавляющее большинство встречающихся в быту шестерней имеют именно эвольвентное зацепление.

Для изучения параметров шестерней воспользуемся программой с остроумным названием Gearotic. Мощнейшая узкоспециализированная программа для моделирования и анимирования всевозможных шестерней и передач.

Бесплатная версия не дает экспортировать сгенерированные шестерни, но нам и не надо. Непосредственно моделировать будем позже.

Итак, запускаем Gearotic

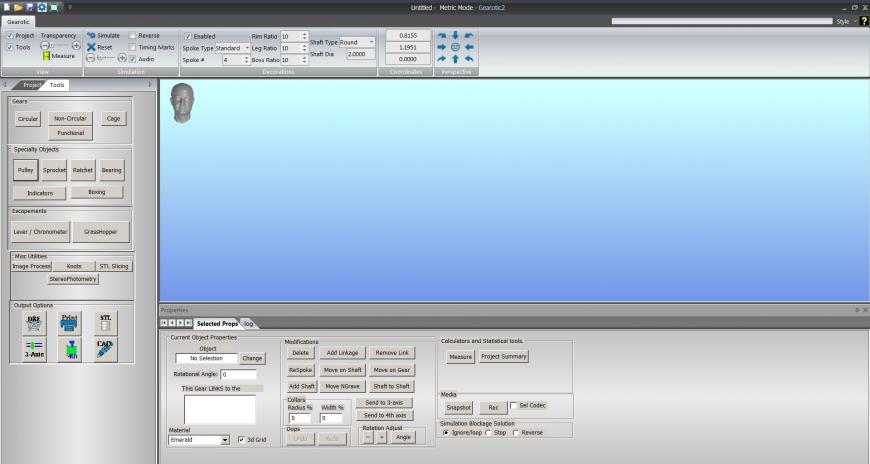
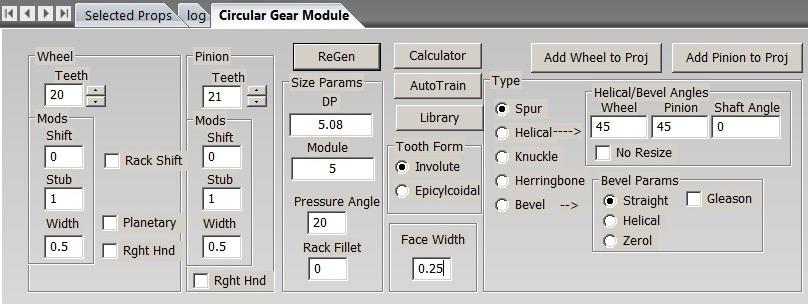
Первые два столбца Wheel и Pinion

Wheel — это будет наша шестерня, а Pinion — ответная часть, которая нас в данном случае не интересует.

Teeth — количество зубьев

Mods — модификаторы формы зуба. Самый простой способ понять, что они делают — поварьировать их. Не все параметры применяются автоматически. После изменения нужно нажимать кнопку ReGen. В нашем случае (как и в большинстве других) оставляем эти значения по умолчанию.

Галка Planetary — выворачивает шестерню зубьями внутрь (коронная шестерня).

Галка Rght Hnd (Right Hand) — меняет направление скоса у косозубых шестерней.

Блок Size Params

DP (Diametral Pitch) — число зубьев, деленное на диаметр делительной окружности (pitch diameter)

Неинтересный для нас параметр, т.к. измерять диаметр делительной окружности неудобно.

Module (модуль) — важнейший для нас параметр. Вычисляется по формуле M=D/(n+2), где D — внешний диаметр шестерни (легко измеряемый штангенциркулем), n — число зубьев.

Pressure Angle (угол профиля) — острый угол между касательной к профилю в данной точке и радиусом — вектором, проведенным в данную точку из центра колеса.

Существуют типичные значения этого угла: 14.5 и 20 градусов. 14.5 используется гораздо реже и в основном на очень маленьких шестернях, которые на FDM-принтере всё равно отпечатаются с большой погрешностью, так что на практике можно смело ставить 20 градусов.

Rack Fillet — сглаживание основания зуба. Оставляем 0.

Блок Tooth Form

Оставляем Involute — эвольвентное зацепление. Epicylcoidal — циклоидное зацепление, используемое в точном приборостроении, например, в часовых механизмах.

Face Width — толщина шестерни.

Spur — наша прямозубая шестерня.

Helical — косозубая шестерня:

Вернемся к нашей шестерне.

Большое колесо имеет 47 зубьев, внешний диаметр 44.6 мм, диаметр отверстия 5 мм, толщину 6 мм.

Модуль будет равен 44.6(47+2)=0.91 (округлим до второго знака).

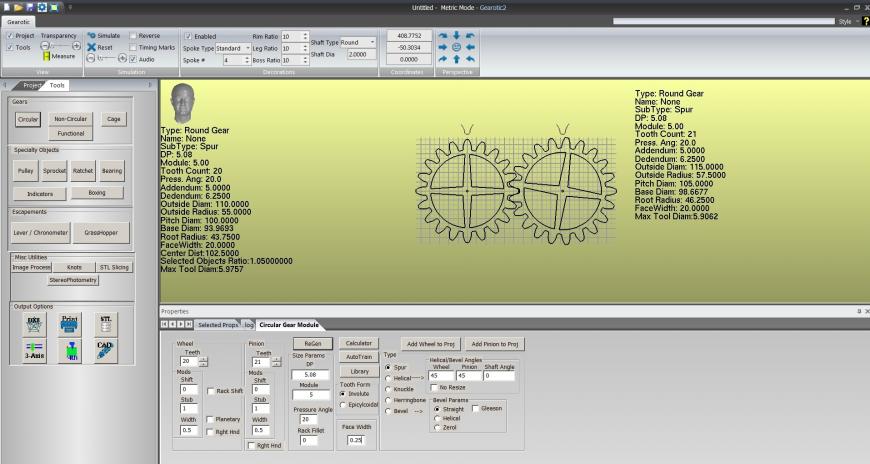
Вносим эти данные:

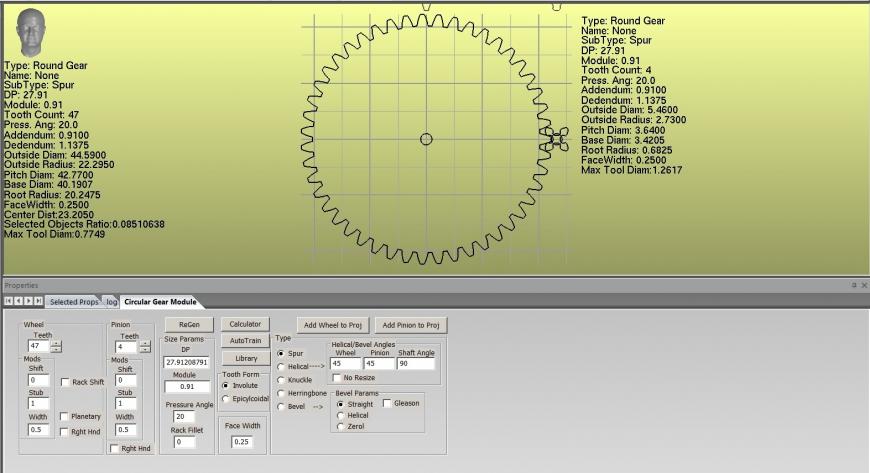
Слева расположена таблица параметров. Смотрим Outside Diam (внешний диаметр) 44.59 мм. Т.е. вполне в пределах погрешности измерения штангенциркуля.

Таким образом мы получили профиль нашей шестерни, выполнив всего одно простое измерение и посчитав количество зубьев.

Укажем толщину (Face Width) и диаметр отверстия (Shaft Dia в верхней части экрана). Жмем Add Wheel to Proj для получения 3d-визуализации:

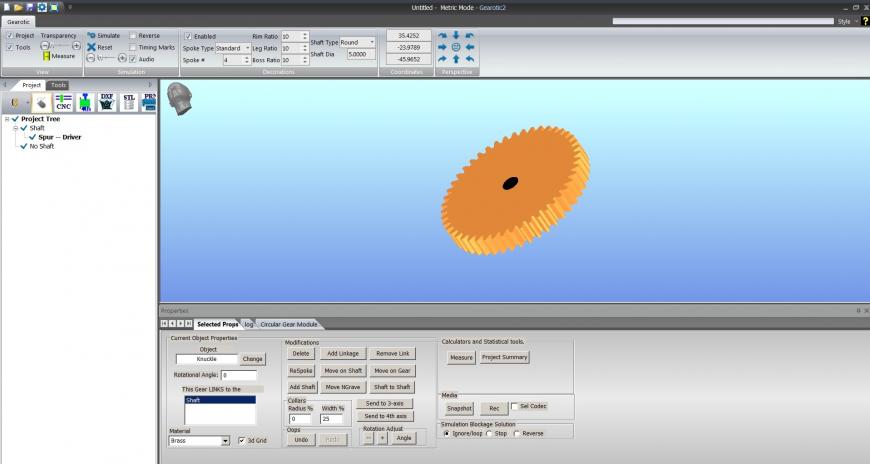
Увы, бесплатная версия не дает экспортировать результат, поэтому придется задействовать другие инструменты.

Устанавливаем FreeCAD Кто не владеет Фрикадом — не волнуйтесь, глубоких знаний не потребуется. Скачиваем плагин FCGear.

Находим папку, куда установился Фрикад. В папке Mod создаем папку gear и помещаем в нее содержимое архива.

После запуска Фрикад в выпадающем списке должен появиться пункт gear:

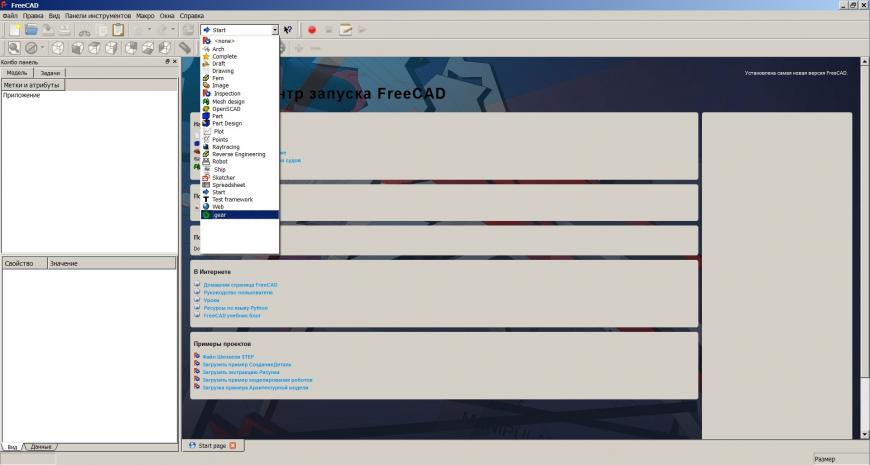
Выбираем его, затем Файл — Создать

Нажимаем на иконку involute gear вверху экрана, затем выделяем появившуюся шестерню в дереве слева и переходим на вкладку ‘Данные’ в самом низу:

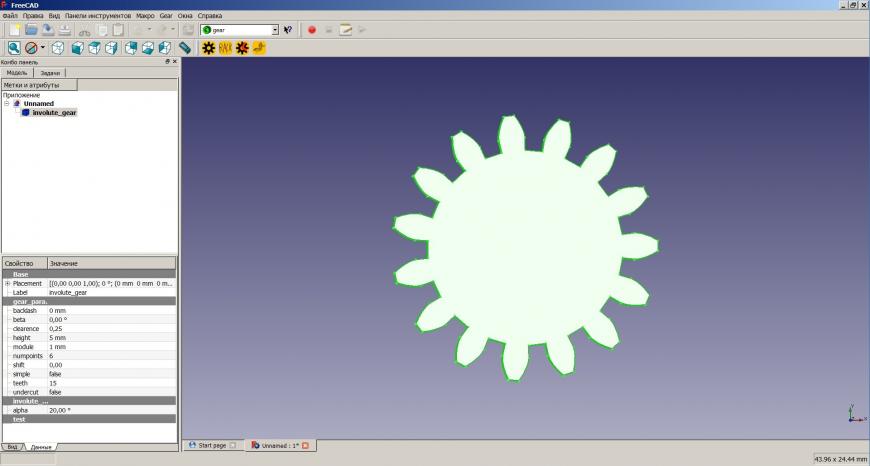
В этой таблице параметров

teeth — количество зубьев

height — толщина (или высота)

alpha — угол профиля

backlash — значение угла для косозубых шестерней (мы оставляем 0)

Остальные параметры являются модификаторами и, как правило, не используются.

Вносим наши значения:

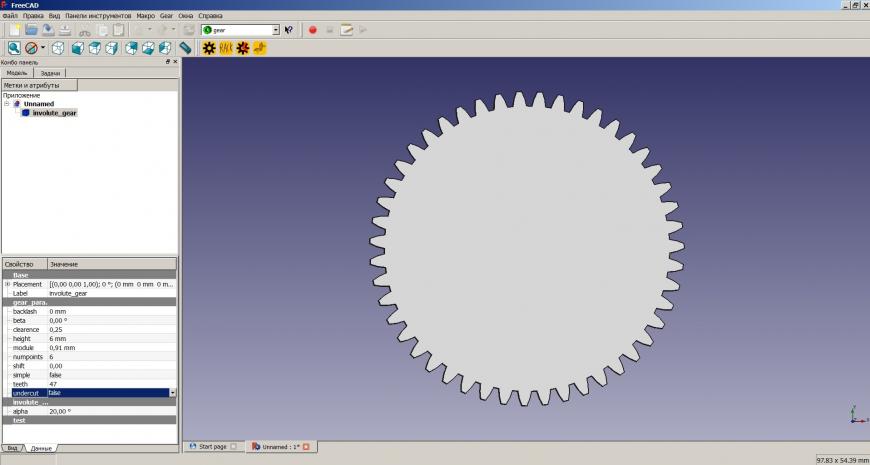
Добавим еще одну шестерню.

Укажем высоту 18 мм (общая высота нашей исходной шестерни), количество зубьев — 10, модуль 1.2083 (диаметр 14.5 мм)

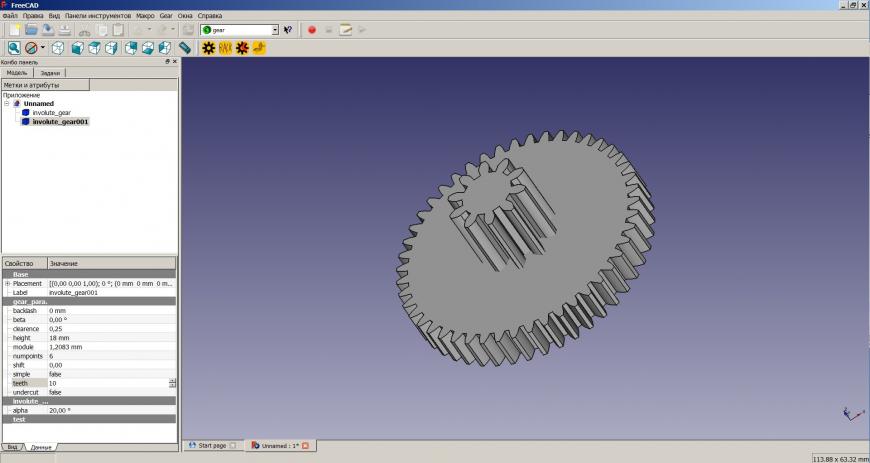
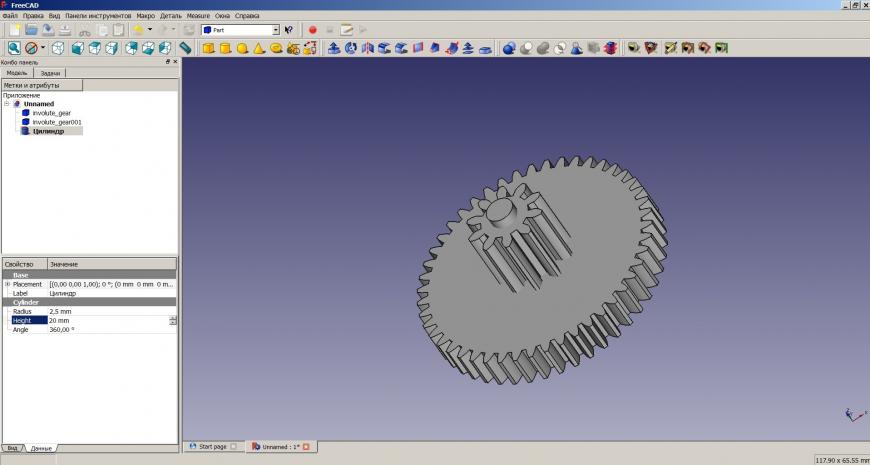
Удерживая клавишу Ctrl выделим в дереве шестерни и нажмем Создать объединение нескольких фигур на панели инструментов.

Затем, опять же удерживая Ctrl, выделим сначала получившуюся единую шестерню, а затем цилиндр и нажмем Выполнить обрезку двух фигур

Далее выделяем результат, Файл — Экспортировать. сохраняем в stl. Шестерня готова.

P.S. Хотел еще немного поговорить об экзотических случаях, но статья получилась большой, так что наверное, в другой раз.

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых постах.

Отписаться от уведомлений вы всегда сможете в профиле автора.

Подбор сменных зубчатых колес. Программа для подбора

Программа для подбора сменных зубчатых колес

ПОРЯДОК ПОЛЬЗОВАНИЯ ТАБЛИЦАМИ / ПРОГРАММОЙ

Для подбора сменных колес искомое передаточное отношение выражается в виде десятичной дроби с числом знаков соответственно требуемой точности. В «Основных таблицах» для подбора зубчатых колес (стр. 16—400) находим колонку с заголовком, содержащим первые три цифры передаточного отношения; по остальным цифрам находим строку, на которой указаны числа зубьев ведущих и ведомых колес.

Требуется подобрать сменные колеса гитары для передаточного отношения 0,2475586. Сначала находим колонку с заголовком 0,247—0000, а под ним ближайшее значение к последующим десятичным знакам искомого передаточного отношения (5586). В таблице находим число 5595, соответствующее набору сменных колес (23*43) : (47*85). Окончательно получаем:

i = (23*43)/(47*85) = 0,2475595. (1)

Относительная погрешность сравнительно с заданным передаточным отношением :

δ = (0,2475595 — 0,2475586) : 0,247 = 0,0000037.

Строго подчеркиваем: во избежание влияния возможной опечатки нужно обязательно проверить полученное соотношение (1) на калькуляторе. В тех случаях, когда передаточное отношение больше единицы, необходимо выразить его обратную величину в виде десятичной дроби, по найденному значению в таблицах отыскать числа зубьев ведущих и ведомых сменных колес и поменять ведущие и ведомые колеса местами.

Требуется подобрать сменные колеса гитары для передаточного отношения i = 1,602225. Находим обратную величину 1:i = 0,6241327. В таблицах для ближайшего значения 0,6241218 находим набор сменных колес: (41*65) : (61*70). Учитывая, что решение найдено для обратной величины передаточного отношения, меняем местами ведущие и ведомые колеса:

i = (61*70)/(41*65) = 1,602251

Относительная погрешность подбора

δ = (1,602251 — 1,602225) : 1,602 = 0,000016.

Обычно требуется подбирать колеса для передаточных отношений, выраженных с точностью до шестого, пятого, а в отдельных случаях и до четвертого десятичного знака. Тогда семизначные числа, приведенные в таблицах, можно округлять с точностью до соответствующего десятичного знака. Если имеющийся комплект колес отличается от нормального (см. стр. 15), то, например, при настройке цепей дифференциала или обкатки можно выбрать подходящую комбинацию из ряда соседних значений с погрешностью, удовлетворяющей условиям, изложенным на стр. 7—9. При этом некоторые числа зубьев можно заменять. Так, если число зубьев комплекта не свыше 80, то

(58*65)/(59*95) = (58*13)/(59*19) = (58*52)/(59*76)

«пятковую» комбинацию предварительно преобразуют так:

а затем, по полученным множителям подбирают числа зубьев.

ОПРЕДЕЛЕНИЕ ДОПУСТИМОЙ ПОГРЕШНОСТИ НАСТРОЙКИ

Очень важно различать абсолютную и относительную погрешности настройки. Абсолютной погрешностью называют разность между полученным и требуемым передаточными отношениями. Например, требуется иметь передаточное число i = 0,62546, а получено i = 0,62542; абсолютная погрешность будет 0,00004. Относительной погрешностью называют отношение абсолютной погрешности к требуемому передаточному числу. В нашем случае относительная погрешность

δ = 0.00004/0,62546 = 0,000065

Следует подчеркнуть необходимость суждения о точности настройки по относительной погрешности.

Общее правило.

Если какая-либо величина А, получаемая настройкой через данную кинематическую цепь, пропорциональна передаточному отношению i, то при относительной погрешности настройки δ абсолютная погрешность будет Аδ.

Например, если относительная погрешность передаточного отношения δ =0,0001, то при нарезании винта с шагом t отклонение в шаге, зависящее от настройки, будет 0,0001 * t. Та же относительная погрешность при настройке дифференциала зубофрезерного станка даст дополнительное вращение заготовки не на требуемую дугу L, а на дугу с отклонением 0,0001 * L.

Если указан допуск на изделие, то абсолютное отклонение размера вследствие неточности настройки должно составлять только некоторую долю этого допуска. В случае более сложной зависимости какой-либо величины от передаточного отношения полезно прибегать к замене фактических отклонений их дифференциалами.

Настройка цепи дифференциала при обработке винтовых изделий.

Типичной является следующая формула:

где с — постоянная цепи;

β — угол наклона винтовой линии;

n — число заходов фрезы.

Продифференцировав обе части равенства, получим абсолютную погрешность di передаточного отношения

тогда допустимая относительная погрешность настройки

Если допустимое отклонение угла винтовой линии dβ выразить не в радианах, а в минутах, то получим

Например, если угол наклона винтовой линии изделия β = 18°, а допустимое отклонение в направлении зуба dβ = 4″ = 0′,067, то допустимая относительная погрешность настройки

δ = 0,067/3440*tg18 = 0,00006

Наоборот, зная относительную погрешность взятого передаточного отношения, можно по формуле (3) определить допущенную погрешность в угле винтовой линии в минутах. При установлении допустимой относительной погрешности можно в подобных случаях пользоваться тригонометрическими таблицами. Так, в формуле (2) передаточное отношение пропорционально sin β. По тригонометрическим таблицам для взятого числового примера видно, что sin 18° = 0,30902, а разность синусов на 1′ составляет 0,00028. Следовательно, относительная погрешность на 1′ составляет 0,00028 : 0,30902 = 0,0009. Допустимое отклонение винтовой линии — 0,067, поэтому допустимая погрешность передаточного отношения 0,0009*0,067 = 0,00006, такая же, как и при расчете по формуле (3). Когда оба сопряженных колеса нарезаются на одном станке и по одной настройке цепи дифференциала, то погрешности в направлении линий зубьев допускаются значительно большие, так как у обоих колес отклонения одинаковы и незначительно влияют только на боковой зазор при зацеплении сопряженных колес.

Настройка цепи обкатки при обработке конических колес.

В этом случае формулы настройки выглядят так:

i = p*sinφ/z*cosу или i = z/p*sinφ

где z — число зубьев заготовки;

р — постоянная цепи обкатки;

φ — угол начального конуса;

у — угол ножки зуба.

Пропорциональным передаточному отношению оказывается радиус основной окружности. Исходя из этого, можно установить допустимую относительную погрешность настройки

где α — угол зацепления;

Δα — допустимое отклонение угла зацепления в минутах.

Настройка при обработке винтовых изделий.

δ = Δt/t или δ = ΔL/1000

где Δt — отклонение в шаге винта за счет настройки;

ΔL — накопленная погрешность в мм на 1000 мм длины резьбы.

Величина Δt дает абсолютную ошибку шага, а величина ΔL характеризует по существу относительную погрешность.

Настройка с учетом деформации винтов после обработки.

При нарезании метчиков с учетом усадки стали после последующей термической обработки или с учетом деформации винта вследствие нагревания при механической обработке, процент усадки или расширения непосредственно указывает на необходимое относительное отклонение в передаточном отношении сравнительно с тем, какое получилось бы без учета этих факторов. В этом случае относительное отклонение передаточного отношения в плюс или минус является уже не ошибкой, а преднамеренным отклонением.

Настройка делительных цепей. Типичная формула настройки

где р — постоянная;

z — число зубьев или других делений на один оборот заготовки.

Нормальный комплект из 35 колес обеспечивает абсолютно точную настройку до 100 делений, так как в числах зубьев колес содержатся все простые множители до 100. В такой настройке погрешность вообще недопустима, так как она равна:

где Δl — отклонение линии зуба на ширине заготовки В в мм;

пD — длина начальной окружности или соответствующей другой окружности изделия в мм;

s — подача вдоль оси заготовки на один ее оборот в мм.

Только в грубых случаях эта погрешность может не играть роли.

Настройка зубофрезерных станков при отсутствии требуемых множителей в числах зубьев сменных колес.

В таких случаях (например, при z = 127) можно настроить гитару деления приближенно на дробное число зубьев, а необходимую поправку произвести, используя дифференциал [5]. Обычно формулы настройки гитар деления, подач и дифференциала выглядят так:

x = pa/z ; y = ks ; φ = c*sinβ/ma

Здесь р, k, с — соответственно постоянные коэффициенты этих цепей; а — число заходов фрезы (обычно а = 1).

Настраиваем указанные гитары согласно формулам

x = paA/Az+-1 ; y = ks ; φ’ = пc/asA

где z — число зубьев обрабатываемого колеса;

А — произвольное целое число, выбираемое так, чтобы числитель и знаменатель передаточного отношения разлагались на множители, подходящие для подбора сменных колес.

Знак (+) или (—) также выбирается произвольно, что облегчает разложение на множители. При работе правой фрезой, если выбран знак (+), промежуточные колеса на гитарах ставятся так, как это делают согласно руководству по работе на данном станке для правовинтовой заготовки; если выбран знак (—), промежуточные колеса ставят, как для левовинтовой заготовки; при работе левой фрезой — наоборот.

Желательно выбирать А в пределах

(1/2)*(пc/as) b+(20. 25); b + d > с+(20. 25) (11)

Эти условия ставятся для предотвращения упора сменных колес в соответствующие валы или детали крепления; числовое слагаемое зависит от конструкции данной гитары. Однако вторая из комбинаций (10) может быть принята только в том случае, когда колесо Z2 устанавливается на первом ведущем валу и если передача z2/z3 замедляющая или не содержит большого ускорения. Желательно, чтобы z2/z3 1) желательно так разбивать i = i1i2 чтобы сомножители были возможно более близкими один к другому и равномернее распределялось повышение скорости. При этом лучше, если i1 > i2

МИНИМАЛЬНЫЕ КОМПЛЕКТЫ СМЕННЫХ КОЛЕС

Состав комплектов сменных колес в зависимости от области применения приведен в табл. 2. В случае особо точных настроек — см. стр. 403.

Числа зубьев минимальных комплектов сменных колес для различных случаев настроек

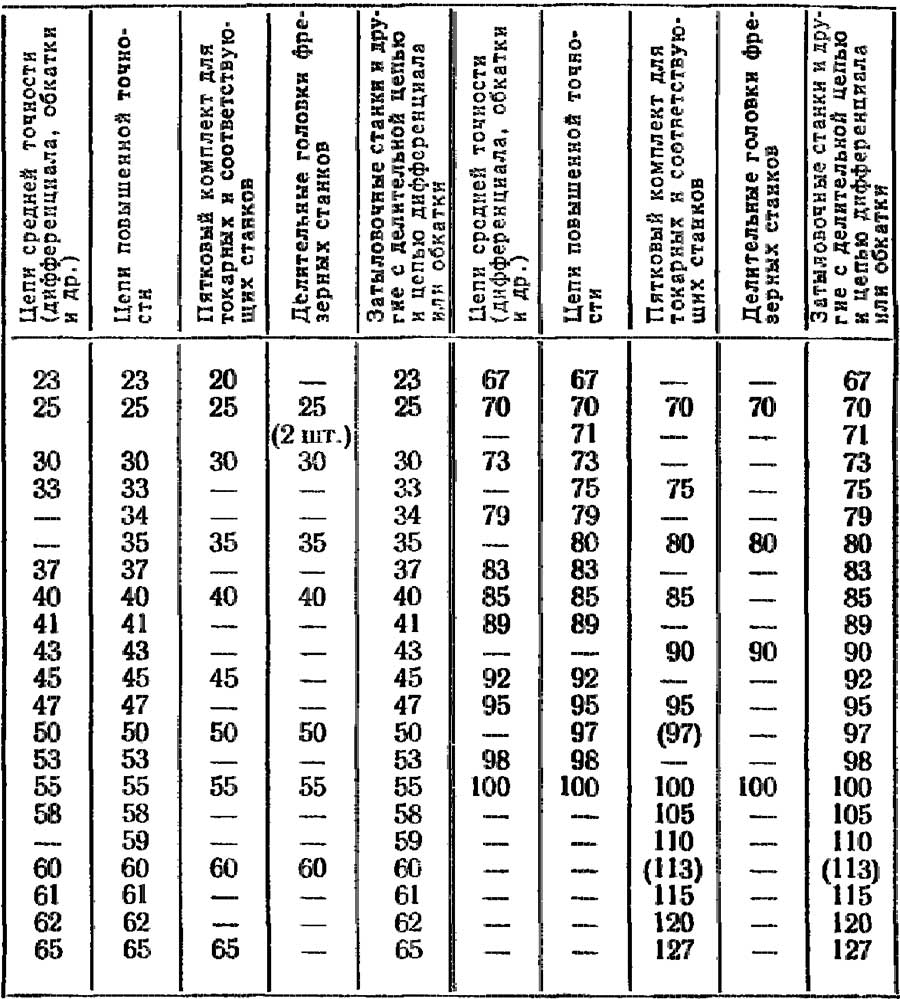
Для настройки делительных головок можно использовать таблицы, прилагаемые заводом. Сложнее, но можно выбирать подходящие пятковые комбинации из приводимых в данной книге «Основных таблиц для подбора зубчатых колес».

Расчет прямозубой шестерни онлайн

Подпишитесь на нашу рассылку!

Geargenerator — онлайн конструктор зубчатого зацепления

Если вы попали на эту страницу, то наверняка знаете программу Gear Template Generator(подробнее о программе). Эта программа позволяет делать расчет параметров зубчатого зацепления. Gear Template Generator устанавливается локально на компьютер и позволяет создавать чертеж пары шестеренок с необходимыми параметрами. (Скачать Gear Template Generator можно тут)

Сейчас я расскажу о аналоге Gear Template Generator – онлайн конструкторе зубчатого зацепления Geargenerator. Собственно если вы введете в адресную строку браузера Geargenerator.com, то попадете на страницу конструктора.

Вот так выглядит начальное окно программы

Окно поделено на две части. Левая часть – панель настроек программы и шестеренок. На правой части будет отображаться результат.

Рассмотрим левую часть

Она условно разделена на несколько блоков с набором параметров. Рассмотрим эти блоки.

Самый верхний блок Animation – анимация движения шестеренок. Старт/стоп, сброс. Можно задать скорость вращения.

Далее идет блок Gears – это список шестеренок и работа с их количеством. По умолчанию там их четыре. Можно добавить, удалить или очистить. Причем новая шестеренка будет добавляться к той, которая выделена в данный момент.

Следующий блок настроек Connection properties – он отвечает за варианты стыковки шестеренок

Поле Parent gear #: — тут можно для текущей шестеренке указать номер родительской шестеренки(из списка Gears). По умолчанию самая первая шестеренка – нулевая. Таким образом можно быстро пере стыковать шестеренки.

Поле Axle connection: — определяет способ стыковки шестеренок. Если установить тут галочку – шестеренки будут стыковаться на одной оси.

Поле Connection angle : — указывает угол на центр шестеренки относительно родительской шестеренки.

Положение шестеренки #1 при значении Connection angle : – 60

Положение шестеренки #1 при значении Connection angle: – 85

Далее Gear properties – параметры самих шестеренок(количество зубьев, параметры зуба и т.д.) В этом же блоке есть самая главная кнопка — Download SVG – клик по ней начинает загрузку файла с шестеренками в формате SVG

Последний блок Display – настройки отображения самого конструктора. Можно поменять цветовую схему, включить/выключить сетку и метки на шестеренках.

Теперь небольшой пример работы

Уменьшим количество зубьев шестеренки #3 до 42

Добавим шестеренку #4 к шестеренке #3 (для этого в блоке Gears нужно кликнуть по #3, а затем по кнопке Add New)

Укажем для #4, что она должна располагаться на одной оси с #3

Добавим к #3 и #4 еще по одному зубчатому колесу с указанием параметра Connection angle (разведем их в стороны)

Нажмем кнопку Start/Stop – и посмотрим на анимацию. Таким образом можно не только собрать нужную последовательность передач, но и подобрать расположение осей шестеренок для дальнейшего размещения в корпусе изделия.

Резюме.

В этом онлайн конструкторе зубчатого зацепления можно выстроить почти весь механизм часов(то, что касается шестеренок). Можно строить достаточно сложные схемы соединения зубчатых колес. В отличие от Gear Template Generator, где можно строить только одну пару шестеренок. Но Gear Template Generator дает большую свободу в настройке параметров шетеренок.

GearGenerator позволяет экспортировать только в SVG.

GearGenerator работает онлайн, не требует установки и бесплатен.

Еще один плюс — все параметры созданного вами зубчатого зацепления добавляются в адресную строку. Сохранить или поделиться результатом своего конструирования можно скопировав текст адресной строки. Пример, который я описывал выше — результат можно увидеть по этой ссылке.

Обе программы обладают своими плюсами. Какую из них выбрать – выбор за вами.

Расчет реечной передачи

Основными звеньями реечной передачи (рис. 3) являются шестерня 1 и зубчатая рейка 2, представляющая собой сектор зубчатого цилиндрического колеса, диаметры делительной и однотипных соосных поверхностей которого бесконечно велики, вследствие чего эти поверхности являются параллельными поверхностями, а концентрические окружности — параллельными прямыми.

Рис. 3. Реечная передача.

Геометрический расчет передачи

Расчет геометрических параметров реечной передачи начинаем с определения делительного диаметра шестерни.

Рассмотрим преобразование вращательного движения шестерни в поступательное движение рейки (рис. 4). Исходными данными для расчета передачи являются: сила сопротивления F₂ = 200 (H) на рейке, перемещение H₂ = 1 (м) и линейная скорость v₂ = 1(м/с) рейки. В этом случае делительный диаметр шестерни 1 на основании условия (3.1)

Передаточное отношение реечной передачи при преобразовании вращательного движения в поступательное рекомендуют принимать U_ВП = 10. 200 1/м.

Поэтому примем U_ВП =100, тогда

Делительный диаметр шестерни можно также найти из условия контактной прочности зубьев, мм:

где К_d = 1.12 — коэффициент прямозубых передач;

F₂ = 200 (H) — сила сопротивления на рейке;

K_Hв = 1.03 — коэффициент, учитывающий неравномерность нагрузки по ширине зуба, определяемый по таблице 1. Данный коэффициент выбираем в соответствии с симметричным расположением шестерни относительно опор. Предположительно, материал с твердостью менее 350 НВ.

ш_bd — коэффициент ширины зубчатого венца, равный 0,2…1,6. В мехатронных модулях желательно принимать ш_bd = 0,2…0,8.

Е_пр = 200 (МПа) — приведенный модуль упругости материалов шестерни и рейки.

[у]_H — допускаемое контактное напряжение, определяемое как

где индекс Н относится к контактным напряжениям, индекс F к изгибным.

Расчет ведем по контактным напряжениям, т.е. по индексу Н.

у_{lim b} — предел выносливости поверхностей зубьев, соответствующий базовому числу циклов перемены напряжений, определяемый по таблице 2. Так как твердость зубьев менее 350 НВ, принимаем предел контактной выносливости у_{lim b} = 2НВ+70 (МПа) и вид термообработки — нормализация, улучшение.

S — коэффициент безопасности.

При нормализации, улучшении и объемной закалке зубьев S_H = 1,1.

К_С — коэффициент, учитывающий реверсивность нагрузки. Так как нагрузка реверсивная, то принимаем К_С = 1,0.

К_L — коэффициент долговечности, учитывающий влияние срока службы и режима нагрузки передачи:

где m — показатель степени. При расчете на контактную прочность принимают m = 3.

N — базовое число циклов изменения напряжений, определяемое из таблицы 3.

N_E — эквивалентное число циклов изменения напряжений. При переменных режимах нагружения (рис.4) вращающим моментом или осевой силой эквивалентное число циклов изменения напряжений за один технологический цикл определяемый по формулам:

Рис.4. Переменные режимы нагружения переменным моментом.

где С = 1 — число реек, находящихся в зацеплении с шестерней;

Т_i — вращающий момент на шестерне на i-ом участке циклограммы нагружения.;

Т_max — максимальный вращающий момент на шестерне по циклограмме нагружения;

F_max — максимальная осевая сила на рейке по циклограмме нагружения;

n_i — частота вращения шестерни на i-ом участке нагружения;

v_i — линейная скорость рейки на i-ом участке нагружения;

t_i — длительность i-го участка нагружения;

d₁ — делительный диаметр шестерни;

k — число участков нагружения.

За весь срок работы передачи:

где Lh — долговечность работы передачи;

t_ц — длительность одного технологического цикла:

При постоянном режиме нагружения формулы для определения эквивалентного числа циклов нагружения принимают вид:

Для зубчатых колес и реек из нормализованных и улучшенных сталей твердостью менее 350 НВ коэффициент доловечности находится в пределах К_HL = 1,0…2,6.

Тогда допускаемое контактное напряжение (3.5):

Рассчитываем делительный диаметр шестерни по формуле (3.4):

Изначально делительный диаметр шестерни, рассчитанный по формуле (3.2), составил 20 (мм). Для обеспечения требуемого передаточного отношения необходимо, чтобы делительный диаметр шестерни, полученный по формуле (3.2), был больше делительного диаметра, найденного по формуле (3.4). Условие выполняется, следовательно, делительный диаметр и передаточное отношение шестерня-рейка выбраны верно.

Вращающий момент на шестерне:

Исходя из расчетов и вида обработки, выбираем материал рейки и шестерни по таблице 4.

Выбираем сталь 45 с выделенными в таблице характеристиками материала.

Определяем модуль зубьев из условия контактной прочности:

где К_m = 6,6 — для прямозубых колес.

Полученное значение модуля зубьев округляем до стандартного значения из таблицы 5.

Выбираем значение модуля зубьев из первого ряда, как наиболее предпочтительного для мехатронных модулей, принимаем m = 2.

Находим число зубьев шестерни:

где cosв = 0 O — угол наклона зубьев.

По значению линейной скорости рейки назначаем степень точности реечной передачи (таблица 6)

Так как передача прямозубая и скорость рейки 1 (м/с), то назначаем 9 пониженную степень точности, которая применяется для тихоходных передач с пониженными требованиями к точности.

Независимо от степени точности зубчатых колес, реек и реечных передач устанавливается шесть видов сопряжений в реечной передаче A, B, C, D, E, H и пять допусков на боковой зазор T_jn, обозначаемых буквами a, b, c, d, h (таблица 7).

Виды сопряжений и гарантированные боковые зазоры.

Выбираем вид сопряжения — В;

Вид допуска на боковой зазор — b.

Для шестерни диаметр окружности вершин зубьев:

Диаметр окружности впадин зубьев:

Толщина зуба шестерни по делительной окружности, равная толщине зуба рейки по средней прямой:

Нормальный шаг зубьев шестерни и рейки:

Минимальная длина нарезанной части рейки:

Минимальное число зубьев рейки:

Округляем число зубьев рейки до целого числа, т.е. 162 зуба.

Уточняем минимальную длину нарезанной части рейки:

Виды зубчатых колес, шестерен

Цилиндрические шестерни

Поперечный профиль зуба

Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. Так как эвольвентное зацепление имеет ряд преимуществ перед остальными: форма этих зубьев соответствует условиям их прочности, зубья легко изготовить и обработать, шестерни не чувствительны к точности установки. Тем не менее, существуют зубчатые передачи с циклоидальной формой профиля зубьев, а так же с шестернями с круговой формой профиля зубьев, например — передача Новикова. Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.

Параметры эвольвентной шестерни:

Модуль шестерни (m) – это основной параметр, который определяется из прочностного расчёта зубчатых передач. Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.

Расчет модуля шестерни:

d — диаметр делительной окружности

z — число зубьев шестерни

d_a — диаметр окружности вершин темной шестерни

d_b — диаметр основной окружности — эвольвенты

d_f — диаметр окружности впадин темной шестерни

В машиностроении приняты стандартные значения модуля зубчатого колеса для удобства изготовления и замены зубчатых колёс, представляющие собой числа от 1 до 50.

Высота головки зуба — h_aP и высота ножки зуба — h_fP в случае, так называемого, «нулевого» зубчатого колеса соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,2 m, то есть:

Отсюда получаем, что высота зуба h = 2,2m

Так же можно практически вычислить модуль шестерни, при этом, не имея всех данных для определения модуля, по следующей формуле:

Продольная линия зуба

Прямозубые шестерни

Прямозубые шестерни — самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.

Косозубые шестерни

Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.

Шевронные колёса

Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами — плавающих опорах.

Шестерни с внутренним зацеплением

Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.

Винтовые шестерни

Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.

Секторные шестерни

Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.

Шестерни с круговыми зубьями

Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.

Конические шестерни

Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Звездочка

Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.

Коронная шестерня

Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.