Модуль объемной упругости формула

Модуль упругой деформации

Определение и модуль упругой деформации

Деформация в твердом теле называется упругой, если она пропадает после того, как нагрузку с тела сняли.

В общем случае модуль упругости (E) определяют как

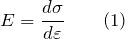
где – напряжение; – относительная деформация. Надо помнить, что данное определение справедливо для линейного отрезка диаграммы напряжений, то есть когда деформацию можно считать упругой. На данном участке диаграммы величина E определена тангенсом угла наклона прямолинейного участка диаграммы.

В зависимости от типа деформации, направления действия деформирующей силы различают несколько модулей упругости. Наиболее часто используемые:

1. модуль Юнга;
2. модуль сдвига;
3. модуль объемной упругости;
4. коэффициент Пуассона и др.

Модуль Юнга

Модуль Юнга используют при характеристике деформация растяжения (сжатия) упругого тела, при этом деформирующая сила действует по оси тела. Модуль Юнга чаще всего определяют используя закон Гука:

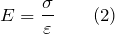
Модуль Юнга, равен напряжению, появляющемуся в стержне, если его относительное удлинение равно единице (или 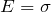при двойном удлинении длины тела). На практике кроме резины при упругой деформации двойного удлинения невозможно достичь, тело рвется.

Коэффициент упругости и модуль Юнга связаны как:

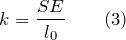
где 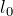– длина тела до деформации; S – площадь поперечного сечения.

Единицей измерения модуля Юнга служит паскаль.

Модуль сдвига

При помощи модуля сдвига (G) характеризуют способность тела оказывать сопротивление изменению формы тела (при этом объем сохраняется). Находят модуль сдвига как:

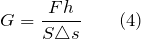
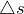– абсолютный сдвиг слоев параллельных по отношению друг к другу; h — расстояние между слоями; F – сила, вызывающая сдвиг, параллельная сдвигающимся слоям тела.

Если вещество является однородным и изотропным, то модуль сдвига связан с модулем Юнга выражением:

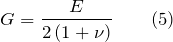
где 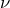– коэффициент Пуассона для материала, который зависит от природы вещества. Иногда обозначается буквой .

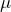Модуль объемной упругости

Модуль объемной упругости (модуль объемного сжатия) (K) – отражает способность тела к изменению объема при действии объемного напряжения, которое одинаково по всем направлениям. Его определяют выражением:

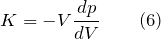
где V – объем тела; p – давление, оказываемое на тело.

Если тело является изотропным, то:

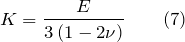
Примеры решения задач

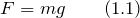
Абсолютное удлинение растянутого тела связано с модулем упругости выражением:

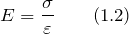
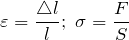
То есть формула (1.2) преобразуется к виду:

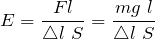
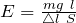
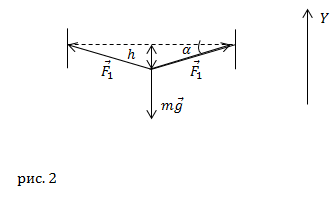
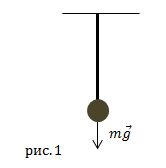
В равновесии мы имеем (см. рис.1):

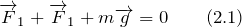
где 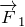– сила натяжения проволоки. В проекции на ось Y:

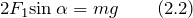
Так как угол 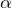мал, то можно считать:

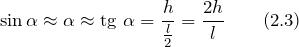
Используя выражения (2.2) и (2.3) запишем:

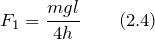
Модуль Юнга для нашего случая равен:

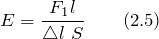
где удлинение проволоки найдем как:

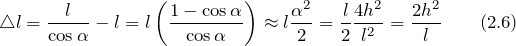
Подставим в (2.5) формулы (2.4) и (2.6), имеем:

Объёмный модуль упругости

Объёмный модуль упругости (K) характеризует способность вещества сопротивляться всестороннему сжатию. Эта величина определяет, какое нужно приложить внешнее давление для уменьшения объёма в 2 раза. Например, у воды объёмный модуль упругости составляет около 2000 МПа — это означает, что для уменьшения объёма воды на 1 % необходимо приложить внешнее давление 20 МПа. С другой стороны, при увеличении внешнего давления на 0,1 МПа объём воды уменьшается на 1/20000 часть. Единицей измерения объёмного модуля упругости является Паскаль (Па). [1]

Содержание

Определение

Объёмный модуль упругости K>0 может быть определён по формуле:

Величина, обратная объемному модулю упругости, называется коэффициентом объёмного сжатия.

Термодинамические соотношения

Строго говоря, объёмный модуль упругости является термодинамической величиной, и необходимо определить объёмный модуль упругости в зависимости от условий изменения температуры: при постоянной температуре (изотермический ), при постоянной энтропии (адиабатический ) и т. д. В частности, подобные различия обычно важны для газов.

Для газа адиабатический объёмный модуль упругости приближённо даётся формулой

и изотермический объёмный модуль упругости приближённо равен

Для жидкостей объёмный модуль упругости K и плотность ρ определяют скорость звука c (волны давления (англ.)), согласно формуле Ньютона-Лапласа

Измерение

Можно измерить объёмный модуль упругости с помощью порошковой рентгеновской дифракции.

Некоторые значения

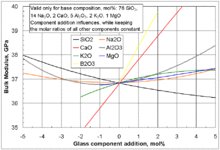
Примечания

1. ↑Bulk Elastic Properties. hyperphysics. Georgia State University. Архивировано из первоисточника 30 августа 2012.
2. ↑ (1985) «Calculation of bulk moduli of diamond and zinc-blende solids». Phys. Rev. B32: 7988–7991. DOI:10.1103/PhysRevB.32.7988. Bibcode: 1985PhRvB..32.7988C.
3. ↑Fluegel, AlexanderBulk modulus calculation of glasses. glassproperties.com. Архивировано из первоисточника 30 августа 2012.

Модуль объёмной упругости () | Модуль Юнга () | Параметры Ламе () | Модуль сдвига () | Коэффициент Пуассона () | en:P-wave modulus ()

Wikimedia Foundation . 2010 .

Смотреть что такое «Объёмный модуль упругости» в других словарях:

Модуль — (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия

Модуль сдвига — Сдвиговая деформация В материаловедении модулем сдвига (обозначается буквой G или μ), называется отношение касательного напряжения к сдвиговой деформации … Википедия

МОДУЛЬ — (от лат. modulus мера) 1) назв. к. л. особо важного коэффициента или величины (напр., модуль зубьев, модуль упругости, М. комплексного числа). 2) Условная единица в стр ве и архитектуре, принимаемая для выражения кратных соотношений размеров… … Большой энциклопедический политехнический словарь

Модули упругости — величины, характеризующие упругие свойства материала. В случае малых деформаций, когда справедлив Гука закон, т. е. имеет место линейная зависимость между напряжениями и деформациями, М. у. представляют собой коэффициент… … Большая советская энциклопедия

МОДУЛИ УПРУГОСТИ — (от лат. modulus мера), величины, характеризующие упругие св ва материалов при малых деформациях. При растяжении силой F цилиндрич. образца длиной l с площадью поперечного сечения 5 имеет место линейная зависимость между норм. напряжением в… … Физическая энциклопедия

Напряжение сдвига — У этого термина существуют и другие значения, см. Напряжение. Напряжённому состоянию чистого сдвига, при котором по двум взаимно перпендикулярным площадкам действуют только касательные напряжения , соответствует модуль сдвига . Модуль сдвига… … Википедия

Теллурид ртути — Кристалличесая структура HgTe типа сфалерита … Википедия

СЖИМАЕМОСТЬ — способность в ва изменять свой объём под действием всестороннего давления. С. обладают все в ва. Если в во в процессе сжатия не испытывает хим., структурных и др. изменений, то при возвращении внеш. давления к исходному значению нач. объём… … Физическая энциклопедия

Резина (продукт вулканизации каучука) — Резина (от лат. resina ‒ смола), вулканизат, продукт вулканизации каучука (см. Каучук натуральный, Каучуки синтетические). Техническая Р. ‒ композиционный материал, который может содержать до 15‒20 ингредиентов, выполняющих в Р. разнообразные… … Большая советская энциклопедия

Резина — I Резина (от лат. resina смола) вулканизат, продукт вулканизации (См. Вулканизация) каучука (см. Каучук натуральный, Каучуки синтетические). Техническая Р. композиционный материал, который может содержать до 15 20 ингредиентов,… … Большая советская энциклопедия

Модуль Юнга (упругости)

Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Основные сведения

Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.

Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)

Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.

График теста на растяжение

E- это частное от деления нормальных напряжений σ на относительное удлинение ε.

Закон Гука также можно сформулировать и с использованием модуля Юнга.

Физический смысл модуля Юнга

Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.

Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.

В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:

Величину, обратную α, и называют модулем Юнга:

ε = (Δl) / l = α * (F/S)

Отношение растягивающей силы F к S называют упругим напряжением σ:

Закон Гука, записанный с использованием модуля Юнга, выглядит так:

Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.

В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.

Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l

Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.

Значения модуля юнга для некоторых материалов

В таблице показаны значения E ряда распространенных веществ.

Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.

Предел прочности материала

Это предел возникающего напряжения, после которого образец начинает разрушаться.

Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности

Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.

Допускаемое механическое напряжение в некоторых материалах при растяжении

Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.

Испытание на растяжение

Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.

Большая Энциклопедия Нефти и Газа

Модуль — объемная упругость

К сожалению, опубликованные в литературе формулы для расчета суммарного модуля объемной упругости газо-жидкостной смеси не всегда дают точные результаты. Так, методика, приведенная в работе [ 61 I, не учитывает зависимости объемов жидкой и газовой фазы от давления в рассматриваемой замкнутой полости. [31]

При количестве газа, достаточном для образования отдельной фазы, модуль объемной упругости значительно снижался; присутствие же только растворенного водорода вызывало лишь небольшое снижение модуля. Практически это означает, что давление в гидравлической системе должно поддерживаться выше давления насыщения для ожидаемого количества газа. [32]

Обозначения х — коэффициент сжимаемости материала, К, — модуль объемной упругости , р — интенсивность распределенной нагрузки по площади. [33]

Существует большая путаница в отношении использования и толкования данных определения модулей объемной упругости , опубликованных в технической литературе. Это объясняется отсутствием точного определения условий, в которых производятся измерения. [34]

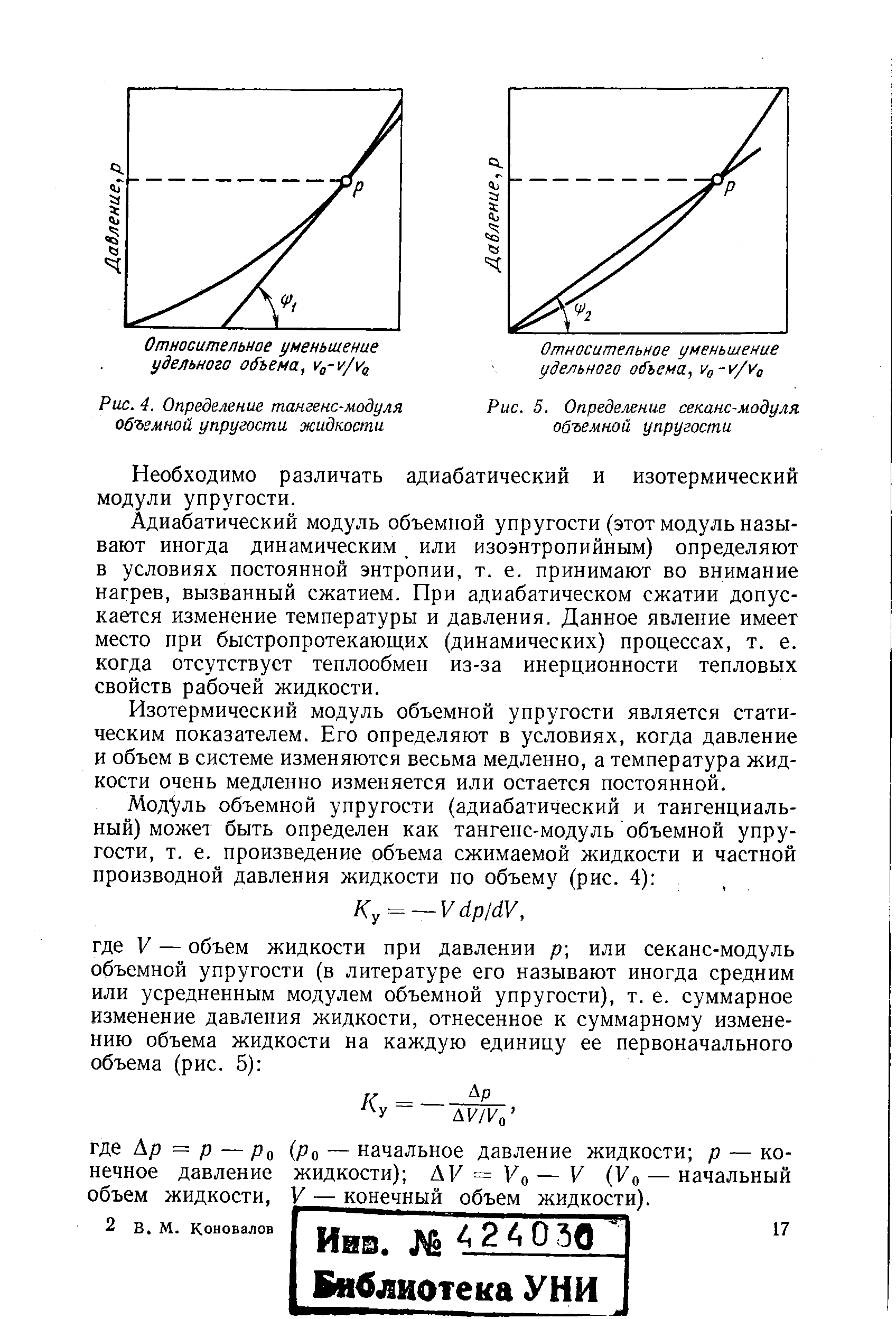
Секанс-модуль объемной упругости ( часто называемый в литературе средним или усредненным модулем объемной упругости ) определяется как суммарное изменение давления жидкости, отнесенное к суммарному изменению объема жидкости на каждую единицу ее первоначального объема под давлением. [35]

В связи с растворимостью в жидкости воздуха, приводящей к понижению ее модуля объемной упругости и повышению сжимаемости, целесообразно применять системы, содержащие малые количества жидкости. [36]

Большая часть расчетов гидравлических систем основывается на использовании величины обратной сжимаемости — модуля объемной упругости . Чем он выше, тем менее податлива и более жестка жидкость. Собственная частота колебания системы пропорциональна квадратному корню из модуля объемной упругости. Таким образом, при повышении жесткости жидкости собственная частота возрастает. [37]

В твердых телах продольные волны опережают поперечные, так как в большинстве случаев модуль объемной упругости значительно. [38]

В твердых телах продольные волны опережают поперечные, так как в большинстве случаев модуль объемной упругости значительно превы-шает по величине модуль сдвига. [39]

Когда при повышении внутриглазного давления вследствие конвергенции и изменения формы глазного яблока увеличивается модуль объемной упругости склеры ( Е), это означает, что усиливаются упругие силы, препятствующие ее растяжению. В определенной мере величина El характеризует уровень этих упругих сил. После возвращения глаз из конвергентного положения в обычное упругие силы в склере уменьшаются до соответствия обычному для данной склеры модулю ее объемной упругости. Это означает и возвращение глаз к их обычной сферической форме — конвергентная ( временная) миопия исчезает. [40]

Ввиду того, что равновесие в жидкости при со 0 устанавливается с запаздыванием, модуль объемной упругости оказывается больше, чем при равновесных процессах, и называется адиабатическим Еа. При частоте ю 0 модуль объемной упругости называется равновесным или изотермическим Еп. Следствием релаксации может быть изменение демпфирующих свойств и потеря устойчивости привода при отсутствии активных сопротив-лений. [41]

Со второй половины XIX века появилось несколько попыток непосредственного определения коэффициента Пуассона v и модуля объемной упругости К — Довольно рано было осознано, что вычисление этих величин по экспериментально найденным значениям Е и ( г приводит не только к весьма различающимся, но во многих случаях явно неверным значениям. [42]

Подставив в (1.32) выражения для Я и i (I.27) и (1.28), получим связь модуля объемной упругости / ( с модулем Юнга Е и коэффициентом Пуассона v0: К. [43]

Из-за различия значений Аи и В процессы при разных частотах будут отличаться друг от друга ( модуль объемной упругости рабочей жидкости зависит не только от давления и температуры, но и от частоты), что может сделать использование частотных методов расчета динамических процессов некорректным. Однако материалов о зависимости модуля объемной упругости от частоты применительно к реальным установкам пока еще недостаточно. [44]

Известны такие упругие постоянные изотропного тела, как модуль Юнга, коэффициент Пуассона, модуль Жесткости, модуль объемной упругости , коэффициент сжимаемости, однако лишь две из них независимы. Понятие об этих параметрах и их взаимозависимостях служит основой для изучения материалов, предназначенных для электроакустики и ультразвуковой техники. [45]

Справочник химика 21

Химия и химическая технология

Модуль упругости жидкости

Иногда вместо коэффициента объемного сжатия вводят модуль упругости жидкости = 1/Р . Формулы (2.28) и (2.29), выраженные через модуль упругости примут следующий вид [c.49]

Локальный объемный модуль упругости жидкости в общем случае зависит от температуры, давления жидкости н скорости процесса объемной деформации. Путем обобщения известных формул и графиков 1, 3, 5, 21, 31 ] получена приближенная вависимость для определения локального модуля упругости жидкости [c.131]

Дополнительно воспользуемся полученным ранее уравнением р dp — пр dp =0 и общепринятым выражением для локального модуля упругости жидкости [311 [c.129]

I — текущее время Е — приведенный модуль упругости жидкости и стенок трубопровода р — плотность жидкости С — коэффициент гидравлических потерь давления, отнесенных к единице длины трубопровода. [c.364]

Е — модуль упругости жидкости в кГ/м [c.162]

Если аппарат работает без подпора, т. е. Pst = О, то, учитывая взаимосвязь модуля упругости жидкости со скоростью звука в ней, получим конечное выражение, связывающее длину дуги преобразования с геометрическими и кинематическими параметрами аппарата [c.66]

При плавлении твердого тела происходит скачок в величине текучести. Наличие этого свойства не является качественным отличием жидкости от твердого тела, так как последнее обладает ползучестью. Вместе с тем механизм ползучести совершенно отличен от механизма текучести. Наличие упругости у твердого тела ие является его качественным отличием от жидкости. Жидкость также можно упруго расширять и сжимать. Од1 ако измерению подобных явлений изменений препятствует текучесть жидкости. Если, однако, тщательно заполнить жидкостью некоторый, предварительно откачанный сосуд, а затем охладить его, то жидкость не оторвется от стенок из-за уменьшения объема и окажется растянутой. Такнм путем измеряли модуль упругости жидкости. Потеря дальнего порядка при плавлении определяет скачкообразное изменение свойств жидкости. Объяснение скачкообразности переходов является одной пз задач теории жидкого состояния. Основным отличием жидкости от газа является наличие границы между жидкого [c.207]

Перечисленные утечки являются наружными. Их можно измерить, выпуская из корпуса через специальный дренаж. Внутренние утечки д из полости в полость Р1 через перемычки распределителя (см. рис. 4-15, в) измерены быть не могут. Поэтому полные утечки в насосе 1, и объемные потери в гидромоторе д можно только вычислить при известных значениях е,, и е. пользуясь выражениями (4-6), (4-44) и (4-20). При этом для насоса, если влияние сжимаемости ощутимо, необходимо определить по формуле (4-79), пользуясь модулем упругости жидкости и, что позволит оценить мощность объемных потерь Мд по выражению (4-36) или (4-43). [c.301]

Величина, обратная коэффициенту Рр, называется модулем упругости жидкости [c.72]

Заменяя коэфициент сжимаемости к модулем упругости жидкости — получаем [c.143]

Е — модуль упругости жидкости в кГ/м е — относительная деформация резинового покрытия при сжатии. [c.162]

В-третьих, на входе в трубе сами молекулы, попадая в область с каким-то градиентом скорости, деформируются и ориентируются в направлении потока. Этот процесс деформации молекул также требует дополнительной затраты энергии. Его следует учитывать, сообразуясь с модулем упругости жидкости. [c.65]

К н Е — соответственно модули упругости жидкости и материала трубы в н/м -, [c.117]

Здесь Е — модуль упругости жидкости к — осевой размер камеры. Величины остальных расходов определяются по формулам (7.49). Из формул (7.54) видно, что расходы (З1 и Рг — нелинейные функции X. Поэтому первое уравнение баланса расходов нужно линеаризовать, записав его в вариациях [c.388]

I —модуль упругости жидкости, равный для воды 2,1-104 кг1см [c.255]

V — удельный вес жидкости го — внутренний радиус тонкостенного трубопровода до гидравлического удара с — скорость движения жидкости в трубе 6—толщина стенки трубопровода 1 модуль упругости жидкости 2 — модуль упругости материала стенок трубопровода Г — наружный радиус толстостенной трубы Г2 = внутренний радиус толстостенной трубы. [c.103]

Сопротивление растяжению жидкостей мо>ц,ет возникать только в дегазированных жидкостях. В опытах удавалось при центрифугировании дегазированной дистиллированной воды получить на очень короткое время напряжения растяжения в воде, доходившие приблизительно до 25 МПа. Технические жидкости не сопротивляются растягивающим усилиям. Газы могут находиться в жидкости в растворенном и нерастворенном виде. Присутствие в жидкости нерастворенного воздуха (газа) в виде пузырьков существенно уменьшает модуль упругости жидкости, причем это уменьшение не зависит от размеров пузырьков воздуха. Динамическая вязкость жидкости с увеличением содержания воздуха растет. Содержание нерастворенного воздуха в рабочих жидкостях гидросистем машин и механизмов, так же как и в трубопроводах, подающих жидкость, может сильно повлиять на параметры работы трубопроводов и гидросистем. [c.17]

Что такое модуль упругости жидкости [c.25]

При выводе основных уравнений теории упругого режима мы предполагали, что деформация скелета пористой среды при изменении давления в пласте является упругой (т.е. обратимой при снятии нагрузки) и более того — линейно-упругой. Казалось бы, для этого есть все основания, поскольку изменения давления в процессе разработки пласта малы по сравнению с модулями упругости жидкости и материала пористого скелета, а сам материал скелета обычно является вполне хрупким телом, деформирующимся упруго вплоть до разрушения. [c.245]

Величина, обратная р, называется объемным модулем упругости жидкости при всестороннем сжатии [c.41]

Ввиду высокого значения объемного модуля упругости жидкостей в ряде технических расчетов сжимаемостью при типовых давлениях ( 1,3-10 Н/м ) даже незначительное сжатие жидкости приводит к возникновению значительных нагрузок. [c.138]

Е — модуль упругости жидкости (см. стр. 40) р — давление сжатия под действием обратного потока жидкости в камере. [c.290]

Приведенный объемный модуль упругости жидкости для случая тонкостенного трубопровода ( — заполненного жид- [c.482]

В некоторых случаях подачу насоса Q измеряют по объему жидкости, находящейся под действием конечного давления. Разница в объемах одного и того же количества жидкости ДРсж = = Q (р — р )1Е , где — модуль упругости жидкости. [c.110]

Коеффициенты формулы (2.102) модуля упругости жидкости [c.132]

Величина а зависит от материала стенок, размеров трубопровода и объемного модуля упругости жидкости. Если учесть значение объемного модуля упругости воды, равное 2,1X10 кг/см , средней плотности воды и ускорения свободного падения, то а можно определить по формуле [c.366]

На режим работы отрицательно влияет также превышение угла фз над углом ф . Отрицательное действие перекрытий в этом случае обусловлено тем, что при наличии угла запаздывания фд поршень на некоторой части хода в процессе нагнетания (вытеснения жидкости) будет перемещаться при перекрытом окне цилиндра. В результате, если фз > ф , поршень, выбрав недозапол-ненное вследствие наличия ф пространство цилиндра, будет при дальнейшем движении сжимать жидкость в последнем (явление компрессии). При этом, вследствие высокого модуля упругости жидкости, изменения давления в цилиндре могут достигать больших величин даже при очень малых перемещениях поршня в отсеченном цилиндре в направлении уменьшения его объема (см. стр. 40). Давление в этом случае повысится до такого значения, при котором будет обеспечен ход поршня за счет утечки жидкости через зазоры и за счет упругих деформаций жидкости в объемах элементов насоса. [c.138]

Смотреть страницы где упоминается термин Модуль упругости жидкости: [c.6] [c.64] [c.333] [c.131] [c.326] [c.40] [c.208] [c.138] [c.394] [c.218] [c.371] [c.13] [c.62] [c.5] [c.122] [c.482] Лабораторный курс гидравлики, насосов и гидропередач (1974) — [ c.287 , c.324 , c.333 ]

Теория и проектирование гидро- и пневмоприводов (1991) — [ c.62 , c.131 ]

Тепло- и массообмен Теплотехнический эксперимент (1982) — [ c.12 ]

Энциклопедия по машиностроению XXL

Оборудование, материаловедение, механика и .

Модуль объемной упругости жидкости

Модуль объемный упругости жидкости 8 Напор 54, 55, 74 [c.236]

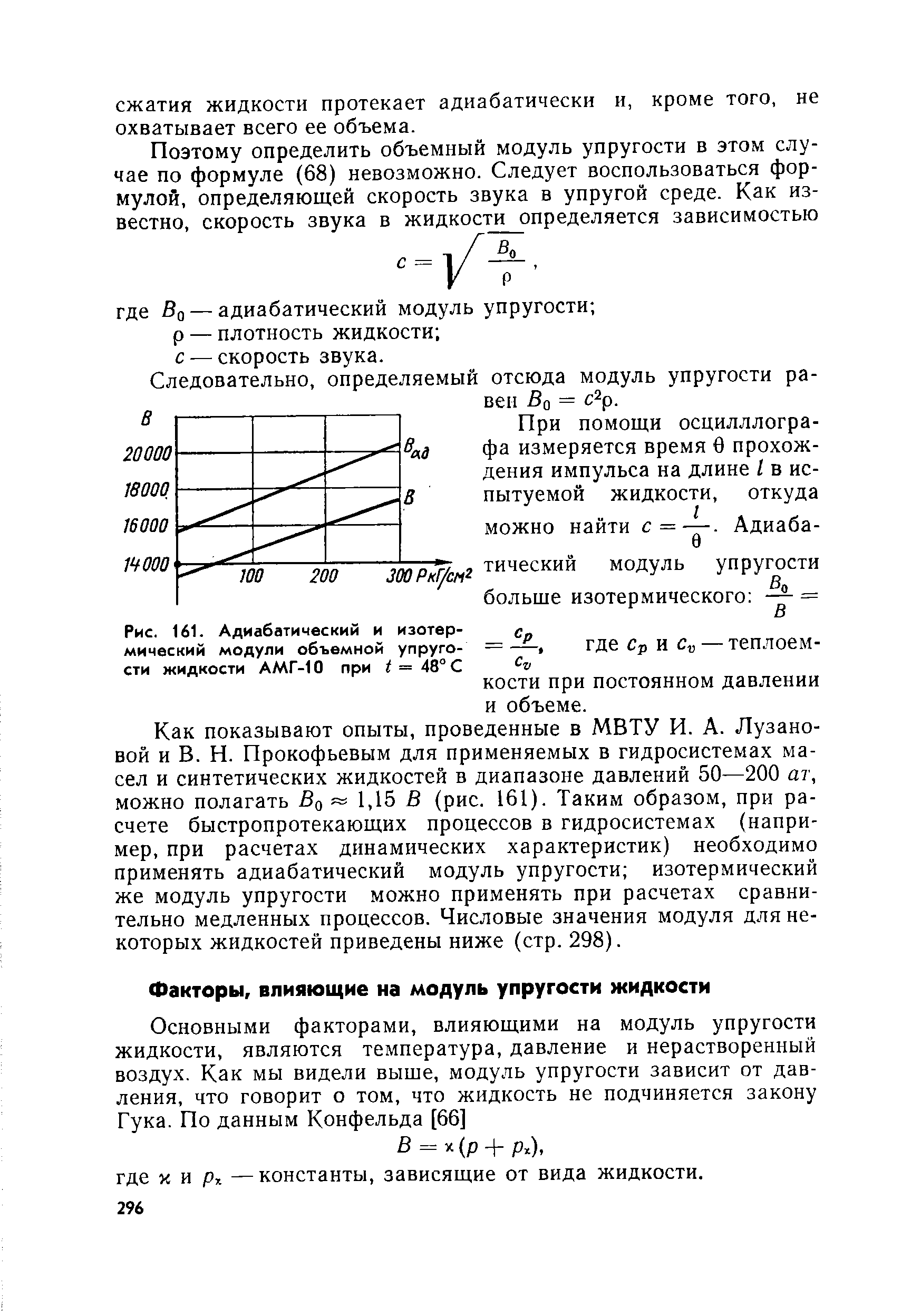
X — приведенное значение модуля объемной упругости жидкости, способ вычисления которого был подробно рассмотрен в 4.10. [c.200]

Модуль объемной упругости жидкости можно измерять статическим и динамическим методами. Статический модуль [c.112]

Работа гидравлических систем протекает в динамических условиях. Поэтому так называемый динамический или тангенс-модуль объемной упругости жидкости, вероятно, более применим при определении быстродействия системы, чем секанс-модуль. Относительно кратковременные периоды пульсации по времени недостаточны для поглощения жидкостью тепла извне или передачи тепла жидкостью за пределы системы. Сжатие и декомпрессию жидкости в элементах системы в этом случае следует считать адиабатическими, и система может рассматриваться как адиабатическая. Следовательно, важным оказывается изоэнтропийный (адиабатический) модуль всесторонней объемной упругости. Если элементы системы движутся медленно, создаются изотермические условия и становится возможным использовать изотермический модуль объемной упругости. [c.118]

При теоретических исследованиях допустимо пользоваться изотермическим модулем объемной упругости жидкости. Динамическая схема при этом совпадает со схемой [c.438]

Скорость распространения упругих возмущений в трубопроводе зависит от модуля объемной упругости жидкости и от характеристик трубопровода [c.120]

ГД0 Р — давление при р == ро, Г — параметр, характеризующий отклонение адиабатической сжимаемости жидко сти от закона Гука. Как Р,, так и Г являются эмпирическими постоянными. Из экспериментальных результатов следует, что величина Р имеет порядок нескольких тысяч атмосфер, а Г для разных жидкостей изменяется от 4 до 12 (см. табл, 4 на стр. 166, где приведены значения п == Г для жидкостей, измеренные акустическими методами). Величина Р,, определяющая адиабатический модуль объемной упругости жидкости. [c.20]

Величина, обратная коэффициенту сжимаемости (1/Рг), называется модулем объемной упругости жидкости и обозначается символом К. Единицей измерения модуля объемной упругости является ньютон на квадратный метр (Н/м ). Модуль объемной упругости, как и коэффициент сжимаемости, непостоянен. Он изменяется в зависимости от давления и температуры. Средние значения коэффициента сжимаемости некоторых жидкостей при давлениях до 5000-10 Па приведены в табл. 1.4. [c.13]

В этих формулах — приведенный модуль объемной упругости жидкости и трубы [см. (36.114)] =// — объем жидкости в трубе. Подставляя (42.13) и (42.14) в (42.12), получи.м полную энергию положительной полуволны [c.540]

Таким образом, модуль объемной упругости идеального газа при постоянной температуре равен давлению, тогда как модуль объемной упругости жидкости при постоянной температуре не зависит от давления. Поведение сжимаемого газа напоминает нелинейную пружину, тогда как сжимаемая жидкость ведет себя подобно линейной пружине. С другой стороны, модуль объемной упругости идеального газа не зависит от температуры, тогда как модуль упругости больщинства жидкостей сильно меняется с температурой. [c.100]

Рассмотрим идеальный гидродвигатель без трения и утечек, соединенный с управляющим золотником двумя трубопроводами. Допустим, что гидросистема заполнена однородной жидкостью под сравнительно высоким давлением и что золотник герметично перекрывает входные отверстия в трубопроводы. Если бы жидкость была несжимаемой, то вал гидромотора оказался бы жестко закрепленным. Если жидкость, как и все реальные жидкости, окажется в какой-то степени сжимаемой, то вал можно будет повернуть, при этом гидромотор будет действовать как насос, повышая давление в одном соединительном трубопроводе и понижая в другом. Момент, необходимый для поворота вала гидромотора, будет пропорционален перепаду давлений в трубопроводах, а угол поворота вала — изменению объемов полостей гидромотора, соединенных с трубопроводами. При той степени точности, когда модуль объемной упругости жидкости принимают за постоянную величину, можно считать, что вал гидромотора соединен с пружиной постоянной жесткости. Крутизну кривой, характеризующей пружину, можно вычислить. [c.139]

Даны следуюш,ие величины рабочий объем насоса V = = 10 см максимальная частота вращения вала насоса rtmax = 960 об/мин длина напорной гидролинии /=10 м диаметр трубопровода d=16 мм толщина стенок трубы б = = 1 мм модуль упругости материала труб F=10 МПа модуль объемной упругости жидкости К=10 МПа объемный к.п.д. насоса при частоте вращения я=1000 об/мин и давлении р = [c.101]

В соответствии с этим будут различными для этих процессов и величины модуля упругости, причем модуль упругости при политропиом и адиабатном процессах будет ниже, чем при изотермном. Для обычных условий работы гидросистем управления разница менаду этими величинами обычно бывает незначительной и ею пренебрегают. Однако для некоторых случаев, и в особенности при высоких температурах, для некоторых рабочих жидкостей при расчетах необходимо учитывать количественное различие между изотермной и политропной сжимаемостью, так как даже небольшая ошибка может вследствие большого изменения модуля объемной упругости жидкости при нагревании изменить характеристику системы и привести к нарушению работы и в частности к потере ею устойчивости. [c.30]

Обратный поток жидкости из нагнетательной полости насоса рабочую камеру и сопровождающие его забросы давления будут наблюдаться, хотя и в меньшей мере, также и в случае полного заполнения цилиндров жидкостью при проходе зоны всасывания. Обратный поток в этом случае вызывается тем, что для сжатия заюхюченной в цилиндре жидкости до выходного давления в него из полости нагнетания насоса должен поступить некоторый объем жидкости, величина которого определится в основном перепадом давления в полостях всасывания и нагнетания насоса, а также пр аведенным модулем объемной упругости жидкости (рабочей сре ы) и объемом цилиндра. [c.309]

Модулем объемной упругости жидкости К называется величина, обратная коэффициенту объемного сжатия. Модуль объемной упругости воды при повышении температуры от О до 20°С увеличивается примерно на 10%. Для обычных условий, в которых работают гидротехнические соорух Смотреть страницы где упоминается термин Модуль объемной упругости жидкости : [c.106] [c.225] [c.138] [c.106] [c.188] [c.14] [c.360] [c.177] [c.492] [c.67] [c.362] [c.318] [c.475] [c.50] [c.268] [c.100] [c.289] [c.332] [c.339] [c.347] [c.359] [c.397] [c.26] Гидравлика (1982) — [ c.14 ]