Максимальная кинетическая энергия груза формула

Механические колебания. Пружинный маятник

Механическими колебаниями называются движения, характеризующиеся определенной повторяемостью во времени.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Гармоническими называются колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (или косинуса).

Пружинный маятник – это колебательная система, состоящая из груза массой т, закрепленного на пружине, совершающая гармонические колебания под действием упругой силы 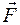, зависящей от величины линейной деформации x по закону Гука (F_x = – kx, где k – жесткость пружины.

Согласно второму закону Ньютона уравнение движения маятника:

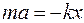Так как ускорение a является второй производной от смещения x (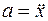), то

или .

Если обозначить 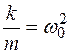, то получим дифференциальное уравнение свободных незатухающих гармонических колебаний пружинного маятника:

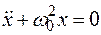Решением этого дифференциального уравнения является функция x(t):

где – отклонение тела от положения равновесия в момент времени t;

А – амплитуда колебания, то есть максимальное отклонение колеблющегося тела от положения равновесия;

w – круговая (циклическая) частота;

j – начальная фаза колебания.

Круговая частота , где Т – период колебаний: .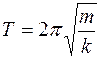

Кинетическая энергия колебаний пружинного маятника:

Потенциальная энергия колебаний пружинного маятника:

Полная энергия колебаний пружинного маятника:

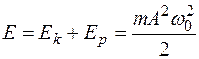откуда видно, что полная энергия свободных незатухающих гармонических колебаний пружинного маятника остается со временем постоянной.

Свободные затухающие гармонические колебания пружинного маятника (рис. 6). Для пружинного маятника массой т, совершающего колебания под действием упругой силы 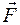(F_x = – kx)с учетомсилы сопротивления 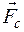, пропорциональной скорости 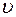движения груза (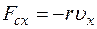), второй закон Ньютона имеет вид:

где r – коэффициент сопротивления.

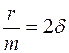Обозначив и ( – коэффициент затухания), получим дифференциальное уравнение свободных затухающих гармонических колебаний пружинного маятника:

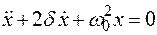Решением этого дифференциального уравнения в случае малых затуханий

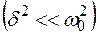является функция x(t):

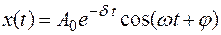где – амплитуда затухающих колебаний в момент времени t;

– начальная амплитуда, т.е. амплитуда в момент времени t = 0,

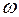– круговая (циклическая) частота: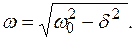

Период затухающих гармонических колебаний пружинного маятника:

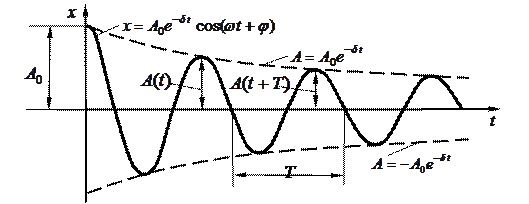
Декремент затухания. Если A(t)и А(t+Т) – амплитуды двух последовательных колебаний (рис. 6), то отношение этих величин называется декрементом затухания .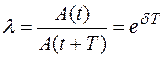

Логарифм называется логарифмическим декрементом затухания :

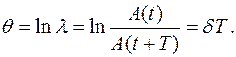
188.64.169.166 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Пружинный и математический маятник

Примерами гармонических колебаний служат колебания пружинного и математического маятников.

Пружинный маятник — тело массой т, колеблющееся на упругой пружине (рис. 5.5) и совершающее гармонические колебания под воздействием упругой силы:

где к — жесткость пружины.

Закон движения пружинного маятника:

где а — угол отклонения маятника от положения равновесия; а — амплитуда колебаний (максимальное значение угла отклонения).

При последовательном соединении пружин (рис. 5.5, б) общий коэффициент жесткости

При параллельном соединении пружин общий коэффициент жесткости (рис. 5.5, в)

Круговая (циклическая) частота:

Кинетическая энергия пружинного маятника:

Потенциальная энергия пружинного маятника:

Полная энергия пружинного маятника:

На рис. 5.6, а представлен график зависимости потенциальной энергии Е_п пружинного маятника от деформации х, где Е — полная энергия (прямая горизонтальная линия), кинетическая Е_к и потенциальная Е_п энергии заданы соответствующими отрезками ординат. Из рисунка следует, что с возрастанием деформации х потенциальная энергия маятника возрастает, кинетическая — уменьшается (и наоборот). В отсутствие трения полная энергия тела сохраняется (Е = Е_к + Е_и) при любых значениях х

Графические зависимости кинетической Е_к, потенциальной Е_п и полной энергий Е упругой деформации тел от времени t показаны на рис. 5.6, б.

Математический маятник — материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной I и колеблющаяся под действием силы тяжести (рис. 5.7).

Круговая (циклическая) частота:

Период и частота колебания математического маятника:

Если маятник движется вниз с ускорением а (или вверх с замедлением а), его период

Если маятник движется вверх с ускорением а (или вниз с замедлением а), его период

Если маятник движется с ускорением а в горизонтальном направлении, его период

Кинетическая энергия математического маятника:

Потенциальная энергия математического маятника:

Превращение энергии при гармонических колебаниях происходит в соответствии с законом сохранения энергии в консервативной системе:

При движении пружинного маятника от положения равновесия его потенциальная энергия увеличивается, а кинетическая уменьшается (см. рис. 5.6, а). Когда маятник проходит положение равновесия (? = 0), его потенциальная энергия равна нулю, а кинетическая энергия маятника максимальна и равна полной энергии. В состоянии максимального отклонения от положения равновесия скорость маятника равна нулю, следовательно, равна нулю и кинетическая энергия, а потенциальная — максимальна и равна полной энергии. Следовательно, в момент максимального отклонения и когда маятник проходит положение равновесия имеет место:

Приведенные сведения об энергии колебаний пружинного маятника имеют общее значение и справедливы для свободных гармонических незатухающих колебаний в любой колебательной системе.

Вынужденные колебания — колебания, происходящие под действием внешней, периодически действующей силы.

Вынужденные колебания совершают, например, игла швейной машины, нож электробритвы, поршень в цилиндре двигателя внутреннего сгорания и др.

Вынуждающая сила — сила, вызывающая вынужденные колебания.

Если вынуждающая сила меняется гармонически по закону F = F_maxcos(ot (F_max — амплитуда вынуждающей силы, со — ее циклическая частота), то в колебательной системе, на которую действует эта сила, через определенное время (соответствует переходному режиму) устанавливаются гармонические вынужденные колебания с частотой, равной частоте со вынуждающей силы (рис. 5.8).

Уравнение вынужденных колебаний:

где А — амплитуда вынужденных колебаний; ю — циклическая частота свободных незатухающих колебаний системы; ср — разность фаз между смещением х и вынуждающей силой F. Амплитуда установившихся вынужденных колебаний:

где F_max — амплитуда вынуждающей силы; т — масса колеблющейся системы; со — циклическая частота внешней силы; г —

коэффициент сопротивления; (3 =—коэффициент затуха-

Для вынужденных колебаний характерно явление резонанса.

Разность фаз между смещением и вынуждающей силой:

Резонанс — явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте ш колебаний системы. Соответственно величина а>_рсз называется резонансной циклической частотой, а кривые зависимости А от оз — резонансными кривыми (рис. 5.9).

Резонансная циклическая частота и резонансная амплитуда:

Возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше трение в системе (Р —*? 0). На практике амплитуда А в точке со конечна за счет сопротивления среды (р| > р2 > Ро), поэтому с ростом резонансная частота сдвигается в сторону меньших частот, а резонансная амплитуда — понижается (А_рез1

Читать еще: Уплотнение грунта пневматическими трамбовками как посчитать объем

Кинетическая энергия груза на пружине формула

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих возникшие свободные колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

1) максимальный импульс груза

2) частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Движение пружинного маятника определяется гармоническим законом вида:

Соответственно, изменение скорости груза пружинного маятника, равно:

откуда значение максимальной скорости:

Так как циклическая частота , то максимальная скорость

Формула под буквой А соответствует максимальному импульсу груза

Б) Частота колебания пружинного маятника определяется формулой:

Система тел может обладать как кинетической, так и потенциальной энергией.

Полная механическая энергия тела представляет собой сумму его кинетической и потенциальной энергий:

где W k — кинетическая энергия тела; W p — потенциальная энергия тела.

Полная механическая энергия системы нескольких тел представляет собой сумму полных механических энергий всех тел системы:

E = E 1 + E 2 + . + E N ,

где E 1 — полная механическая энергия первого тела; E 2 — полная механическая энергия второго тела и т.д.

Полная механическая энергия системы нескольких тел является суммой кинетических и потенциальных энергий каждого тела, входящего в данную систему:

где E k — сумма кинетических энергий всех тел системы ( кинетическая энергия системы ); E p — сумма потенциальных энергий всех тел системы ( потенциальная энергия системы ).

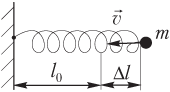
Пример 28. Груз массой 0,50 кг, прикрепленный к пружине жесткостью 0,10 кН/м, совершает колебания в горизонтальной плоскости. Вычислить полную механическую энергию системы пружина — груз в момент времени, когда пружина растянута на 10 см, а закрепленный на ее конце груз имеет скорость 2,0 м/с.

Решение. Полная механическая энергия системы пружина — груз является суммой потенциальной энергии пружины и кинетической энергии груза:

где W p — потенциальная энергия деформированной пружины; W k — кинетическая энергия груза.

На рисунке изображена система пружина — груз, показаны направление скорости движения груза и величина растяжения пружины ∆ l .

Значения потенциальной энергии пружины и кинетической энергии груза определяются формулами:

потенциальная энергия деформированной пружины

W p = k ( Δ l ) 2 2 ;

кинетическая энергия движущегося груза

где k — коэффициент жесткости пружины; ∆ l — величина деформации (растяжения) пружины; m — масса груза; v — величина скорости груза.

Подстановка записанных формул для W p и W k в исходное выражение дает формулу для расчета полной механической энергии системы пружина — груз в указанный момент времени:

E = k ( Δ l ) 2 2 + m v 2 2 .

E = 0 ,10 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 + 0,50 ⋅ 2,0 2 2 = 1,5 Дж.

Пример 29. Тело массой 1,0 кг брошено с поверхности Земли с начальной скоростью 20 м/с под углом 30° к горизонту. Найти полную механическую энергию тела относительно поверхности Земли через 2,0 секунды полета. Сопротивлением воздуха пренебречь.

Решение. Полная механическая энергия тела является суммой потенциальной энергии тела относительно поверхности Земли и его кинетической энергии:

где W k — кинетическая энергия; W p — потенциальная энергия тела.

На рисунке изображена траектория движения тела, показаны направления скорости его движения и выбранная система координат.

Значения потенциальной и кинетической энергии тела определяются формулами:

где m — масса тела; g — модуль ускорения свободного падения; h — высота тела над поверхностью Земли в указанный момент времени; v — модуль скорости тела.

Для расчета кинетической энергии тела необходимо вычислить величину скорости тела в указанный момент времени. Расчет произведем по формуле

v = v x 2 + v y 2 ,

где v x — проекция скорости тела на ось Ox ; v y — проекция скорости тела на ось Oy .

Проекции скорости определяются выражениями

v x = v 0 cos α = 20 cos 30 ° = 10 3 м/с ; v y = v 0 sin α − g t 0 = 20 sin 30 ° − 10 ⋅ 2,0 = − 10 м/с , >

где v 0 — модуль начальной скорости тела; t 0 = 2,0 с — момент времени, в который определяется значение полной энергии тела.

Подстановка полученных значений в выражение для вычисления модуля скорости дает ее значение:

v = ( 10 3 ) 2 + ( − 10 ) 2 = 20 м/с.

Для расчета потенциальной энергии тела необходимо вычислить высоту подъема тела над поверхностью Земли в указанный момент времени:

h = y ( t 0 ) = v 0 t 0 sin 30 ° − g t 0 2 2 = 20 ⋅ 2,0 ⋅ 0,5 − 0,5 ⋅ 10 ⋅ ( 2,0 ) 2 = 0 м,

т.е. в указанный момент времени тело упало на Землю.

Подставим найденные значения скорости и высоты подъема в исходное уравнение для расчета полной энергии и выполним расчет:

E = m g h + m v 2 2 = 1,0 ⋅ 10 ⋅ 0 + 1,0 ⋅ 20 2 2 = 200 Дж = 0,20 кДж.

Нетрудно заметить, что найденное значение полной механической энергии тела в указанный момент времени совпадает со значением полной механической энергии в начальный момент времени:

E 0 = m v 0 2 2 = 1,0 ⋅ 20 2 2 = 200 Дж.

имеет место только в отсутствие сопротивления воздуха.

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Читать еще: В каком году открыли электричество

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени. Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия.

Максимальная кинетическая энергия груза на пружине

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

Для груза на пружине:

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле , а частота как . Циклическая частота , следовательно, для буквы А имеем ответ под номером 2.

Б) Для пружинного маятника известны формулы кинетической энергии и потенциальной энергии . Учитывая, что начальная скорость тела равна 0, то вся потенциальная энергия переходит в кинетическую, то есть . Ответ под номером 3.

Пружинный маятник, состоящий из груза и лёгкой пружины, совершает колебания. В момент, когда груз находится в крайнем положении, его немного подталкивают вдоль оси пружины в направлении от положения

равновесия. Как в результате этого изменяются максимальная кинетическая энергия груза маятника и частота его колебаний?

Для каждой величины определите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Груз подтолкнули от положения равновесия, откуда следует, что амплитуда колебаний груза увеличится. При этом увеличится также и максимальная потенциальная энергия пружины. По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.

Период и частота пружинного маятника зависят только от массы груза и жесткости пружины. Таким образом, при увеличении амплитуды колебаний груза, частота колебаний маятника не изменится.

Формулы пружинного маятника

Определение и формулы пружинного маятника

Пружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.

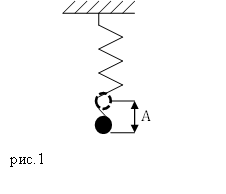
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

где $<�щu>^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

где $_0=sqrt>>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $<(omega >_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde=Releft(Acdot exp left(ileft(_0t+varphi right)right)right)left(3right).]

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

Так как частота колебаний ($nu $) — величина обратная к периоду, то:

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).

Амплитуду можно найти как:

начальная фаза при этом:

где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

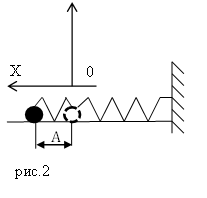
Читать еще: Домкрат подкатной 3 5 тонны ремонт

Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

Закон сохранения энергии для пружинного маятника запишем как:

где $dot=v$ — скорость движения груза; $E_k=frac>^2><2>$ — кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Примеры задач с решением

Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac<�Н><�м>$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac<�м><�с>$?

Решение. Сделаем рисунок.

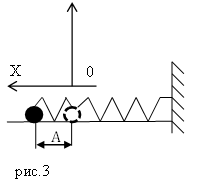
По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:

где $E_$ — потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_$ — кинетическая энергия шарика, в момент прохождения положения равновесия.

Потенциальная энергия равна:

В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем:

Из (1.4) выразим искомую величину:

Вычислим начальное (максимальное) смещение груза от положения равновесия:

Ответ. $x_0=1,5$ мм

Задание. Пружинный маятник совершает колебания по закону: $x=A $где $A$ и $omega $ — постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_$. В какой момент времени это произойдет?

Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:

Потенциальную энергию колебаний груза найдем как:

В момент времени, который следует найти $F=F_0$; $E_p=E_$, значит:

Максимальная кинетическая энергия груза формула

Кинетическая энергия

Кинетическая энергия — внутренняя энергия движущегося тела, обусловленная его инертностью (массой) и скоростью. Она равна энергии, которую нужно затратить, чтобы снизить скорость этого тела до нуля.

Например, движущийся автомобиль невозможно остановить мгновенно. Для остановки необходимо затратить энергию трения тормозных колодок о тормозные диски колес и шин об асфальт.

Кинетическая и потенциальная энергия измеряются в джоулях ($1 Дж = Н cdot м$).

В некоторых физических системах происходят циклические преобразования потенциальной (запасенной) энергии в кинетическую и обратно. Такие системы называются маятниками. Например, для груза, подвешенного на нити, потенциальная энергия максимальна, когда он отклонен на максимальный угол от вертикали. Мгновенная скорость груза в этот момент равна нулю и, следовательно, нулю равна и кинетическая энергия. По мере движения вниз под действием силы тяжести, скорость груза нарастает и достигает максимума в нижней точке, после чего снова начинает запасаться по мере движения вверх.

Попробуй обратиться за помощью к преподавателям

Проще всего изучать переход кинетической и потенциальной энергий друг в друга на примере пружинного маятника, где действует, если пренебречь силой трения, лишь сила упругости. Когда пружину сжимают, энергия запасается. Когда отпускают — потенциальная энергия, сохраненная в кристаллической решетке материала, высвобождается и превращается в кинетическую, разгоняя груз. Когда скорость груза достигает максимума, он продолжает движение по инерции, растягивая пружину в противоположном направлении, вновь запасая энергию и снижая скорость. Характеристики такого колебательного движения зависят только от материала пружины, толщины проволоки, из которой она намотана, диаметра и количества витков. Все эти факторы описываются единым параметром — коэффициентом упругости.

Максимальная кинетическая энергия груза

Для простого пружинного маятника полную энергию груза в любой момент времени можно выразить как

$E_p$ — потенциальная энергия,
$E_k$ — кинетическая энергия,
$m$ — масса,
$v$ — моментальная скорость,
$k$ — коэффициент упругости,
$x$ — приращение длины пружины в данный момент.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Максимальную кинетическую энергию можно вычислить как

где $v_ $ — максимальная скорость груза. Однако измерить ее на практике сложно. Проще, опираясь на постоянство суммы кинетической и потенциальной энергий, определить максимальную потенциальную (когда кинетическая равна нулю). Поскольку справедливо и обратное, можно записать:

где $x_ $ — максимальное приращение растяжения пружины. Его легко измерить, а коэффициент упругости посмотреть в справочнике.

Компактный груз, массой 0,5 кг прикреплен к движущейся горизонтально пружине. Ее коэффициент упругости равен 2000 $frac $. Каково было начальное приращение длины пружины, если его максимальная скорость во время колебаний составляет 1 $frac $?

Из условий задачи можно найти максимальную кинетическую энергию груза:

Выразив максимальную потенциальную энергию через приращение длины пружины, составим равенство:

Ответ: $approx 1,6 мм$.

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Груз математического маятника массой 10 г совершает гармонические колебания. При этом скорость v груза изменяется с течением времени t по закону v = 2sin ( 0,5πt )

Чему равна максимальная кинетическая энергия груза при таких колебаниях?

помогите пожалуйста — вот я знаю Е кин = mv^2/2
но от куда я должна взять значения. что взять из этой формулы? ( v = 2sin ( 0,5πt )) 2 — это скорость, которую можно подставить в Е?
0,5 это w , с этим что то сделать?

оу. не я получила 0,02. Тааак. а в каких это единицах? это равно 2м дж?