Какие поверхности называют линейчатыми

Ответы по начертательной геометрии

1.Какой способ задания поверхности называется кинематическим. Поверхность рассматривается как совокупность всех последовательных положений

некоторой линии – образующей — перемещающейся в пространстве по определенному

закону. Линия, которую пересекают все образующие поверхности, называется

2.Что называется определителем поверхности. Совокупность независимых геометрических элементов однозначно определяющих поверхность в пространстве.

3. из каких частей состоит определитель поверхности. Определитель поверхности состоит из двух частей: Геометрической части — совокупности геометрических фигур, с помощью которых можно образовать поверхность. Алгоритмической части — алгоритма формирования поверхности при помощи фигур, входящих в геометрическую часть определителя. Определитель кривой поверхности Ф может быть записан в символической форме: Ф(Г)[А], где (Г) — геометрическая часть, [А] — алгоритмическая часть. Для каждой поверхности обе части определителя имеют вполне конкретное содержание.

4.Какие сведения содержит геометрическая часть определителя поверхности. Геометрическая часть определителя содержит форму образующей и направляющих; В геометрическую часть определителя входят геометрические фигуры и отношения между ними.

5.Какие сведения содержит алгоритмическая часть определителя поверхности. Алгоритмическая часть определителя поверхности представляет собой алгоритм построения точек и линий поверхности, занимающих на ней переменное положение.

6.Какая поверхность называется линейчатой. Линейчатая поверхность – поверхность образованная движением прямой линии.

7.Какая поверхность называется поверхностью вращения. Это поверхность, образуемая при вращении вокруг неподвижной оси произвольной линии.

8.Что называется параллелью и меридианом поверхности вращения. Меридиан — линия полученная рассечением поверхности вращения плоскостью проходящей через её ось. Параллель — окружность образованная вращением точки вокруг оси.

9.Что называется экватором и горлом поверхности вращения. Горло — самая маленькая параллель, самая большая — экватор.

10.Какие поверхности образуются при вращении прямой линии. цилиндр вращения, если прямая l параллельна оси i;2)конус вращения, если прямая l пересекает ос i; 3)однополостный гиперболоид вращения, если прямая l(ВС) скрещивается с осью i.

11.Какаие поверхности образуются при вращении окружности. 1. Сфера образуется вращением окружности вокруг ее диаметра; 2. Тором называется поверхность, образованная вращением окружности вокруг оси, принадлежащей плоскости окружности, но не проходящей через ее центр. При этом ось вращения может пересекать окружность, касаться ее и располагаться вне окружности. В первых двух случаях тор называется закрытым, в последнем — открытым, или кольцом.

12.Какое перемещение называется винтовым. Винтовое перемещение характеризуется вращением вокруг оси и одновременно поступательным движением, параллельным этой оси. Траектория такого движения – винтовая линия. Поверхность, образованная винтовым движением какой-либо линии, называется винтовой.

13.Какие поверхности называют геликоидами. Поверхность, образованная винтовым движением прямой линии.

14.Какой геликоид называется прямым, а какой косым. Геликоид называется прямым, если образующая перпендикулярно оси винтового движения. Косой геликоид – поверхность, образованная движением прямой линии, скользящей по двум направляющим (одна из них цилиндрическая винтовая линия, а вторая — ось винтовой линии) и сохраняющей во всех положениях постоянный угол с направляющей плоскостью, которую располагают перпендикулярно оси винтовой поверхности.

15.Какой геликоид называется открытым, а какой закрытым. Закрытый геликоид- образующая и ось винтового движения пересекаются; открытый – образующая и ось скрещиваются.

16.Какая поверхность называется трубчатой, а какая циклической. Циклические поверхности, могут быть образованы движением в пространстве какой — либо окружности, постоянного или переменного радиуса при перемещении ее центра по криволинейной направляющей, а плоскость окружности остается перпендикулярной к этой кривой. Трубчатая поверхность образуется движением окружности постоянного радиуса, центр которой 0 перемещается по заданной кривой (направляющей l ), а плоскость окружности остается перпендикулярной этой кривой.

17.Признак принадлежности точки поверхности. Точка принадлежит поверхности, если она принадлежит линии, лежащей в этой поверхности.

18.Как на чертеже задать точку, принадлежащую поверхности. Сначала необходимо построить проекции какой-либо линии, принадлежащей поверхности, затем отметить на этой линии точку.

19.Как на чертеже найти недостающую проекцию точки, принадлежащей поверхности. Провести через точку поверхности линию; по принадлежности линии поверхности найти недостающую проекцию точки.

20.Признак принадлежности линии поверхности. Линия принадлежит поверхности, если все точки этой линии принадлежат поверхности.

21.Простейшие линии на поверхности цилиндра, конуса, сферы, тора. Цилиндр, конус: окружность, прямые. Тор, сфера: окружность.

22.По каким линиям плоскость может пересечь цилиндрическую поверхность вращения. Эллипс, окружность, параллельные прямые

23.В каком случае плоскость пересекает цилиндрическую поверхность вращения по эллипсу. Эллипс, если секущая плоскость наклонена под произвольным углом к оси цилиндра

24.По каким линиям плоскость может пересечь коническую поверхность вращения. Эллипс, окружность, 2 пересекающиеся прямые, парабола, гипербола.

25.В каком случае плоскость пересекает коническую поверхность по образующим. Плоскость проходит через ось вращения.

26.В каком случае плоскость пересекает коническую поверхность по окружности. Секущая плоскость перпендикулярна оси вращения конуса

27.В каком случае плоскость пересекает коническую поверхность по эллипсу. Секущая плоскость пересекает все образующие не параллельно и не перпендикулярно оси.

28.В каком случае плоскость пересекает коническую поверхность по параболе. секущая плоскость параллельна одной из образующих поверхности конуса.

29.Коническую поверхность по гиперболе. секущая плоскость пересекает обе половины поверхности конуса.

30.По каким линиям плоскость пересекает сферу. По окружности.

31. Какие плоскости пересекают открытый тор по окружности. Параллельно оси вращения; перпендикулярно оси вращения – по направляющим.

32.Что называется линией пересечения двух поверхностей. Линией пересечения 2-ух поверхностей называется множество точек общих для данных поверхностей.

33.Из каких точек состоит линия пересечения двух поверхностей. Из множества точек линии пересечения выделяют характерные точки, с которых следует начинать построение этой линии. Они позволяют увидеть, в каких границах можно применить положение вспомогательных секущих поверхностей для определения остальных точек.

34.Общий алгоритм построения точек, принадлежащих линии пересечения двух поверхностей. 1) Анализ условия. Определить типы пересек поверхностей, характерные точки пересечения, кол-во контуров и способы построения точек линии пересечения.

2) Построить опорные точки. К ним относятся точки пересечения очерковых или крайних

образующих одной поверхности с другой. Эти точки будут как правило

экстремальными. Эти же точки определяют грань видимости.

3) Построить доп точки, эти точки выбираются произвольно между характерными для уточнения кривизны линии пресеч.

4) Полученные точки соединить плавной кривой с учетом видимости считая пов-ти пересеч

монолитными и непрозрач

35.Построение линии пересечения двух поверхностей, одна из которых занимает проецирующее положение. Сразу известна одна из проекций линии пересечения. Достраиваем вторую проекцию.

36. В каком случае при построении линии пересечения двух поверхностей используют вспомогательные плоскости. Этот способ применяют лишь в тех случаях, когда вспомогательные плоскости рассекают поверхности по простым линиям – прямым или окружностям, которые проецируются на соответствующую плоскость проекций без искажения

37.В каком случае при построении линии пересечения двух поверхностей используют вспомогательные с постоянным центром(концентрические сферы). : Обе заданные поверхности являются поверхностями вращения; Поверхности имеют общую плоскость симметрии, параллельную одной из плоскостей проекций; Оси заданных поверхностей пересекаются.

38. с переменным центром(эксцентрические сферы). Способ эксцентрических сфер применим для поверхностей несущих на себе семейство окружностей, если поверхности имеют общую плоскость симметрии, параллельную одной из плоскостей проекции.

39.В каких пределах выбирают радиусы вспомогательных сфер при применении способа концентрических сфер. сфера минимального радиуса будет касаться одной из данных поверхностей, а со второй – пересекаться. Радиус максимальной сферы Rmax равен расстоянию от центра вспомогательных сфер до наиболее удаленной точки пересечения очерковых образующих

40.Алгоритм нахождения точек, принадлежащих линии пересечения поверхностей, при использовании способа эксцентрических секущих сфер. 1) Построить экстремальные точки, используя в качестве посредника общ пл-ть симм данных пов-тей; 2) Построение случайных точек с помощью вспомогательных сфер, центры которых принадлежат оси пов-ти вр. Построение с участием каждого посредника выполняется в такой последовательности:

— на цикл пов-ти выбир окр Д, расположенная между построенными ранее экстр точками

— через окр Д провод вспомог сф Г, цетр О которой принадл оси пов-ти вращ

-строятся окр д1, д2 …. По которым посредник Д пересек пов-ть вр

— отмеч точки пересеч окр-тей Д и д1, д21

3) Постр точек видимости лин пересеч

41.Какие точки линии пересечения поверхностей относятся к особенным(характерным) точкам. Это точки, определяющие границы применения вспомогательных секущих сфер. (33)

42.По каким линиям пересекаются соосные поверхности вращения. Две соосные поверхности вращения пересекаются по окружностям число которых равно числу точек пересечения меридианов этих поверхностей.

43.По каким линиям пересекаются цилиндрические поверхности с параллельными образующими.По параллельным прямым

44.По каким линиям пересекаются конические поверхности с общей вершиной. По пересекающимся прямым. (образующим)

45. Теорема Монжа. Если две поверхности второго порядка описаны вокруг третьей или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

46.Что называется точкой пересечения линии и поверхности. Точка, общая для линии и поверхности.

47.Алгоритм решения задачи на построение проекций точки пересечения линии и поверхности в случае проецирующего положения одной из фигур. Мы сразу знаем одну из проекций точки пересечения. По линиям связи переносим на другую проекцию.

48.Общий алгоритм построения точек пересечения линии и поверхности, когда ни одна из фигур не занимает проец. положения. Через данную линию проводим вспомогательную поверхность; строим линию пересечения вспомогательной и данной поверхностей; отмечаем точку пересечения данной и построенной линий — искомая точка.

49.Алгоритм нахождения точек пересечения прямой со сферой. Через данную прямую проводим вспомогательную поверхность; строим окружность, по которой вспомогательная пересечет сферу; отмечаем точки пересечения окружности с данной прямой – искомые точки.

50.В какую плоскость следует заключать прямую для нахождения точек пересеч. ее с цилиндрической поверх. общего положения. В вспомогательную плоскость, проходящую через прямую и параллельную образующим цилиндра.

51. В какую плоскость следует заключать прямую для нахождения точек пересеч. ее с конической. В вспомогательную плоскость, проходящую через прямую и вершину конуса.

52.Какая прямая называется касательной к кривой линии. Касательной к кривой линии называется прямая, представляющая собой предельное положение секущей.

53.Касательная к поверхности. Прямая линия, касательная к какой-либо кривой, принадлежащей поверхности, является касательной к поверхности.

54.Как построить касательную к произвольному меридиану поверхности вращения в заданной точке. Соединить центр меридиана и заданную точку; построить перпендикуляр к построенному отрезку.

55.Какая плоскость называется касательной к поверхности. Касательная плоскость к поверхности есть множество всех касательных, проведенных к поверхности через одну и ту же точку.

56.Каким может быть взаимное положение касательной плоскости и поверхности. Касательная плоскость может иметь с поверхностью одну общую точку и располагаться по одну сторону от нее (такие точки поверхности называются эллиптическими). Касательная плоскость к поверхности в некоторой ее точке может пересекать поверхность по прямым или кривым линиям (гиперболические точки). Касательная плоскость может иметь с поверхностью общую линию – прямую или кривую. (точки кривой поверхности, принадлежащие линии касания, параболические)

57.Как на чертеже построить проекции касательной плоскости. Через данную точку на поверхности проводим две пересекающиеся линии. Строим касательные к этим линия в точке. Эти касательные определяют касательную плоскость.

58.Что называется нормалью к поверхности. Нормалью к поверхности в точке называется перпендикуляр к касательной плоскости в точке касания.

59.Какова последовательность построения нормали к поверхности. Через данную точку на поверхности проводим две пересекающиеся линии. Строим касательные к этим линия в точке. Эти касательные определяют касательную плоскость. Перпендикуляр поставленный к касательной плоскости является нормалью.

60.Как построить проекции нормали в заданной на поверхности вращения точке без построения касательной плоскости. Построить через данную точку фронталь и горизонталь. Нормаль будет перпендикулярна фронтали на пи2 и горизонтали на пи1.

«Формирование поверхностей вращения, линейчатых поверхностей в пространстве и задание их на чертеже»

В чем состоит сущность кинематического способа образования поверхностей?

При кинематическом способе поверхность рассматривается как совокупность всех

последовательных положений некоторой линии (образующей), перемещающейся по определенному закону, задаваемому другой линией (направляющей).

Что такое «определитель поверхности», из чего состоит (его составные части, что он в себя включает)?

Определитель это совокупность условий, позволяющих реализовать закон образования поверхности;

а) геометрическая часть — задаются постоянные геометрические элементы (точка, прямая и т.п.)

б) алгоритмическая часть — дополнительные сведения о характере перемещения образующей (текстовая часть).

Каковы условия принадлежности точки и линии поверхности?

Точка принадлежит поверхности, если она принадлежит линии данной поверхности.

Линия принадлежит поверхности, если все ее точки принадлежат поверхности.

Как образуются линейчатые развертываемые поверхности? Приведите примеры.

Линейчатой поверхностью с вершиной S и направляющей m называют поверхность, образованную движением прямой линии (образующей), которая проходит через вершину S — неподвижную точку в пространстве и пересекает некоторую неподвижную линию m — направляющую.

Различают четыре вида линейчатых поверхностей:

1. Коническая поверхность. Вершина S есть собственная точка пространства, а направляющая m — кривая линия.

2. Цилиндрическая поверхность. Вершина S есть несобственная точка пространства, а направляющая m — кривая линия.

3. Пирамидальная поверхность. Отличается от конической тем, что направляющая m — ломаная линия.

4. Призматическая поверхность. Отличается от цилиндрической тем, что направляющая m — ломаная линия.

Как образуются линейчатые поверхности с плоскостью параллелизма? Назовите их.

При образовании таких поверхностей образующая прямая скользит по направляющим линиям, оставаясь при этом параллельной к некоторой плоскости. Обычно в качестве плоскости параллелизма используется одна из плоскостей проекций.

Разновидности и, соответственно, названия подобных поверхностей определяются формой их направляющих: в виде кривых или прямых линий. Если, к примеру, криволинейные направляющие обозначить и , прямые направляющие — и и плоскость параллелизма как , то будем иметь следующие названия поверхностей: — цилиндроид, — коноид, — косая плоскость или гиперболический параболоид.

Как образуются поверхности вращения? Приведите примеры.

Поверхностью вращения называется поверхность, описываемая кривой (или прямой) линией образующей при ее вращении вокруг неподвижной оси. Эта поверхность определяется на чертеже заданием образующей и оси вращения.

1. Поверхности, образованные вращением прямой линии:

а) цилиндр вращения — поверхность, полученная вращением прямой вокруг её параллельной оси;

б) конус вращения — поверхность, образованная вращением прямой вокруг пересекающейся с ней осью;

в) однополосный гиперболоид вращения — поверхность, полученная вращением прямой вокруг скрещивающейся с ней осью.

2. Поверхности, образованные вращением окружности вокруг неподвижной оси:

а) сфера — поверхность, полученная вращением окружности вокруг ее диаметра;

б) тор — поверхность, полученная вращением окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр.

3. Поверхности вращения, образованные вращением кривых второго порядка:

а) эллипсоид вращения — поверхность, полученная вращением эллипса вокруг оси;

б) параболоид вращения — поверхность, образованная вращением параболы вокруг ее оси.

Какие поверхности называются винтовыми?

Это поверхность, которая образуется винтовым перемещением линии (образующей). Поверхность можно задать начальным положением образующей и направляющей — цилиндрической винтовой линией, которая называется гелисой.

Поверхности, образованные при винтовом движении прямой называются геликоидами. В зависимости от величины угла наклона образующей к оси геликоиды бывают прямыми, если угол равен 90°, и наклонными (косыми), если угол — произвольный, отличный от 0 и 90°.

Прямой геликоид имеет другое название — прямой коноид.

Какие поверхности называют линейчатыми

2.3.3.2. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ.

2.3.3.2.1. Развертывающиеся линейчатые поверхности
2.3.3.2.2. Неразвертывающиеся (косые) линейчатые поверхности

Как уже отмечалось, поверхность называется линейчатой, если она может быть образована перемещением прямой линии. Поверхность, которая не может быть образована движением прямой линии, называется нелинейчатой. Например, конус вращения — линейчатая поверхность, а сфера — нелинейчатая. Через любую точку линейчатой поверхности можно провести, по крайней мере, одну прямую, целиком принадлежащую поверхности. Множество таких прямых представляет собой непрерывный каркас линейчатой поверхности. Линейчатые поверхности разделяются на два вида: 1) развертывающиеся поверхности;
2) неразвертывающиеся, или косые поверхности.
Примечание. Все нелинейчатые поверхности являются неразвертывающимися. Рассмотрим несколько наиболее характерных разновидностей тех и других линейчатых поверхностей.

Поверхность называется развертывающейся, если она путем изгибания может быть совмещена с плоскостью без образования складок и разрывов. Очевидно, что все многогранные поверхности являются развертывающимися. Из кривых поверхностей этим свойством обладают только те линейчатые поверхности, которые имеют ребро возврата.
Существует только три вида линейчатых поверхностей, имеющих ребро возврата: торсы, конические и цилиндрические (Рис. 2.3.19) .

Торсы

1) пространственная ломаная линия 1, 2, 3, 4, 5, б. преобразуется в пространственную кривую линию m;
2) ребра многогранной поверхности преобразуются в касательные к пространственной кривой m;
3) многогранная поверхность преобразуется в линейчатую двухполую развертывающуюся кривую поверхность, которая называется торсом.

Множество всех касательных прямых к пространственной кривой представляет собой непрерывный каркас поверхности торса. Через каждую точку поверхности проходит одна касательная к кривой m. Таким образом, торс представляет собой поверхность, которая образуется непрерывным движением прямолинейной образующей, касающейся во всех своих положениях некоторой пространственной кривой линии. Направляющая пространственная кривая m (рис. 2.3.20, б) служит границей между двумя полостями поверхности торса и называется ребром возврата. Если взять на кривой m какую-либо точку В и провести через нее плоскость , пересекающую обе полости поверхности, то полученная в пересечении кривая АВС будет иметь так называемую точку возврата B. Следовательно, ребро возврата является множеством точек возврата кривых линий, полученных при пересечении данной поверхности различными плоскостями. Этим и объясняется ее название. Если ребром возврата является цилиндрическая винтовая линия, то такая поверхность называется развертывающимся геликоидом. Так как углы наклона всех образующих этой поверхности к плоскости, перпендикулярной оси винтовой линии, одинаковы, она является поверхностью одинакового ската.

Плоскость, перпендикулярная оси поверхности, пересекает ее по эвольвенте окружности. Свойством развертываемости торс обладает потому, что он является пределом некоторой развертывающейся многогранной поверхности. Геометрическая часть определителя торса состоит из ребра возврата. Алгоритмическая часть определителя торса состоит из указания о том, что образующая прямая при своем движении остается касательной к ребру возврата. Если ребро возврата выродится в собственную точку пространства, то образующие торса, проходя через нее, образуют коническую поверхность произвольного вида. Если эта точка (вырожденное ребро возврата) будет несобственной точкой пространства, то образующие торса, проходя через нее, окажутся параллельными между собой и образуют цилиндрическую поверхность общего вида. Таким образом, цилиндрическая и коническая поверхности обладают свойством развертываемости, так как являются частными случаями поверхности торса. Однако, чтобы задать коническую или цилиндрическую поверхности, недостаточно иметь только ребро возврата (собственную или несобственную точку) — положение образующей прямой не определяется одной точкой. Необходимо задать еще направляющую линию.
Рис. 2.3.20, 1 анимация

К вопросу о развертываемости кривой линейчатой поверхности можно подойти и с точки зрения дифференциальной геометрии, которая доказывает, что линейчатая поверхность является развертывающейся, если касательная плоскость, проведенная в какой-либо точке поверхности, касается ее по прямолинейной образующей поверхности, проходящей через эту точку. Таким свойством обладают только три вида поверхностей: торс, коническая и цилиндрическая.
Анимационный рис. 2.3.20. 1 показывает кинематику формирования торса, у которого в качестве направляющей взята винтовая линия. Поверхность образована перемещением прямой по направляющей пространственной кривой ( винтовой линии). В процессе движения в каждый момент времени образующая прямая является касательной к направляющей.

Цилиндрические поверхности

Неподвижная кривая m(m₁ m₂), по которой скользит образующая l(l₁l₂), называется направляющей. Если направляющая линия является кривой второго порядка, то и цилиндрическая поверхность будет второго порядка. Геометрическая часть определителя цилиндрической поверхности состоит из направляющей линии m и исходного положения образующей l (рис. 2.3.21).
Алгоритмическая часть определителя состоит из указания о том, что любая образующая поверхности может быть построена как прямая, пересекающая кривую m и параллельная прямой l. Цилиндрическая поверхность является бесконечной в направлении своих образуюших. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения — его основаниями (рис. 2.3.22, 2.3.23). Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают:
Рис. 2.3.22

1) круговые — нормальное сечение круг (рис. 2.3.22);
2) эллиптические — нормальное сечение эллипс (рис. 2.3.23);
3) параболические — нормальное сечение парабола;
4) гиперболические — нормальное сечение гипербола;
5) общего вида — нормальное сечение кривая случайного вида (рис. 2.3.20). Если за основание цилиндра принимается его нормальное сечение, цилиндр называют прямым (2.3.22, а).
Если за основание цилиндра принимается одно из косых сечений, цилиндр называют наклонным (рис. 2.3.22, б, 2.3.23, б, в).
Наклонные сечения прямого кругового цилиндра являются эллипсами (сечения плоскостями (₂) и ‘(‘ ₂) на рис. 2.3.22, а). На рис. 2.3.22, б изображен наклонный цилиндр, основаниями которого являются косые сечения (эллипсы).
Рис. 2.3.23

Наклонные сечения прямого эллиптического цилиндра в общем случае — эллипсы. Однако его всегда можно пересечь плоскостью, наклонной к его образующим, таким образом, что в сечении получится круг. Эллиптический цилиндр имеет две системы круговых сечений (построение их рассмотрено в гл. 4). На рис. 2.3.23, а показаны плоскости Г(Г₂) и Г'(Г’₂), пересекающие эллиптический цилиндр по окружностям. На рис. 2.3.23, б, в выполнены чертежи наклонных эллиптических цилиндров, основаниями которых являются их круговые сечения.

Конические поверхности

Неподвижная кривая m(m₁,m₂), по которой скользит образующая l(l₁,l₂), называется направляющей. Если направляющая линия является кривой второго порядка, то и коническая поверхность будет второго порядка. Неподвижная точка S(S₁,S₂), делящая поверхность на две бесконечные полы, называется вершиной. Множество прямолинейных образующих представляет собой непрерывный каркас конической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая (исключением является только вершина S, которая называется «особой точкой поверхности». Геометрическая часть определителя конической поверхности состоит из направляющей кривой m и вершины S.
Алгоритмическая часть определителя состоит из указания о том, что любая образующая поверхности может быть построена как прямая, проходящая через вершину S и пересекающая кривую m. Часть замкнутой конической поверхности, ограниченная вершиной и какой-либо плоскостью, пересекающей все ее образующие, называется конусом. Фигура сечения конической поверхности этой плоскостью называется основанием конуса. Сечение конической поверхности плоскостью, перпендикулярной ее оси, называется нормальным. Осью конической поверхности называется линия пересечения ее плоскостей симметрии. Следовательно, не все конические поверхности имеют ось, а только те, которые имеют не меньше двух плоскостей симметрии.
Конические поверхности, не имеющие оси (а следовательно, и нормального сечения), называются коническими поверхностями общего вида.

Конические поверхности, имеющие ось, в зависимости от вида нормального сечения бывают:
1) круговые — нормальное сечение круг (рис. 2.3.25);
2) эллиптические — нормальное сечение эллипс (рис. 2.3.26) и другие.
Если за основание конуса принимается фигура его нормального сечения, конус называют прямым, если иное сечение — наклонным. Прямой круговой конус изображен на рис. 2.3.25, а, наклонный круговой конус — на рис. 2.3.25, б. Основанием такого конуса может быть только эллипс (см. раздел 4), ось его не проходит через центр основания.
Прямой эллиптический конус показан на рис. 2.3.26, а. Эллиптический конус (так же как и эллиптический цилиндр) имеет две системы круговых сечений. Построение круговых сечений поверхностей второго порядка рассматривается в разделе 4.3.

Если принять одно из них за основание конуса, получим наклонный эллиптический конус с круговым основанием (рис. 2.3.26, б). Ось наклонного конуса не проходит через центр основания. Заметим, что у всех развертывающихся линейчатых поверхностей две смежные образующие либо пересекаются (торс, коническая поверхность), либо параллельны (цилиндрическая поверхность).

Линейчатые поверхности. Принадлежность линии и точки к поверхности

Линейчатой называется поверхность, образующей которой является прямая линия.

В общем случае линейчатая поверхность однозначно определяется тремя направляющими линиями [8, стр. 142].

Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этойповерхности. Для задания поверхности достаточно иметь проекции направляющей линии и указать, как строится образующая прямая, проходящая через любую точку направляющей. Однако, для придания наглядности изображения, вычерчивают очерк, линии видимости и строят точки на поверхности.

Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некоторой кривой направляющей линии. Если направляющей линией является окружность, то поверхность называется наклонным или эллиптическим конусом.

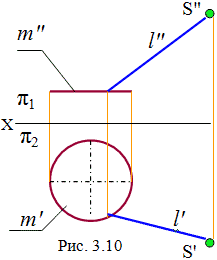
На рис. 3.10 представлены: направляющая окружность – m; неподвижная точка – S; прямолинейная образующая — l . Это первая часть определителя – геометрическая. Образующая движется по направляющей, оставаясь неподвижной в точке S. Описание закона движения является алгоритмической частью определителя. При этих условиях поверхность на чертеже считается заданной. Для придания наглядности, на рис. 3.11 построены очертания поверхности, линии видимости и промежуточная точка, принадлежащая поверхности.

Построение точек, принадлежащих поверхности, осуществляется следующим образом. Пусть задана фронтальная проекция точки А (А»). На фронтальной плоскости она изображена как невидимая. Для построения ее горизонтальной проекции через точку задаем линию, принадлежащую поверхности. Этой линией будет окружность, так как линия задана параллельно основанию, а основанием является окружность. Центр окружности лежит на осевой линии поверхности. Проводим линию связи из центра окружности на горизонтальную плоскость до пересечения с горизонтальной осевой поверхности. Строим окружность, которой принадлежит точка А.. По линии связи отмечаем ее местоположение с учетом видимости для горизонтальной плоскости, где точка является видимой. Аналогичные построения выполняются для наклонного (эллиптического) цилиндра.

Тема 4

Позиционные задачи

Все задачи начертательной геометрии условно могут быть разделены на метрические и позиционные. К метрическим задачам относятся задачи на измерение линейных и угловых величин. Решение этих задач будет рассмотрено ниже.

К позиционным задачам относятся задачи на принадлежность и взаимное пересечение геометрических фигур. По существу решение позиционных задач сводится к нахождению точек одновременно принадлежащих двум или более фигурам. Задачи на определение принадлежности одной геометрической фигуры к другой частично уже рассмотрены:

o принадлежность точки к прямой (рис. 1.23) .

o принадлежность линии к поверхности. Рис. 3.9 ;

o принадлежность точки к поверхности. Рис. 3.11

Задачи на построение линий пересечения геометрических фигур условно можно разделить на три группы:

o пересечение плоскости с поверхностью;

o пересечение прямой линии с плоскостью и с поверхностью.

o взаимное пересечение поверхностей.

Решение всех типов позиционных задач на пересечение подчиняются общему алгоритму. На рис. 4.1 представлена поверхность полусферы и усеченного конуса. Для построения точек, одновременно принадлежащих этим поверхностям, воспользуемся общим алгоритмом.

1. Вводится вспомогательная поверхность, в частном случае — плоскость. Эта вспомогательная поверхность назначается таким образом, чтобы она пересекла обе фигуры по простым для построения линиям — по прямым или по окружностям.

2. Строятся линии пересечения вспомогательной поверхности с каждой из заданных фигур.

3. Отмечаются точки взаимного пересечения построенных линий. Эти точки принадлежат обеим фигурам, следовательно, являются элементом пересечения фигур.

4. Соединяют точки в определенной последовательности и определяют видимость линии пересечения и фигур друг относительно друга.

Находить точки для построения линии взаимного пересечения фигур надо в определенной последовательности.

1. В первую очередь отмечают точки на контурных образующих или на ребрах, если поверхностигранные.

2. Находят экстремальные точки: наивысшую; наинизшую; самую левую; самую правую; самую ближнюю и самую дальнюю.

3. Отмечают точки на линиях среза (принадлежащие основаниям).

4. Если построенных точек недостаточно для выявления формы линии взаимного пересечения, строят ряд промежуточных (случайных) точек.

Лекция 7. Поверхности

7.1. Поверхности. Образование и задание поверхности на чертеже

Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.

Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.

Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).

Поверхность можно рассматривать, как совокупность последовательных положений l₁,l₂… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).

Подвижную линию принято называть образующей (l_i), неподвижные – направляющими (m). Такой способ образования поверхности принято называть кинематическим .

Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.

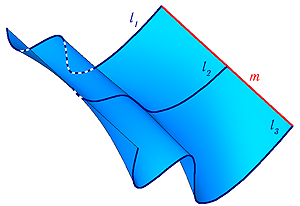
Рисунок 7.1 — Кинематическая поверхность

По виду образующей различают поверхности линейчатые и нелинейчатые , образующая первых – прямая линия, вторых – кривая.

Линейчатые поверхности в свою очередь разделяют на развертывающиеся , которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся .

Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).

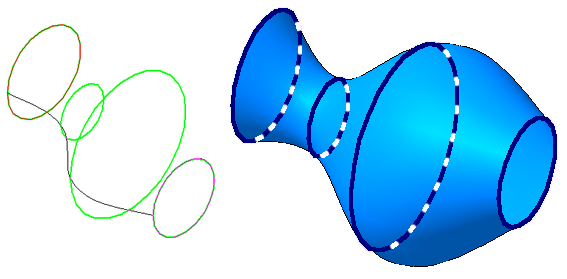
Рисунок 7.2 — Циклическая поверхность

Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:

• поверхности вращения;
• винтовые поверхности;
• поверхности с плоскостью параллелизма;
• поверхности параллельного переноса.

Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).

Для графического изображения поверхности на чертеже используется её каркас.

Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности .

Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом .

Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.

Различают две части определителя: геометрическую и алгоритмическую.

Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.

Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.

Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:

• Геометрическая часть определителя: три направляющих l, m, n.

• Алгоритмическая часть: выбираем плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим восьмиугольник, определяемый тремя найденными точками. Переходим к следующей плоскости и повторяем построение

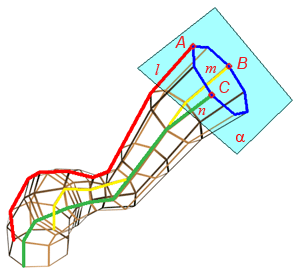
Рисунок 7.3 –Образование циклической поверхности

7.2. Поверхности вращения

Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).

Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.

Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.

Линейчатые поверхности

Одним из объектов трехмерного пространства являются поверхности. Это непрерывное, бесконечное множество точек, которые имеют определенную, строго установленную, зависимость между координатами. Основными инструментами трехмерного моделирования служат различные способы их отражения.

В инженерной графике, начертательной геометрии есть метод, когда поверхность рассматривается как комплекс последовательных расположений линии, которая, подчиняясь определенному закону, перемещается в пространстве. Это кинематический способ, благодаря которому образуются геометрические объекты. Примером выступают технологические процессы, связанные с обработкой материала режущим инструментом. Плоскость получаемого изделия рассматривается как множество линий, эквивалентных (конгруэнтных) форме профиля резца режущего инструмента.

Для описания процесса образования используются два основных термина:

1. Образующая – это подвижная линия. Она, перемещаясь, может иметь постоянную форму. Если это кривая — получается нелинейчатая поверхность. Она относится к I классу. Когда образующая представлена прямой, это ведет к формированию линейчатой поверхности (II класс).
2. Направляющая – это неподвижная линия или плоскость, по ней движется образующая. Однозначно определить рассматриваемый объект возможно тремя линиями, задающими траекторию движения. Но, должно выполняться требование: две из трех линий задаются произвольно, третья – должна быть внутри конгруэнции, которая определяется уже выбранными двумя.

Линейчатые поверхности – понятие, используемое для описания класса тел, которые образуются путем беспрерывного перемещения в пространстве прямой.

Такое перемещение не является хаотичным, оно подчиняется определенному закону. Законом может выступать перемещение вдоль неподвижных линий. Иными словами, образующая все время занимает конкретное установленное положение.

Определены следующие два вида линейчатых поверхностей:

• развертывающаяся;
• неразвертывающаяся (косая).

В пределах класса эти объекты, образованные перемещением прямой линии, подразделяются на:

1. Группы. Классификация на группы зависит от внешних условий движения образующей, то есть от количества направляющих.
2. Виды. Деление на виды по каждой группе определяется внутренними характеристиками движения – формой и относительным положением траекторий, по которым движется прямая.

Их образование может происходить вращением или поступательным передвижением образующей прямой. Цилиндры, конусы – примеры геометрических тел, образованных пересечением линейчатой поверхности вращения с областью, называемой основанием. Гранные объекты формируются поступательным передвижением образующей вдоль ломанных траекторий. Так образуются призмы и пирамиды.

Развертывающиеся поверхности

Эти объекты важны для листопрокатного производства, текстильной промышленности, авиа- и автомобилестроения. Представление о них основывается на допущении, что они обладают гибкостью, но они нерастяжимы и несжимаемы. Под развертывающимися понимают области, которые, изгибая, можно совмещать с плоскостью без порывов, перегибов и складок. Таким образом получается развертка. Это свойство характерно для многогранных объектов и объектов, которые имеют ребра возврата.

Ребро возврата – это направляющая кривая в пространстве, которую касается прямая при передвижении. В системе отсчета развертывающаяся линейчатая поверхность определяется ребром возврата. Указанными характеристиками обладают: торс, а также его частные случаи: объекты, имеющие форму конуса, цилиндра, призмы, пирамиды.

Торсы используются при проектировании деталей и узлов в машиностроении. Образование линейчатых поверхностей, имеющих вид торса, происходит при передвижении образующей, которая во всех позициях проходит по касательной относительно ребра возврата. Оно, совместно с движущейся прямой, определяет торс в пространстве. Этот геометрический объект составляют две полости, граничащие по ребру возврата.

Цилиндрическая

Это особый вид торса. При этом ребро возврата переродилось в несобственную точку, удаленную на бесконечное расстояние. Построенная прямая образующая движется параллельно самой себе по установленной кривой. Чтобы определить цилиндрическую поверхность надо задаться: вектором перемещения и криволинейной траекторией движения.

Коническая

В ней ребро возврата преобразовалось в собственную точку, через которую, по определенной кривой, проходит образующая. Эта точка служит вершиной конуса. Такой объект может складываться из двух полостей. Для его определения задаются указанными точкой и кривой.

Призматическая и пирамидальная

Призматическая отличается от цилиндрической тем, что движение прямой происходит не по кривой траектории, а по ломанной. Ребро возврата преобразовалось в несобственную точку, которая находится на бесконечном расстоянии.

Пирамидальная и конусная различаются формой траектории движения прямой. У конусной — траектория движения криволинейная, у пирамидальной – ломанная.

У перечисленных видов две смежные прямые могут:

• пересекаться (торс, коническая, пирамидальная);
• быть параллельными (цилиндрическая, призматическая).

Чтобы получить уравнение поверхности развертывающейся надо решить систему двух уравнений:

1. уравнения образующей.
2. уравнения направляющей.

Рассмотренные объекты могут быть замкнутыми, если траектория имеет форму окружности или замкнутого многоугольника.

Неразвертывающиеся или косые поверхности

Их возникновение часто обусловлено передвижением прямолинейной образующей вдоль траектории, сформированной тремя направляющими. Они конкретно определяют закон перемещения и бывают прямыми или кривыми. Есть частные случаи, когда траектория движения определяется:

• двумя направляющими и произвольной плоскостью;
• направляющими произвольной формы и плоскостью параллелизма (например, область проекции).

Направляющая плоскость замещает одну из линий траектории. С ней движущаяся прямая составляет постоянный угол.

Если этот угол равен нулю, образующая скользит параллельно направляющей области. Она получила название «плоскость параллелизма». Неразвертывающиеся поверхности, ей определяемые, называются косыми.

Примеры таких объектов: цилиндроид, коноид, гиперболический параболоид. Их основные характеристики приведены в таблице.