Как правильно измерить угол

Транспортир — как правильно пользоваться инструментом для построения и измерения углов?

Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.

Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.

Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.

Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.

В то время предпочтительными материалами для их изготовления были:

В первой половине XX века начали применять олово и целлулоид.

Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».

Разновидности и использование

Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.

Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.

Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.

Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.

Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:

• теодолит;
• оптический транспортир в строительной промышленности и геодезии;
• инклинометр для определения уклонов и косвенной альтиметрии;
• секстант для навигации.

Измерение градусов угла

Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.

Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.

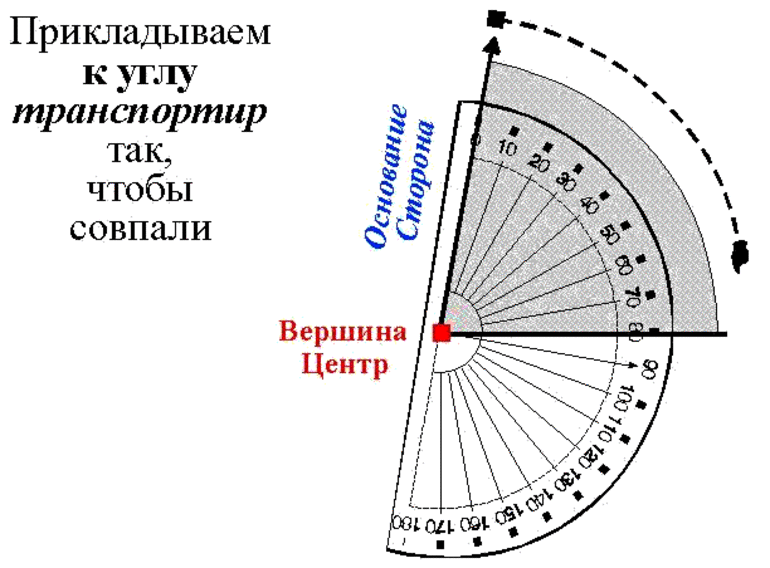
Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.

Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.

Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.

Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.

Построение угла

Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.

Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.

Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.

Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.

Измерение углов. Транспортир

Содержание

Транспортир

Транспортир является самым распространенным инструментом, для того чтобы измерить величину углов. Термин «транспортир», что в переводе с французского обозначает «переносить».

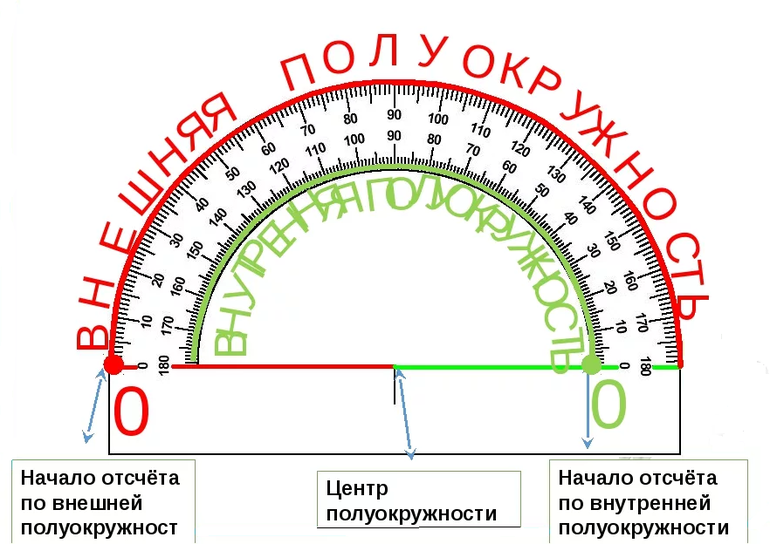
Этот инструмент может иметь разный внешний вид, но у любого транспортира есть шкала, которая расположена на полуокружности. Центр этой шкалы отмечен штрихом или отверстием.

А теперь давайте рассмотрим этот полукруглый предмет и найдем отверстие в центре его плоского угла. Отверстие в транспортире является точкой отсчета и с этой точки начинается линия начала отсчета, которая проходит вдоль всей плоской части транспортира.

Транспортир относится к довольно простому ручному инструменту, с помощью которого можно рисовать и измерять любые углы. Научившись им пользоваться, у вас не будет проблем в решении задач, связанных с измерением углов.

Измерение углов

Измерение углов происходит путем сравнения угла измеряемого с углом, который служит единицей измерения. Для этого нужно внутреннюю часть измеряемого угла постепенно заполнить единичными углами, плотно укладывая один к другому. Количество уложенных углов дает меру угла измеряемого. Самым удобным и распространённым инструментом для измерения углов является транспортир.

В качестве единицы измерения угла может выступать любой угол или другая общепринятая единица измерения.

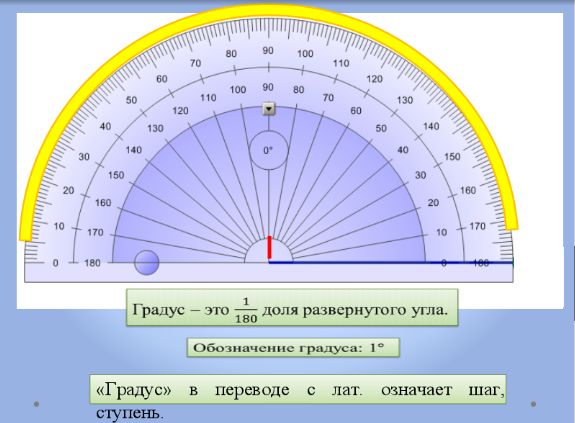
Такой единицей может быть один градус, который составляет 1/180 часть развернутого угла. Поэтому в развернутый угол можно уложить сто восемьдесят углов, равных одному градусу.

Для более наглядного примера берем модель половинки пирога или пиццы, которые разрезаны на сто восемьдесят равных кусочков и плотно уложены один к другому. При этом мы видим, что стороны углов совмещаются со стороной развернутого угла, а дойдя до последней, мы увидим, что она совпадет с другой стороной развернутого угла.

Так на примере картинки в низу, мы видим, что в одну шестую развернутого угла, угол в один градус можно уложить тридцать раз, а в половину развернутого угла – 90 раз.

Если же необходимо измерить угол, который менее одного градуса, то в таких случаях используют другие единицы измерения, например минуты или секунды.

Градусной мерой угла называют положительное число, которое нам показывает то количество раз, которое градус или его части уложились в данном угле.

Но теперь вы уже узнали, что для измерения углов, чаще всего используют такую распространенную единицу измерения, как градус. Его угол равен одной сто восьмидесятой части развернутого угла.

Для удобства измерения углов используют такой чертежный инструмент, как транспортир.

Как измерить угол с помощью транспортира

А сейчас приступим к измерению угла при помощи такого инструмента, как транспортир. Чтобы измерить угол с помощью транспортира, необходимо выполнить несложные действия. Для этого нужно:

• Во-первых, отметить на вершине угла, который вы будете измерять, начальную точку отсчета.
• Во-вторых, нужно совместить нижнюю линию угла с линией, с которой будет осуществляться начало отсчета.
• Далее необходимо отметить на бумаге расположенные цифры, которые бы соответствовали измеряемому углу.
• Следующим вашим шагом будет проведение линии, которая пересекает разметку транспортира. Цифра же, расположенная на месте этого пересечения, указывает на угол в градусах.
• Так как на некоторых транспортирах имеются две противоположно направленные шкалы, то это позволяет измерять углы, которые направлены в разные стороны.

Задание

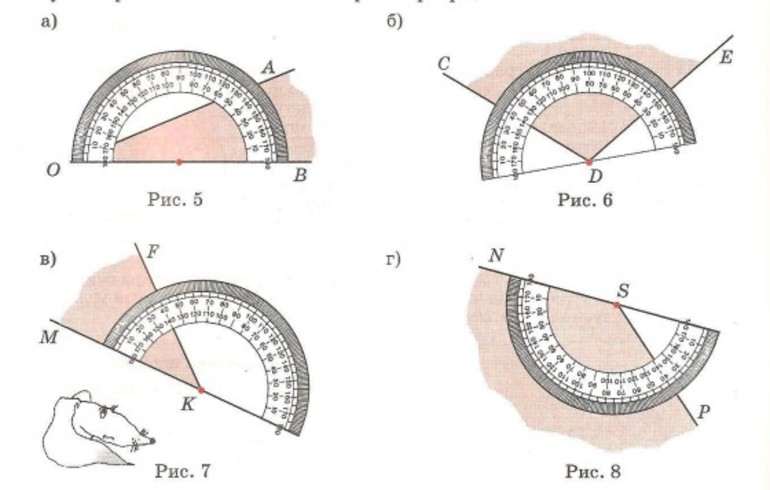
На рисунке вам предоставлены разные виды углов.

1. Какие углы изображены на картинке? Назовите их.

2. С помощью транспортира измерьте приведенные на рисунке углы и запишите их значение:

ий Учебный вопрос: «Способы измерения углов по карте с помощью транспортира и хордоугломера; точность измерения»

Дирекционный угол а (альфа)— это угол между проходящим через данную точку направлением и линией, параллельной оси абсцисс, отсчитываемый от северного направления оси абсцисс по ходу часовой стрелки.

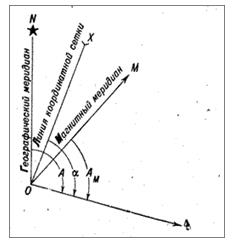
Рис.1 На рисунке а (альфа) — дирекционный угол.

Угол положения 8 (тау) измеряют в обе стороны от направления, принятого за начальное. Прежде чем назвать угол положения объекта (цели), указывают, в какую сторону (вправо, влево) от начального направления он измерен. В морской практике и в некоторых, других случаях направления указывают румбами. Румбом называется угол между северным или южным направлением магнитного меридиана данной точки и определяемым направлением. Величина румба не превышает 90°, поэтому румб сопровождают названием четверти горизонта, к которой направление относится: СВ (северо-восток), СЗ (северо-запад), ЮВ (юго-восток) и ЮЗ (юго-запад). Первая буква показывает направление меридиана, от которого измеряют румб, а вторая — в какую сторону. Например, румб СЗ 52° означает, что данное направление составляет с северным направлением магнитного меридиана угол 52°, который отсчитывается от этого меридиана к западу. Измерение по карте дирекционных углов выполняют транспортиром, артиллерийским кругом или хордоугломером.

Транспортиром дирекционные углы измеряют в таком порядке (рис.2). Исходную точку и местный предмет (цель) соединяют прямой линией, длина которой от точки ее пересечения с вертикальной линией координатной сетки должна быть больше радиуса транспортира. Затем совмещают транспортир с вертикальной линией координатной сетки, сообразуясь с величиной угла. Отсчет по шкале транспортира против прочерченной линии будет соответствовать величине измеряемого дирекционного угла. Средняя ошибка измерения угла транспортиром офицерской линейки составляет 0,5° (0-08).

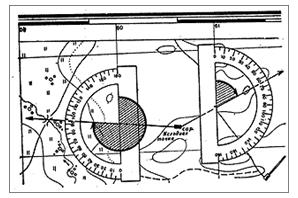
Рис.2 Измерение дирекционного угла транспортиром.

Чтобы провести на карте направление, заданное дирекционным углом в градусной мере, надо через главную точку условного знака исходного пункта провести линию, параллельную вертикальной линии координатной сетки. К линии приложить транспортир и против соответствующего деления шкалы транспортира (отсчета), равного дирекционному углу, поставить точку. После этого через две точки провести прямую линию, которая и будет направлением данного дирекционного угла. Артиллерийским кругом дирекционные углы на карте измеряют так же, как и транспортиром. Центр круга совмещают с исходной точкой, а нулевой радиус — с северным направлением вертикальной линии координатной сетки или параллельной ей прямой. Против прочерченной на карте линии считывают по красной внутренней шкале круга значение измеряемого дирекционного угла в делениях угломера. Средняя ошибка измерений артиллерийским кругом составляет 0-03(10′).

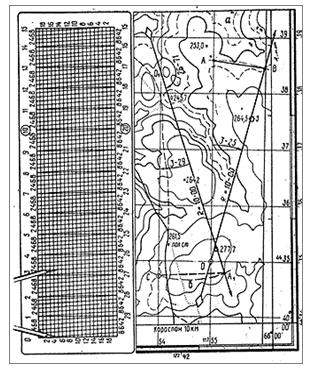
Рис.3 Измерение дирекционного угла с помощью хордоугломера.
а — острый угол;б — тупой угол.

Хордоугломером измеряют углы на карте с помощью циркуля-измерителя. Хордоугломер (рис.3) представляет собой специальный график, выгравированный в виде поперечного масштаба на металлической пластине. В основе его положена зависимость между радиусом окружности R, центральным углом о и длиной хорды а:

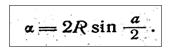
а = sin За единицу принята хорда угла 60° (10-00), длина которой примерно равна радиусу окружности.

На передней горизонтальной шкале хордоугломера через 1-00 нанесены величины хорд, соответствующие углам от 0-00 до 15-00. Малые деления (0-20, 0-40 и т. д:) подписаны цифрами 2, 4, 6, 8. Цифры 2, 4, 6 и т. д. на левой вертикальной шкале обозначают углы В единицах делений угломера (0-02, 0-04, 0-06 и т. д.). Оцифровка делений на нижней горизонтальной и правой вертикальной шкалах предназначена для определения длины хорд при построении дополнительных до 30-00 углов.

Измерение угла с помощью хордоугломера выполняют в таком порядке. Через главные точки условных знаков исходного пункта и местного предмета, на который определяется дирекционный угол, проводят на карте тонкую прямую линию длиной не менее 15см. Из точки пересечений этой линии с вертикальной линией координатной сетки карты циркулемизмерителем делают засечки на линиях, образовавших острый угол, радиусом, равным расстоянию на хордоугломере от 0 до 10 больших делений. Затем измеряют хорду — расстояние между отметками. Не изменяя раствора циркуля-измерителя, левую его иглу передвигают по крайней левой вертикальной линия шкалы хордоугломера до тех пор, пока правая игла не соввадет с каким-либо пересечением наклонной и горизонтальной линий. Левая в правая иглы циркуля-измерителя должны быть всегда на одной и той же горизонтальной линии. В таком положении игл сни-мают отсчет по хордоугломеру.

Если угол меньше 15-00 (90°), то по верхней шкале хордоугломера отсчитывают большие деления и десятки малых делений угломера, а по левой вертикальной шкале — едивицы делений угломера. На рис.3, а хорда АБ соответствует углу 3-25. Если угол больше 15-00, то измеряют дополнение до 30-00, а отсчеты снимают по нижней горизонтальной и правой вертикальной шкалам. Средняя ошибка измерения угла хордоугломером составляет 0-01 — 0-02.

Измерение углов и конусов с помощью угломеров

Угломеры

Для контроля углов у деталей (изделий) в машиностроении широко используют угломеры, угловые призматические меры, уровни, синусные линейки (рисунок 1).

Рис . 1 . Типы угломеров: а – угломер УМ ; б – угломер УН ; в – оптический угломер УО

У угломеров (ГОСТ 5378 – 88) линейка, жестко связанная с нониусом или указателем, может поворачиваться вокруг оси, являющейся одновременно осью угловой шкалы.

1.1 . Угломер с нониусом типа УМ (конструкции Кушникова)

Угломер предназначен для измерения наружных углов в пределах от 0 до 180 0 .

Рис . 2 . Угломер типа УМ : 1 – угольник ; 2 – линейка основания ; 3 – основание ; 4 – сектор ; 5 – устройство для микрометрической подачи ; 6 – нониус ; 7 – стопор ; 8 – подвижная линейка

Метрологические характеристики угломеров УМ

Диапазон измерений, 0

Предел допускаемой погрешности, ‘

Микроподача и стопорение (рисунок 3)

Рис.3. Механизм микроподачи и стопорения: 1 – сектор; 2 – стопор; 3 – винт с правой и левой резьбой; 4 – основание; 5 – зажим микроподачи

Целое число градусов отсчитывается нулевым штрихом нониуса по шкале основания слева направо (рисунок 4)

Рис.4. Пример считывания результата измерения. Целое число градусов равно 31

Построение углового нониуса

Угол между крайними штрихами шкалы нониуса, равный 29 0 , разделен на 30 частей. Угол между соседними штрихами нониуса равен (60’х29):30 = 58′, что на 2′ меньше 1 0 (рисунок 5).

Положение шкал основания и нониуса с величиной отсчета 2′ при нулевом показании

При нулевом показании (когда совпадают нулевые штрихи основания и нониуса) штрих нониуса находится от ближайшего справа штриха основания на расстоянии, равном величине отсчета (2′), умноженной на порядковый номер штриха нониуса, не считая нулевого (рисунок 6).

Рис.6. Порядок определения углов

Определение дробной величины градуса (количество минут) нониусом с величиной отсчета 2′

Дробная величина градуса (34′) получена в результате умножения величины отсчета (2′) на порядковый номер штриха нониуса (17), совпадающего со штрихом основания. Для ускорения чтения показаний используют цифры нониуса: 30’+(2’х2) =34.

При чтении показаний на угломере с нониусом целое число градусов отсчитывают по шкале основания слева направо нулевым штрихом нониуса. Затем находят штрих нониуса, совпадающий со штрихом шкалы основания, и ближайшую к нему слева цифру нониуса. К этой цифре прибавляют результат умножения величины отсчета на порядковый номер совпадающего штриха нониуса, считая его от найденной цифры нониуса (рисунок 7 ).

Рис.7. Определение дробной величины градуса

Измерение острых углов

Для установки и измерения углов от 0 до 90° угломер соединен с угольником (рисунок 8).

Рис.8. Измерение острых углов

Измерение тупых углов

Для установки и измерения углов от 90 до 180° угломер применяют без угольника и к его показаниям прибавляют 90° (рисунок 9).

Рис.9. Измерение тупых углов

Проверка нулевого положения угломера

Перед применением угломер следует протереть. При отсутствии просвета между измерительными поверхностями угломера (или лекального угольника и угломера) нулевые штрихи нониуса и основания должны совпадать (рисунок 10).

Рис.10. проверка нулевого положения угломера

Установка размера. Закрепление микроподачи

После приблизительной установки размера правой рукой закрепляют микроподачу (рисунок 11).

Рис.11. Закрепление микроподачи

Точная установка размера

Сектор относительно основания перемещают также правой рукой (рисунок 12).

Рис.12. Точная установка размера

После установки размера левой рукой закрепляют винт стопора (рисунок 13).

Рис.13. Стопорение шкалы

Установка угломера относительно незакрепленной измеряемой детали

Прижимая слегка правой рукой деталь к измерительной поверхности линейки основания, перемещают ее, уменьшая просвет между деталью и второй измерительной поверхностью угломера до полного их соприкосновения.

После того как угломер установлен относительно детали, проверяют равномерность просвета между измерительными и проверяемыми поверхностями или его отсутствие (при малой шероховатости измерительных и проверяемых поверхностей), фиксируют положение стопором и читают показание (рисунок 14).

Рис.14. Примеры установки угломера относительно незакрепленной измеряемой детали

При чтении показаний угломер следует держать прямо перед глазами

Измерение закрепленной детали (рисунок 15)

Рис.15.Измерение закрепленной детали

После применения угломер надо протереть, смазать антикоррозионным составом, ослабить зажимы и уложить в футляр.

1.2 . Угломер с нониусом типа УН (конструкции Семенова)

Угломер предназначен для измерения наружных углов от 0 до 180 0 и внутренних углов от 40 до 180 0 .

Рис.16. Общее устройство угломера типа УН: 1 – основание; 2 – угольник; 3 – нониус; 4 – стопор; 5 – сектор; 6 – линейка основания; 7 – съемная линейка; 8 – державка

Метрологические характеристики угломера УН

Диапазон измерений, 0

Предел допускаемой погрешности,’

Микроподача и стопорение

Сектор с нониусом плавно перемещают по дуге основания при помощи реечной передачи (рисунок 17). Положение угломера фиксируют стопором (рисунок 18)

Рис.17. Устройство реечной передачи: 1 – основание, 2 – рейка, 3 – сектор, 4 – реечное зубчатое колесо

Рис.18 . Устройство стопора: 1 – сухарь; 2 – основание; 3 – зажимная гайка, 4 – сектор

Построение шкалы основания и нониуса

У угломера типа УН угол между крайними штрихами нониуса равен 29° и разделен на 30 частей, но он построен на дуге большего радиуса, чем у угломера типа УМ, следовательно, расстояние между штрихами больше, что облегчает чтение показаний (рисунок 19).

Правая и левая части шкалы основания рассматриваются от его нулевого штриха.

Рис.19. Построение шкалы основания и нониуса

Основные положения угломера типа УН и чтение показаний

При измерении наружных углов от 0 °до 50° показания читают по правой части шкалы (рисунок 20).

Рис.20. Считывание показаний при измерении наружных углов от 0°до 50°

При измерении наружных углов от 50°до 90° показания читают по левой части шкалы (рисунок 21).

Рис.21. Считывание показаний при измерении наружных углов от 50°до 90°

При измерении наружных углов от 90°до 140° к показаниям правой части шкалы прибавляют 90°(рисунок 22).

Рис.22. Считывание показаний при измерении наружных углов от 90°до 140°

При измерении наружных углов от 140 до 180° к показаниям левой части шкалы прибавляют 90° (рисунок 23).

Рис.23. Считывание показаний при измерении на ружных углов от 140°до 180°

При измерении внутренних углов от 180 до 130° показание правой части шкалы вычитают из 180° (рисунок 24).

Рис.24. Считывание показаний при измерении внутренних углов от 180°до 130°.

При измерении внутренних углов от 130 до 90° показания левой части шкалы вычитают из 180° (рисунок 25).

Рис. 25. Считывание показаний при измерении внутренних углов от 130°до 90 °

При измерении внутренних углов от 90 до 40° показания правой части шкалы вычитают из 90° (рисунок 26).

Рис.26. Считывание показаний при измерении внутренних углов от 90°до 40 °

Проверка нулевого положения угломера

Перед применением угломер следует протереть. При отсутствии просвета между измерительными поверхностями нулевые штрихи нониуса и основания должны совпадать (рисунок 27).

Рис.27. Проверка нулевого положения

Установка угломера относительно наружного угла незакрепленной детали при помощи микроподачи (рисунок 28)

Рис.28. Установка угломера относительно наружного угла незакрепленной детали при помощи микроподачи

При менение микроподачи и стопора при установке размеров (рисунок 29)

Рис. 29. Применение микроподачи и стопора при установке размеров

Установка угломера относительно внутреннего угла незакрепленной детали при помощи микроподачи (рисунок 30)

Рис.30. Установка угломера относительно внутреннего угла незакрепленной детали при помощи микроподачи

Измерение незакрепленной детали без применения микроподачи (рисунок 31)

Рис.31. Измерение незакрепленной детали без применения микроподачи

Измерение закрепленной детали

Линейку основания накладывают на поверхность детали и правой рукой при помощи микроподачи доводят вторую измерительную поверхность угломера до полного соприкосновения с поверхностью детали, являющейся второй образующей проверяемого угла (рисунок 32).

Рис.32.Измерение закрепленной детали

2. Угломер универсальный оптический УО т3-5

Угломер универсальный оптический УО т3-5 (рисунок 33) с нониусом предназначен для измерения наружных и внутренних углов, переднего и заднего углов многолезвийного инструмента с прямолинейными и спиральными зубьями, с равномерным шагом от 5 до 75 мм и с прямолинейным участком по передней и задней граням не менее 1 мм.

Рис.33. Общее устройство угломера оптического: 1 – основание; 2 – шкала — лимб; 3 – крышка; 4 – нониус с линзой; 5 – микровинт; 6 – линейка со скосом

Метрологические характеристики угломеров УО

Диапазон измерений, 0

Предел допускаемой погрешности, ‘

Угломер ( см. рисунок 33 ) смонтирован на круговом основании 1 жестко скрепленным с круговой шкалой — лимбом 2. По дуге основания с помощью рычажка с зубчатой передачей вращается крышка 3, несущая нониус 4 и стеклянную линзу, позволяющую точнее снять отсчет показания прибора. Крышка крепится к основанию с помощью винта, который позволяет закрепить одну из двух прилагаемых линеек с пазами, в которые входит шпонка. К основанию угломера с помощью двух винтов, расположенных с интервалом 22 мм прикреплена пластина с выдержанным зазором 3 мм между пластинами. В зазор между этими двумя винтами с помощью микровинта 5 присоединяется одна (жестко фиксируемая) из двух измерительных баз угломера, выполненная в виде небольшой линейки со скосом 6.

Перед началом работы проверить правильность установки угломера, а именно, совпадение нулевого штриха нониуса с нулевым штрихом шкалы основания, а также последнего штриха нониуса со штрихом шкалы основания, при этом рабочее ребро линейки должно совпасть с рабочей плоскостью измерительной линейки без видимого зазора.

Измерение углов, размеров их сторон, всевозможных сложных контуров, уступов и выемок осуществлять путем различных комбинаций отдельных измерительных звеньев угломера. Сменные линейки, прилагающиеся к угломеру, имеют различные углы скосов на концах, что позволяет выбрать наиболее удобную схему измерения.

Измерение производится контактным методом. При измерении внутренних углов угломер установить на угол, дополняющий измеряемый внутренний угол до 360°. Пример: для измерения угла в 57° 34′ угломер необходимо установить на угол 360°- 57°30′, т.е. на угол 302*30′. Отсчет показаний производится по основной шкале 0 — 360 ̊ с ценой деления 1 ̊ и по нониусному устройству с ценой деления 5′.

Точная установка при измерении углов обеспечивается микрометрической подачей, путем вращения гайки с накаткой, расположенной с тыльной стороны угломера. Фиксирование осуществляется стопорным устройством.

Рис.34 . Измерение углов от 0 до 90°, когда стороны проверяемых углов прикасаются к нижним измерительным поверхностям сдвоенной и сменной линеек

Рис.35. Измерение углов от 0 до 90°, когда стороны проверяемых углов прикасаются к верхней измерительной поверхности сдвоенной линейки и нижней измерительной поверхности сменной линейки

Рис.36. Измерение углов от 90 до 180°, когда стороны проверяемых углов прикасаются к нижним измерительным поверхностям сдвоенной и сменной линеек

Рисунок 37. Измерение угла при вершине конической поверхности

Рисунок 38. Измерение угла детали, одной из образующихся которого является цилиндрическая поверхность

В нашем интернет-магазине вы можете купить угломеры по очень доступным ценам. Для вас мы подобрали наиболее качественные, функциональные и доступные по цене угломеры.

Урок математики по теме «Измерение углов. Транспортир». 5-й класс

Класс: 5

Презентация к уроку

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

• Образовательные:
  • познакомить учащихся с единицей измерения углов, с прибором для измерения углов;
  • научить пользоваться транспортиром.
• Развивающие:
  • развивать внимание, мышление учащихся;
  • развивать самостоятельность учащихся, используя проблемные ситуации, творческие задания;
  • развивать познавательный интерес к предмету.
• Воспитательные:
  • воспитывать чувство взаимоуважения;
  • воспитывать у учащихся навыки учебного труда.

I. Организационный момент

II. Вступительное слово учителя

Мы познакомимся с измерительным прибором (как он называется, вы узнаете немного позже), научимся с его помощью измерять, а затем и строить углы. Вы покажите свои знания, докажите насколько внимательны.
Будем учиться не только математике, но и умению общаться, уважению друг к другу.
Для того чтобы достичь наших целей, вы должны быть волевыми, настойчивыми, целеустремленными, поэтому эпиграфом нашего урока будут слова:

III. Устная работа

Какие из углов, изображенных на рисунке, являются:

а) острыми;
б) тупыми;
в) есть ли среди этих углов прямые?

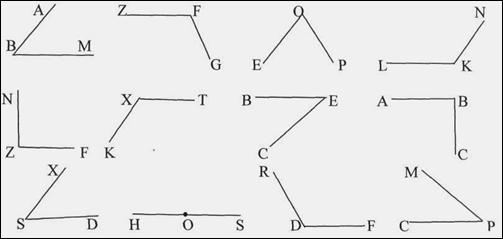
О каком угле мы с вами еще не вспомнили? [О развернутом]
Какой угол называется развернутым? Острым? Прямым? Тупым?

Мы знаем, что два угла можно сравнивать друг с другом.
Какой способ для этого мы использовали? [Наложение]

Но углы, также как и отрезки, можно сравнивать не только наложением, но и с помощью измерения.

IV. Изучение нового материала

Для построения и измерения углов используют специальный прибор. Как он называется, вы узнаете, отгадав кроссворд.

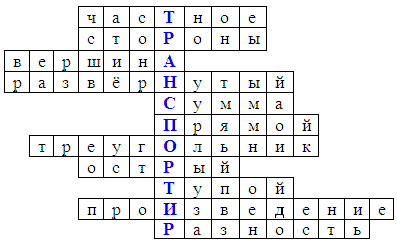
1. Результат деления.
2. Лучи образующие угол.
3. Точка, из которой выходят лучи образующие угол.
4. Угол, который образуют два дополнительных друг другу луча.
5. Результат сложения.
6. Угол, который составляет половину развернутого угла.
7. Инструмент, который используют для построения прямого угла.
8. Угол, меньше прямого.
9. Угол, больше прямого, но меньше развернутого.
10. Результат умножения.
11. Результат вычитания.

Учитель демонстрирует учащимся транспортир или показывает на плакате:

– Для измерения углов применяют транспортир. Положите перед собой транспортиры. Вы видите, какие они разные, но у всех есть нечто общее, о чем мы сейчас будем говорить.

Слайд 5. Итак, шкала транспортира. Она расположена на полуокружности и пронумерована
от 0 до 180. Бывают шкалы двойные: нумерация идет слева направо и справа налево.

Слайд 6. Также есть круглые транспортиры, шкала идет по кругу от 0 до 360, но она также разделена на две полуокружности.

Центр этой полуокружности отмечен на транспортире точкой или черточкой. Найдите на своем транспортире центр и покажите его.

Штрихи шкалы транспортира делят полуокружность на 180 равных частей. Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен 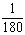доле развернутого угла. Такие углы называют градусами.

Слайд 7. Итак, градусом называют 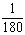долю развернутого угла. Градусы обозначают знаком °. Каждое деление шкалы транспортира равно 1°.

Историческая справка

Слово «градус» – латинское, означает «шаг», «ступень». Измерение углов в градусах появилось более 3 тыс. лет назад в Вавилоне. В расчетах там использовались шестидесятеричная система счисления, шестидесятеричные дроби.
С этим связано, что вавилонские математики и астрономы, а вслед за ними греческие и индийские, полный оборот (окружность) делили на 360 частей – градусов (шесть раз по шестьдесят), каждый градус – на 60 минут, а минуту – на 60 секунд:

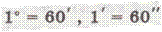
Объяснение учителя (с демонстрацией на доске), как с помощью транспортира можно измерить угол.

– Как измеряют углы с помощью транспортира?

1) Нужно вершину угла совместить с центром транспортира.
2) Одна сторона угла должна проходить через нулевую отметку (0° по шкале).
3) Вторая сторона угла должна пересекать шкалу. Нужно посмотреть, через какую
отметку проходит вторая сторона угла. Это и есть величина этого угла.

Если у транспортира есть две шкалы, то надо смотреть на отметку той шкалы, через ноль которой проходит одна из сторон угла.

V. Практическая работа

Каждому ученику выдается набор углов: острый, прямой, тупой и развернутый.

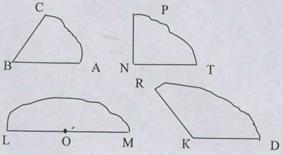
Задания

• Выберите из предложенных вам углов острый, тупой, прямой, развернутый.
• Измерьте их градусную меру и запишите в тетрадях эти данные.
• Сделайте вывод о градусной мере:

а) развернутого угла;
б) прямого угла;
в) острого угла;
г) тупого угла.

Вывод:

VI. Физкультурная пауза

• Покажите руками угол 90°, 180°.
• Покажите руками острый угол, тупой угол.
• Покажите рукой, где вокруг нас есть прямые углы.
• Повернитесь на 180°. А теперь на 90°.

Задание: Начертите в тетради угол любой величины. Предложите соседу по парте его измерить.

VII. Работа по карточкам

У всех учеников карточки с одинаковым заданием.

Задание: Измерьте углы и запишите результаты измерений в тетрадях.

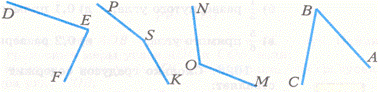
Задание: Выполняется устно с использованием модели часов.

Какой угол образуют часовая и минутная стрелки часов:

а) в 3 ч; в) в 10 ч; д) в 2 ч 30 мин;
б) в 5 ч; г) в 6 ч; е) в 5 ч 30 мин?

Задача №1652

Луч ОС лежит внутри угла АОВ, причем 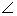АОС = 37°, 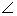ВОС = 19°?.

Измерение углов. Транспортир

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На уроке мы вспомним, что такое единицы измерения, узнаем какими единицами можно измерять углы, познакомимся с такой единицей измерения, как градус, научимся измерять углы в градусах и чертить их с помощью транспортира. Также мы узнаем о других единицах измерения углов, которые применяются в различных ситуациях.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение» и «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур»

Введение

Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.

Метр, дюйм, аршин – это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд – это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.

Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах – время.

В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.

Градусы

Разделим полный угол на 360 равных частей. Для этого удобно использовать окружность. Поделим ее на 360 частей и соединим каждое полученное деление с центром. Получим 360 равных углов (см. Рис. 1).

Рис. 1. Окружность, разделенная на 360 равных углов

Один такой маленький угол назовем углом в 1° (см. Рис. 2).

Не важно, какого размера будет окружность, которую мы делим. Поделим обе окружности на 360 частей, получим равные углы в 1°, хотя стороны одного угла визуально длиннее, чем у другого (см. Рис. 3).

Рис. 3. Углы равны

Стороны углов можно продолжать бесконечно, от этого размер угла не меняется (см. Рис. 4).

Рис. 4. Более явный пример равенства углов

Полный, развернутый, прямой угол

Величина любого угла – это сколько раз в него умещается угол в 1°.

Вот мы видим угол 13° (см. Рис. 5).

Понятно, что полный угол состоит из 360 таких углов. То есть он равен 360° (см. Рис. 6).

Рис. 6. Полный угол

Развернутый угол – это половина полного угла. Он равен (см. Рис. 7).

Рис. 7. Развернутый угол

Прямой угол является половиной развернутого и равен 90° (см. Рис. 8).

Рис. 8. Прямой угол

Эталон градуса нет нужды где-то хранить. Если нужно, то всегда можно полный угол разделить на 360 частей, или развернутый – на 180, или прямой – на 90.

Транспортир

Линейка нужна для того, чтобы измерить имеющийся отрезок или начертить отрезок нужной длины. Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).

Рис. 9. Транспортир

Единицы измерения на ней – градусы. Шкала начинается с нуля и заканчивается 180°.То есть максимальный угол, который мы можем измерить или начертить, – это 180°, развернутый.

Транспортиры могут быть разных размеров, но это не влияет на то, какого размера углы ими измеряют. Для более крупного транспортира у углов нужно чертить стороны длиннее.

Примеры

1. Измерим пару углов.

Прямая часть транспортира совмещается с одной стороной угла, центр транспортира с вершиной угла. Смотрим, где оказалась вторая сторона угла, – 54° (см. Рис. 10, 11).

Рис. 10. Измерение угла

Проделаем то же самое со вторым углом, 137°.

Рис. 11. Измерение угла

Если сторона угла не достает до шкалы, то ее нужно сначала продлить.

2. Начертим углы 29°, 81° и 140°.

Сначала чертим одну сторону угла по линейке (см. Рис. 12).

Рис. 12. Построение одной стороны угла

Отмечаем вершину. Совмещаем с транспортиром. Отмечаем точкой нужное значение угла – 29° (см. Рис. 13).

Рис. 13. Использование транспортира для построения углов

Убираем транспортир. Соединяем полученную точку с вершиной (см. Рис. 14).

Точно так же строим два других угла (см. Рис. 15).

Рис. 15. Построение углов

Заключение

Итак, мы с вами обсудили, что для измерения углов люди договорились использовать градусы. Градус – это полного угла.

Инструментом для измерения и построения углов является транспортир.

Можно не использовать названия углов – полный, развернутый, прямой. Мы можем просто говорить – 360 градусов, 180 или 90 градусов.

Измерение величин «Чужими единицами»

На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.

Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину – скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода – 5 км/ч, 5 минут – это часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.

Точно по такому же принципу устроена другая единица измерения расстояния – световой год. Световой год – расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.

Очень распространенный пример использования «чужой» единицы измерения – это измерять вес в килограммах. На самом деле килограмм – единица измерения массы, а вес – это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.

Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).

Хотя для угла есть свои «родные» единицы измерения – градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол , то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.

Получим величину угла , которая называется тангенсом.

Если увеличить треугольник, то ничего не изменится (см. Рис. 16).

Ведь во сколько раз увеличилась одна сторона, во столько и вторая.

То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.

Другие единицы измерения углов

Существуют и другие единицы измерения углов.

Как и метр можно делить на дециметры, сантиметры, миллиметры для более точных измерений, так и градусы делятся на более мелкие единицы измерения.

Если угол в 1° разделить на 60 равных частей, то величина полученного угла называется минута, 1′.

Если минуту поделить на 60 частей, то полученная величина называется секундой. Секунда – уже очень маленькая величина, но ее тоже можно делить дальше.

Почему вообще стали делить на 360 частей полный угол, ведь это не очень удобно? В древнем Вавилоне была шестидесятеричная система (у нас десятеричная). Им было удобно делить на 60.

Чтобы сделать измерение углов ближе к нашей десятичной системе счисления, были предложены грады. Для этого прямой угол делится на 100 частей. Полученная величина называется град. Полный угол составляет тогда 400 градов. Система не прижилась, и сейчас ее не используют.

Если взять два радиуса окружности так, чтобы кусочек окружности между ними тоже был равен радиусу, то угол между радиусами мы и примем за новую единицу измерения. Он называется 1 рад (радиан). Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).

Например, теперь полный угол (вся окружность) состоит не из целого числа единичных углов. Полный угол состоит из 6 с лишним единичных углов. Не очень удобно, зато теперь длина дуги (части окружности) и угол хорошо связаны. Если взять окружность радиуса 1 см, то величина угла совпадает с длиной дуги. Угол 1 рад – дуга 1 см, угол 2 рад – длина дуги 2 см.

Список литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013.
2. Виленкин Н.Я. и др. Математика. 5 кл. – М.: Мнемозина, 2013.
3. Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. – М.: Мнемозина, 2013.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013. Стр. 144 № 522.
2. Начертите углы: 23°, 167°, 84°.
3. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд.) – 2010. Стр. 163 № 3.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.