Как начертить зубья шестерни

Техническое черчение

Popular

Основы черчения

Строительное

Машиностроительное

Эвольвентный профиль зубца. Построение эвольвенты в общем виде было рассмотрено в главе „Геометрическое черчение». Рассмотрим прак­тическое применение этой кривой при вычерчивании профиля зубцов зубчатых колёс. Пусть даны два цилиндрических зубчатых колеса с модулем m=18 и числом зубцов: первого z₁ = 18, второго z₂ = 12.

Для вычерчивания профиля зубцов пользуемся ранее приведёнными формулами. Находим размеры элементов зубцов.

d₁ = m • z₁ = 18 • 18 = 324 мм; D_e1 = m (z₁ + 2) = 18(18 + 2) = 360 мм;

D_i1= D_e1 — 2 • 2,2 m = 360 — 2 • 2,2 • 18 = 280,8 мм; t= ? • m = 3,14 • 18 = 56,52 мм.

d₂ = m • z₂ = 18 • 12 = 216 мм; D_e2 = m (z₂ + 2) = 18 (12 + 2) = 252 мм;

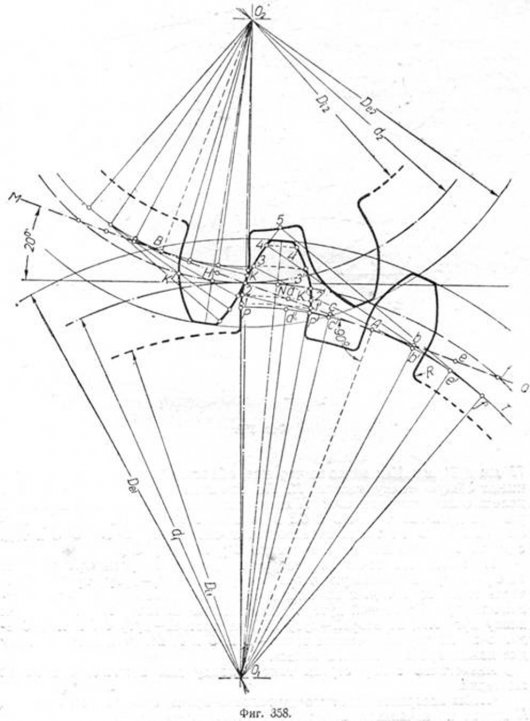
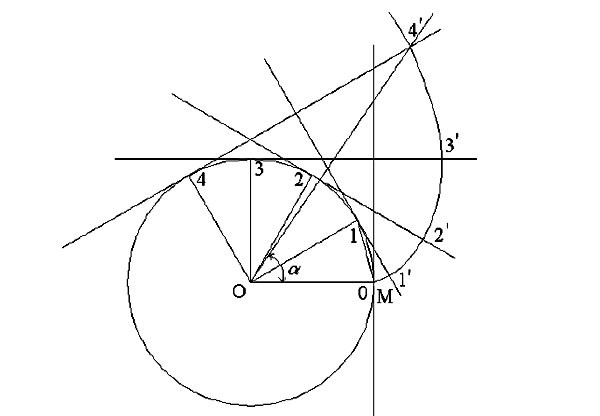
Проводим из центров O₁ и 0₂ (фиг. 358) начальные окружности, окружности выступов и окружности впадин, обращая при этом внимание на то, чтобы начальные окружности обоих колёс имели одну общую точку касания К, лежащую на линии центров O₁—O₂. Далее через точку К проводим под углом 20° к общей касательной начальных окружностей прямую MQ и, опустив из центров О₁ и 0₂ на эту прямую перпендикуляры, получим точки А и В. Из центра О₁ радиусом О₁А описываем основную окружность (на чертеже показана только часть её). Делим прямую KA на равное число частей, например на три, и отметим точки деления буквами d, с и вправо от точки А —b, e, f.

Затем откладываем от точки А влево и вправо эти отрезки по дуге основной окружности PAT; точки деления обозначаем буквами d’, с’, b’, е’_у f ‘ и соединяем их радиусами с центром О₁.

Проводим через точки d’, c’, b’, e’, f’ перпендикулярно к радиусам лучи. Далее на этих лучах откладываем отрезки: на луче d’—отрезок AC, получим точку 1; на луче с’—отрезок Ad, получим точку 2 и т. д. Соединив по лекалу найденные таким образом точки 1, 2, 3, 4, 5, получим эвольвенту, по которой должен быть вычерчен профиль зубца большего колеса.

Аналогичным построением получим профиль зубца и для второго колеса.

Чтобы вычертить полный профиль зубца, откладываем по дугам начальных окружностей от точки К вправо и влево размер толщины зубца s = KK’. Делим s пополам и через середины зубцов, отмеченные точками N и H, проводим прямые O₁N и 0₂H, а затем из центра 0₁ описываем ряд дуг: 1-1′; 2—2′; 3—3′ и т. д. Эти дуги делятся прямой 0₁N пополам. Проводя таким образом дуги из центра 0₂, легко построим полный профиль зубца и для второго колеса. Следует заметить, что по эвольвенте вычерчивается часть зубца—кривая PK5, которая начинается от точки Я, лежащей на основной окружности. Нижняя часть зубца вычерчивается по прямой, имеющей направление от точки P к центру O₁. Место примыкания ножки зубца к окружности впадин скругляется радиу­сом R = 0,2 m. В нашем примере R = 3,6 мм.

Циклоидальный профиль зубца. Образование профиля зубца колеса производится по кривым—эпициклоиде и гипоциклоиде.

Пусть дано: модуль m = 16, число зубцов первого колеса z₁ = 12, второго — z₂ = 8. Для построения зубцов цилиндрических колёс опреде­лим сначала их конструктивные элементы.

Диаметры начальных окружностей

Диаметры окружностей выступов

D_e1 = m (z₁+ 2) = 224 мм; D_e2 = m (z₂ + 2) == 160 мм. Диаметры окружностей впадин

s = 0,487 *t = 24,47 мм,
Строим из центров OI и ОII(фиг. 359) начальные окружности, окружности выступов и впадин. Из точек 01 й 02 описываем вспомогательные окружности, диаметры которых соответственно равны 0,4 d1 и 0,4 d2 т. е.

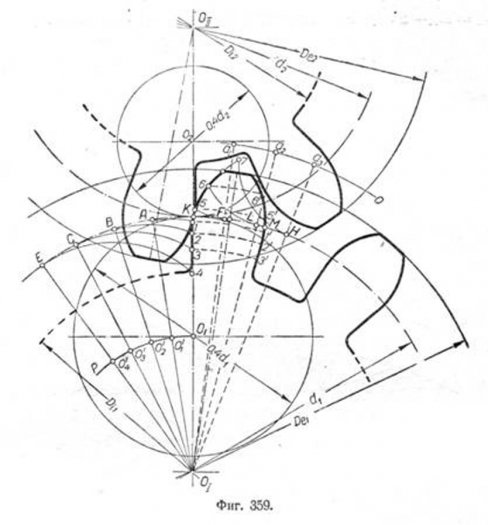
77 мм и 51 мм. Как видно из чертежа, обе вспомогательные окружности имеют общую точку касания К. По начальной окружности большого колеса откладываем от точки К влево равные по величине произвольного размера дуги KA, AB, ВС и СЕ и из центра 0_I радиусом 0_I —О₁ опи­сываем дугу О_I Р. Точки пересечения лучей 0_IA, О_IВ, 0_IС и т.д. с дугой О₁Р отмечаем соответственно 0′₁ 0′₂, 0′₃, 0′₄.

Принимая эти точки за центры, проводим радиусом О₁К ряд дуг: из O₁‘—дугу, проходящую через точку Л, из 0’₂ — дугу, проходящую через точку В, и т. д. и на этих дугах откладываем длины соответст­вующих дуг. На первой дуге, проходящей через точку A, откладываем длину дуги AK, на второй—дугу BK, на третьей—дугу CK и т. д. Сое­динив по лекалу полученные точки—1, 2, 3 и 4, получим гипоциклоиду для ножки зубца большого колеса.

Аналогично этому строим гипоциклоиду для ножки зубца малой шестерни.

Чтобы построить эпициклоиду головки зубца, откладываем от точки К вправо по начальной окружности этого колеса несколько равных по величине произвольного размера дуг KF, FL, LH и проводим из центра O_I радиусом 0_I—0₂ дугу 0₂Q. Пересечения лучей 0_I, F, 0₁ L u O_IH дадут на проведённой дуге точки a₁, а₂ и а₃. Принимая эти точки за центры, проводим радиусом O₂K из точки а₁ дугу, проходящую через точку F.

из а₂—дугу через L и т.д. Отложив затем на первой дуге длину дуги FK, получим точку 5, на второй дуге—длину дуги LK, получим точку 6 и т. д. Соединив точки К, 5, 6 и 7 по лекалу до пересечения с окруж­ностью выступов большего колеса, получим эпициклоиду головки.

Чтобы построить полный профиль этого зубца, необходимо по начальной окружности большего колеса отложить толщину зубца s = 24 мм, равную КМ, разделить её пополам (на чертеже середина отмечена штрих-пунктирной линией, выходящей из O_I ) и затем симмет­рично построить, справа от этой линии, точки 3′, 2′, 1′, 5′, 6′ и т. д.

Построение профиля головки зубца малого колеса производится аналогично построению зубца большего. Для вычерчивания остальных зубцов следует разделить начальные окружности на равное число частей, соответственно числу зубцов шестерни. Расстояние между центрами каждых двух смежных зубцов по дуге начальной окружности должно равняться шагу зацепления t.

Упрощённый способ вычерчивания профиля зубца. Этот способ применяется для вычерчивания эвольвентного профиля зубцов зубчатых

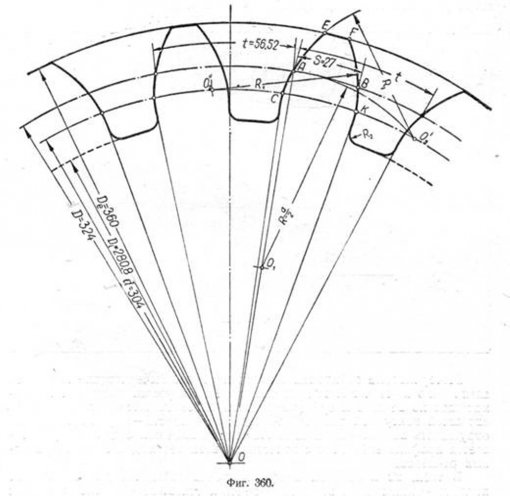
колёс с литыми зубцами, а также для указания обработки, размеров элементов зубца на рабочем чертеже зубчатого колеса и т. п. Рассмотрим это построение на примере.

Пусть даны: d = 324 мм, D_e = 360 мм, D_i=280,8 мм, m=18, z=18, шаг t=56,52 мм и s=27мм; требуется вычертить про­филь зубца (фиг. 360). Из центра 0 зубчатого колеса проводим дуги окружностей диаметров d, D_e и D_i . Определяем диаметр ос­новной окружности по формуле: D = d cos 20° = 324-0,94 = 304 мм и строим её. Намечаем на начальной окружности произвольную точку А и откладываем толщину зубца s = 27 мм = АВ. Соединяем точку А с центром 0 и, разделив OA пополам, получим центр O₁ Радиусом R, рав­ным OA/2 = d/2 из центра О₁ описываем дугу до пересечения с основной ок­ружностью в точке 0₂. Из этой

точки радиусом R₁ проводим дугу CAE, Сделав из точки В на основной окружности засечку тем же радиусом R₁ получим точку 0₂«, из которой описываем дугу ВК. Точки САЕFВК при­надлежат очертанию головки зубца. Ножка зубца строится по прямым линиям, имеющим направление от точек А и В к центру О. Сопряже­ние линий профиля ножки с окружностью впадин выполняется радиу­сом R₂, равным 0,2 m. Профиль остальных зубцов строится аналогичным способом. Откладываем по начальной окружности шаг t и толщину зубца s, затем радиусом R₁ строим головку зубца и т. д.

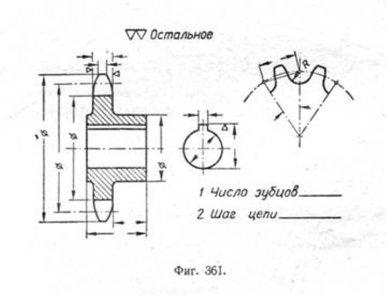
Вычерчивание звёздочек цепных передач. Вычерчивание звёздочек аналогично вычерчиванию зубчатых колёс. Наружная окружность, про­ходящая по вершинам зубьев звёздочки, вычерчивается на главном виде сплошной контурной линией, начальная окружность-штрих-пунктирной, окружность впадин—штриховой. На том же виде или отдельно вычерчи­вается профиль звёздочки с нанесением всех необходимых конструктив­ных размеров.

В табл. 22 приведены профили зубьев звёздочек для приводных втулочно-роликовых и втулочных цепей и основные зависимости для их построения.

В табл. 23 приведены данные для звёздочек зубчатых цепей. На фиг. 361 дан конструктивный чертёж звёздочки для втулочно-роликовой цепи.

Уроки по SolidWorks

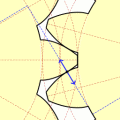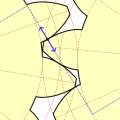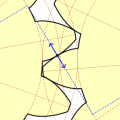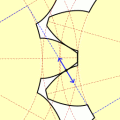Урок посвящен построению зубчатого колеса с эвольвентным профилем зуба. Урок состоит из двух частей. В первой части выложена теория, формулы для расчета и один из способов графического построения эвольвентного профиля зуба.
Во второй части (видео) показан способ построения модели зубчатого колеса с использованием графических построений в первой части урока.

Часто задаваемые вопросы:

*Что такое эвольвента (эволюта)?
*Как построить эвольвенту?
*Как построить зубчатое колесо в программе SolidWorks?
*Формулы для расчета зубчатого колеса?
*Как нарисовать эвольвентный профиль зуба зубчатого колеса?

Итак, начнем с теории.

Эвольвентное зацепление позволяет передавать движение с постоянным передаточным отношением. Эвольвентное зацепление — зубчатое зацепление, в котором профили зубьев очерчены по эвольвенте окружности.
Для этого необходимо чтобы зубья зубчатых колёс были очерчены по кривой, у которой общая нормаль, проведённая через точку касания профилей зубьев, всегда проходит через одну и туже точку на линии, соединяющей центры зубчатых колёс, называемую полюсом зацепления.

Параметры зубчатых колёс

Основной теореме зацепления удовлетворяют различные кривые, в том числе эвольвента и окружность, по которым чаще всего изготавливают профили зубьев зубчатого колеса.

В случае, если профиль зуба выполнен по эвольвенте, передача называется эвольвентной.

Для передачи больших усилий с помощью зубчатых механизмов используют зацепление Новикова, в котором профиль зуба выполнен по окружности.

Окружности, которые катятся в зацеплении без скольжения друг по другу, называются начальными (D).

Окружности, огибающие головки зубьев зубчатых колёс, называются окружностями головок (d₁).

Окружности, огибающие ножки зубьев зубчатых колёс, называются окружностями ножек (d₂).

Окружности, по которым катятся прямые, образующие эвольвенты зубьев первого и второго колёс, называются основными окружностями.

Окружность, которая делит зуб на головку и ножку, называется делительной окружностью (D).

Для нулевых (некорригированных) колёс начальная и делительная окружности совпадают.

Расстояние между одноимёнными точками двух соседних профилей зубьев зубчатого колеса называется шагом по соответствующей окружности.

Шаг можно определить по любой из пяти окружностей. Чаще всего используют делительный шаг p =2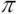r/z, где z – число зубьев зубчатого колеса. Чтобы уйти от иррациональности в расчётах параметров зубчатых колёс, в рассмотрение вводят модуль, измеряемый в миллиметрах, равный

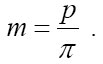
Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности (D) к числу зубьев z или отношению шага p к числу «пи» .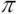

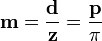
Модуль зубчатого колеса стандартизованы, что является основой для стандартизации других параметров зубчатых колёс.

Основные формулы для расчета эвольвентного зацепления:

Исходными данными для расчета как эвольвенты, так и зубчатого колеса являются следующие параметры: m — Модуль — часть диаметра делительной окружности приходящаяся на один зуб. Модуль — стандартная величина и определяется по справочникам. z — количество зубьев колеса. ? («альфа») — угол профиля исходного контура. Угол является величиной стандартной и равной 20°.

Делительный диаметр рассчитывается по формуле:

Диаметр вершин зубьев рассчитывается по формуле:

d₁=D+2m

Диаметр впадин зубьев рассчитывается по формуле:

d₂=D-2*(c+m)

где с — радиальный зазор пары исходных контуров. Он определяется по формуле:

с = 0,25m

Диаметр основной окружности, развертка которой и будет составлять эвольвенту, определяется по формуле:

d₃ = cos ? * D

От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.

Скачать Скачать с зеркала

Итак, приступим к графическому построению профиля зубчатого колеса.

1. Изобразите делительный диаметр с диаметром D, и центром шестерни O. Окружность показана красным цветом.
2. Изобразите диаметр вершин зубьев (d₁) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета).
3. Изобразите диаметр впадин зубьев (d2) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета цвета).

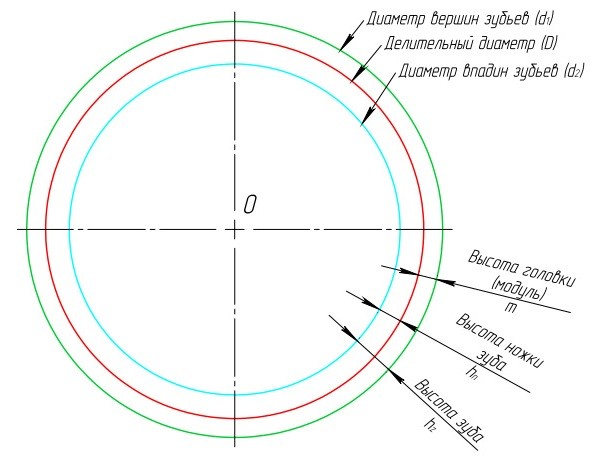
1. Проведите касательную к делительному диаметру (желтая).
2. В точке касания под углом ? проведите линию зацепления, оранжевого цвета.
3. Изобразите окружность касательную к линии зацепления, и центром в точке O. Эта окружность является основной и показана тёмно синего цвета.

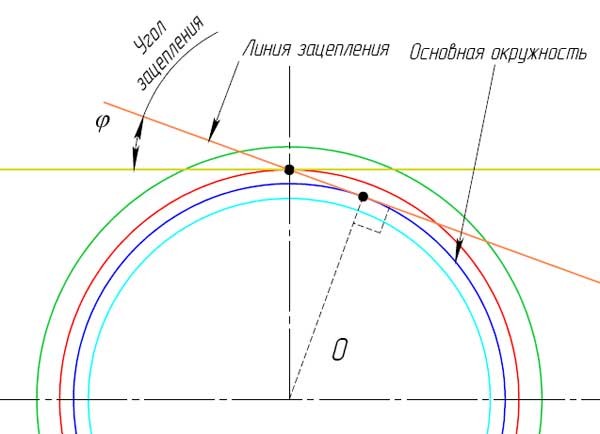
1. Отметьте точку A на диаметре вершин зубьев.
2. На прямой соединяющие точки A и O отметьте точку B находящуюся на основной окружности.
3. Разделите расстояние AB на 3 части и отметьте, точкой C, полученное значение от точки A в сторону точки B на отрезке AB.

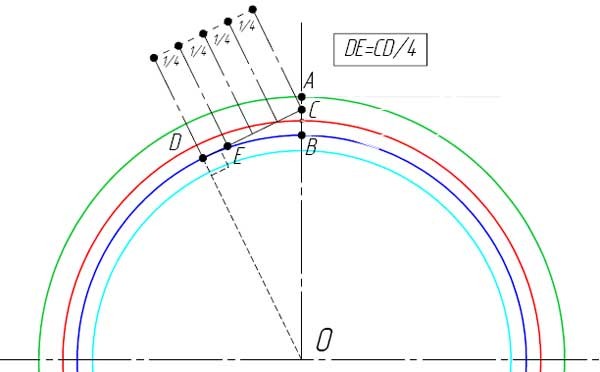
1. От точки C проведите касательную к основной окружности.
2. В точке касания отметьте точку D.
3. Разделите расстояние DC на четыре части и отметьте, точкой E, полученное значение от точки D в сторону точки C на отрезке DC.

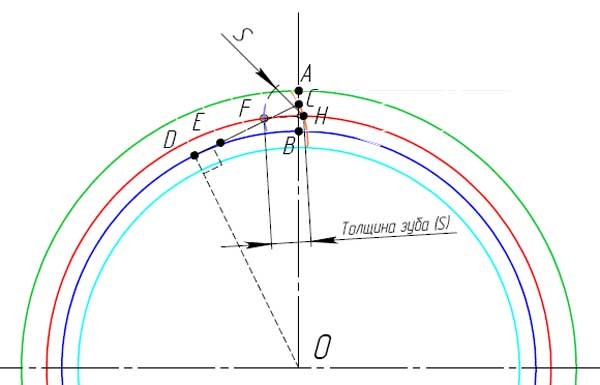
1. Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба, показана оранжевым.
2. Изобразите дугу окружности с центром в точке H, радиусом, равным толщине зуба (s). Место пересечения с делительным диаметром отметьте точкой F. Эта точка находится на другой стороне зуба.

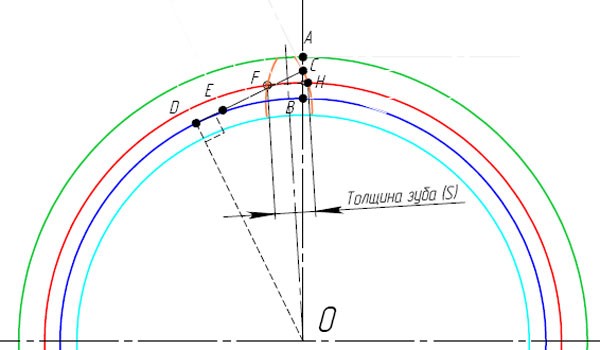
1. Изобразите ось симметрии проходящую через центр О и середину расстояния FH.
2. Линия профиля зуба отображенная зеркально относительно этой оси и будет второй стороной зуба.

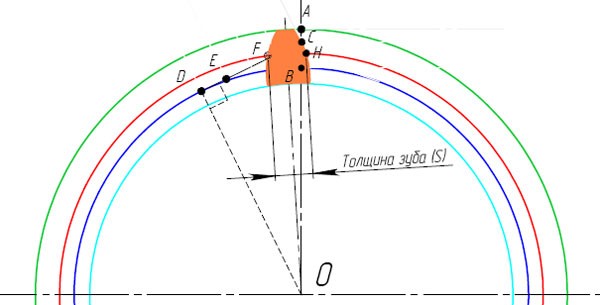
Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:

1. Модуль m=5 мм
2. Число зубьев z=20
3. Угол профиля исходного контура ?=20 0

1. Делительный диаметр D=100 мм
2. Диаметр вершин зубьевd₁=110 мм
3. Диаметр впадин зубьевd₂=87.5 мм
4. Толщина зубьев по делительной окружности S=7.853975 мм

На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой («зубчатые колеса и зубчатые зацепления», а также «динамические сопряжения в SolidWorks») необходимо вместе с изучением этого урока изучать урок №24.

Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.

P.S.(16.03.2010) Скачать Camnetics GearTrax

А теперь переходим с следующей части урока.

Скачать 2-ю часть урока №30 Скачать с зеркала

Как начертить зубья шестерни

Мы используем ONLYOFFICE для работы с заказчиками!

Демовход:
login -rost14@ya.ru
pass — demopass

В чем выгода для меня?

Расчет и построение эвольвенты, сопряжение и анимация пары шестерен (зубчатая передача)

Автор: Рубин Денис Олегович
Источник: www.solidworld.ru
Добавлено: 2013-02-28 06:26:53

В данной статье рассмотрим как правильно рассчитать зубчатое колесо и построить зубчатую передачу из пары шестерен. Это необходимо при проектировании любого типа шестерен и редукторов. В первую очередь необходимо произвести правильное построение профиля зуба при эвольвентном зацеплении, произведя расчет основных параметров по известным формулам. Зубья с эвольвентным профилем определяют параметры, которые характеризуют положение любой точки эвольвенты. В свою очередь эвольвента представляет собой развертку основной окружности диаметром Db в виде траектории точки прямой, которая перекатывается без скольжения по данной окружности (Рисунок 1).

Рисунок 1

Начальными данными для расчета эвольвенты и зубчатого колеса являются:
m — модуль (это часть диаметра делительной окружности, которая приходится на один зуб. Модуль определяется по справочникам, так как является стандартной величиной);
z — количество зубьев;
φ — угол профиля исходного контура. Угол равен 20° (является стандартной величиной).
Для расчета воспользуемся следующими данными:
m = 4; z = 20; φ = 20°.
Делительный диаметр — это диаметр стандартного угла, модуля и шага профиля. Он определяется по формуле:
D = m•z =4•20= 80 мм.
Рассчитаем кривые, которые ограничивают эвольвенту – диаметр впадин зубьев и диаметр вершин зубьев.
Диаметр впадин зубьев рассчитывается по формуле:
Dd = D — 2•(c + m) = 80 — 2•(1 + 3) = 72 мм,
где с – это радиальный зазор пары исходных контуров (с = 0,25•m = 0,25•4 = 1).
Диаметр вершин зубьев рассчитывается по формуле:
Da = D + 2•m = 80 + (2•4) = 88 мм.
Диаметр основной окружности, развертка которой и будет составлять эвольвенту, рассчитывается по формуле:
Db = cos φ • D = cos 20° • 80 = 75,175 мм.
Эвольвента ограничивается диаметрами впадин зубьев и вершин зубьев. Для построения полного профиля зуба нужно рассчитать толщину зуба по делительной окружности:
S = m•((π/2)+(2•х•tg φ)) = 4•((3,14/2) + (2•0•tg 20°)) ≈ 6,284 мм.
где х -коэффициент смещения зубчатого колеса, который выбирается из конструктивных соображений (в нашем случае х = 0).

Далее переходим от расчётных действий к практическим. Создадим эскиз, на котором изобразим вспомогательные окружности с диаметрами рассчитанными ранее (делительная, вершин зубьев, впадин зубьев и основную) (Рисунок 2).

Рисунок 2

Далее установим точку на вспомогательной осевой линии на расстоянии от окружности вершин зубьев равным:
(Da — Dd)/3 = (88-72)/3 = 5,33 мм (или 41,333 от центра оси)
Из данной точки к основной окружности проводим касательную. Для этого соединяем первую установленную точку вспомогательной линией с периметром основной окружности, выделяем окружность и проведенную линию и устанавливаем взаимосвязь «Касательный». На касательной устанавливаем вторую точку на расстоянии от места касания равном четвертой части отрезка, соединяющего первую точку и место касания (в нашем случае это – 17,194 / 4 ≈ 4,299 мм) (Рисунок 3).

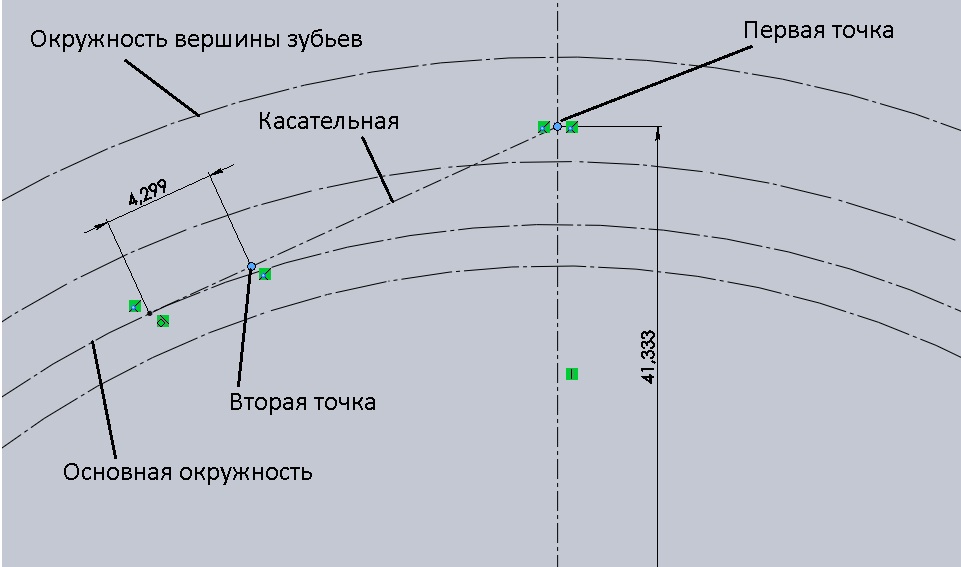
Рисунок 3

Далее с помощью инструмента «Центр дуги» необходимо изобразить дугу окружности в центре второй поставленной точки, которая проходит через первую поставленную точку. Это получится одна сторона зуба (Рисунок 4).

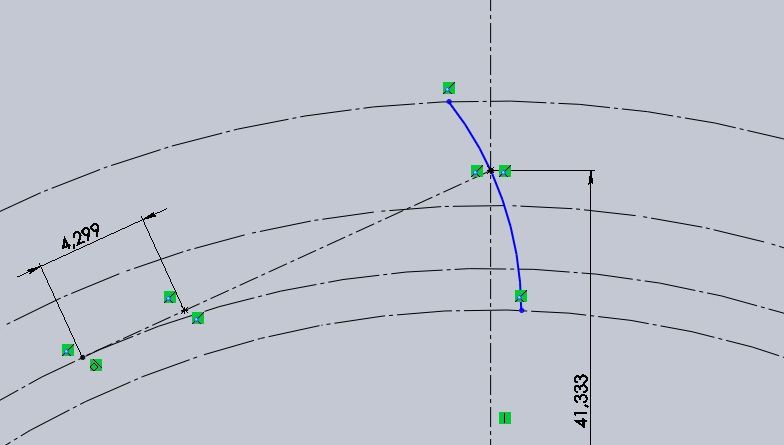
Рисунок 4

Теперь необходимо нарисовать вторую сторону зуба. Для начала проведем вспомогательную линию, соединяющую точки пересечения сторон зуба и делительной окружности, которая по длине равна толщине зуба – 6,284 мм. После этого через середину данной вспомогательной линии и центр оси проведем осевую линию, относительно которой зеркально отобразим вторую сторону зуба (Рисунок 5).

Рисунок 5

Далее дорисовываем верхнюю и нижнюю грань профиля зуба и вытягиваем бобышку. В итоге получается готовый зуб шестерни (Рисунок 6).

Рисунок 6

С помощью инструмента «Ось» вкладки «Справочная геометрия» создаем ось относительно нижней грани зуба (Рисунок 7).

Рисунок 7

С помощью инструмента «круговой массив» («Вставка» / «Массив/Зеркало» / «Круговой массив») размножаем зубья до 20 штук, согласно расчета. Далее рисуем эскиз окружности на фронтальной плоскости зуба и выдавливаем до поверхности. Также сделаем отверстие под вал. В итоге получилось зубчатое колесо с заданными расчетными параметрами (Рисунок 8).

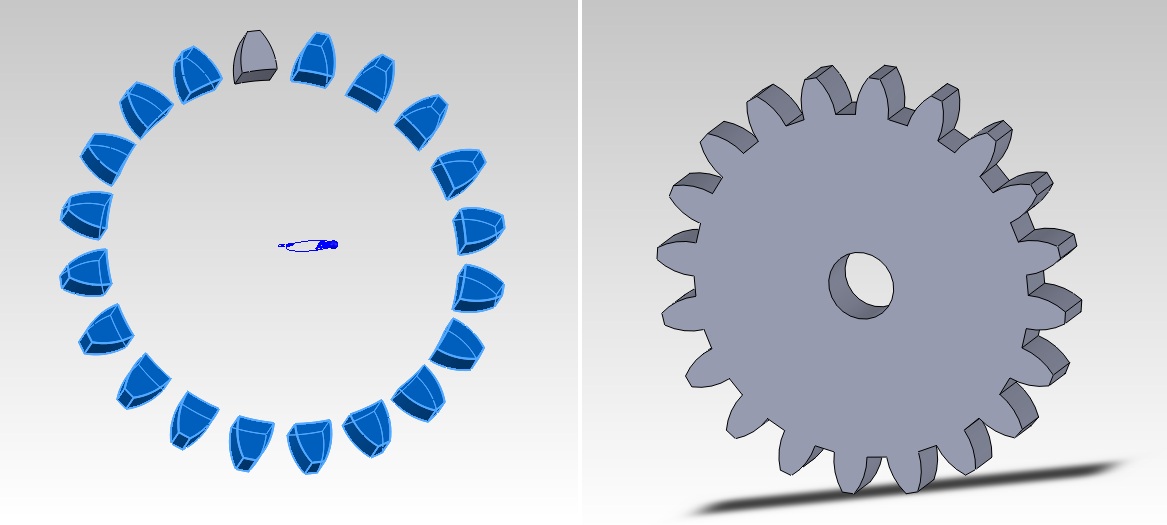
Рисунок 8

Аналогично первому создаем второе зубчатое колесо, но уже с другими расчетными параметрами.
Следующим этапом рассмотрим, как правильно установить взаимосвязи двух зубчатых колес, применяя их в качестве редуктора. Можно воспользоваться созданными моделями зубчатых колес, но еще один способ – это воспользоваться уже имеющейся библиотекой Solidworks Toolbox, где есть много широко используемых компонентов в различных стандартах. Если еще эта библиотека не добавлена, то ее нужно добавить – «Инструменты/Добавления», в выпадающем окне поставить галочки напротив Solidworks Toolbox и Solidworks Toolbox Browser (Рисунок 9).

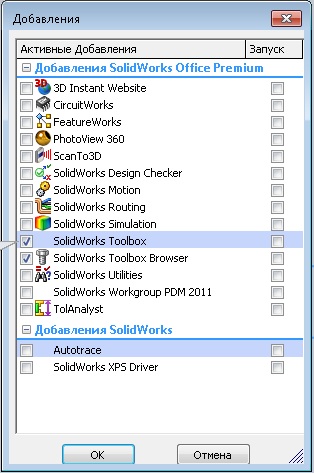
Рисунок 9

Далее создаем сборку, в которую добавляем основание с двумя валами и два зубчатых колеса из библиотеки Toolbox. Для каждого из зубчатых колес выставляем свои параметры. Для этого вызываем меню щелкая по детали правой клавишей мыши, выбираем «Редактировать определение Toolbox» и в окне редактора изменяем параметры (модуль, количество зубьев, диаметр вала и др.). Установим для одного зубчатого колеса количество зубьев 20, а для второго – 30. Остальные параметры оставим без изменений. Для того чтобы правильно сопрячь два зубчатых колеса необходимо чтобы их делительные диаметры были касательны. Делительный диаметр первого зубчатого колеса равен D1 = m•z =4•20= 80 мм, а второго – D2 = m•z =4•30= 120 мм. Соответственно отсюда находим расстояние между центрами – (D1 + D2)/2 = (80 + 120)/ 2 = 100 мм (Рисунок 10).

Рисунок 10

Теперь необходимо выставить положение зубчатых колес. Для этого устанавливаем середину вершины зубьев одного колеса и середину впадин зубьев второго колеса на одной линии (Рисунок 11).

Рисунок 11

Выставленным зубчатым колесам необходимо придать сопряжение. Для этого нажимаем на инструмент «Условия сопряжения», открываем вкладку «Механические сопряжения», выбираем сопряжение «Редуктор». Выбираем две произвольных грани на зубчатых колесах и в пропорциях указываем делительные диаметры, рассчитанные выше (80 мм и 120 мм) (Рисунок 12).

Рисунок 12

Для создания анимации вращения пары зубчатых колес заходим во вкладку «Исследование движения», выбираем инструмент «Двигатель». В открытой слева вкладке выбираем: тип двигателя – вращающийся, местоположение двигателя – шестерня, скорость вращения – например 10 об/мин. Теперь нажимаем на кнопку «Рассчитать» и «Воспроизведение», предварительно выбрав «Тип исследования движения» – Базовое движение. Теперь можно посмотреть движении передачу из двух шестерен, а также сохранить видеофайл с помощью инструмента «Сохранить анимацию» (Рисунок 13).

Рисунок 13

Все детали, созданные в данной статье, а также анимация зацепления двух зубчатых колес, можно скачать тут >>>скачать.

Урок 18. Зубчатое колесо в Компасе

Здравствуйте уважаемые читатели! На этом уроке посмотрим, как создать зубчатое колесо в Компасе при помощи библиотеки Валы и механические передачи 2d.

Библиотека эта доступна в полной версии Компаса, скачать бесплатно ознакомительную версию можно на официальном сайте компании Аскон.

Я буду выполнять работу в Компас 3dv14.

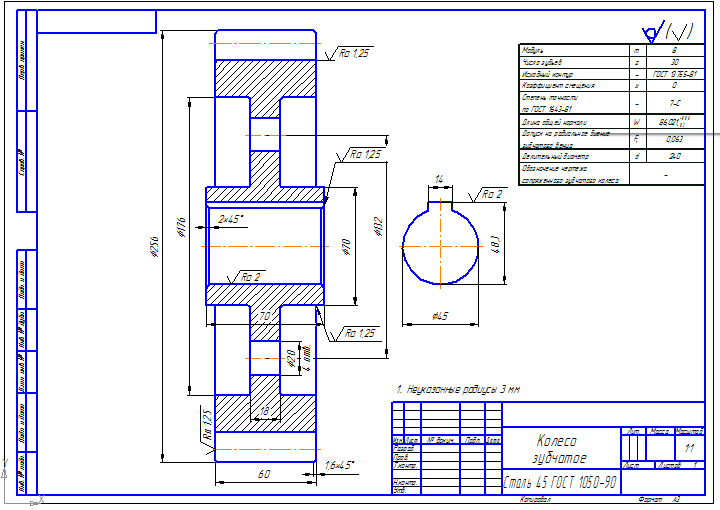
В качестве примера воспользуюсь чертежом колеса, расположенным в учебнике С. К. Боголюбова, 1985 г., стр. 236.

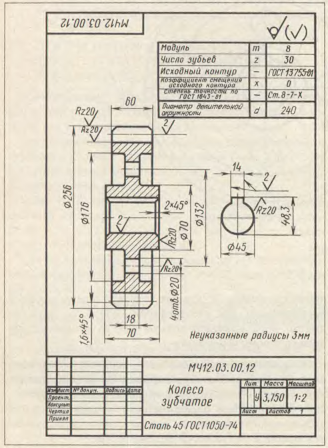
Основные параметры колеса рассчитаны, задан модуль и число зубьев. Можно приступать к выполнению работы.

Зубчатое колесо в Компасе

1 Создаем документ Чертеж, устанавливаем формат А3, ориентация – горизонтальная.

2 Вызываем библиотеку Валы и механические передачи 2d, нажав на кнопку Менеджер библиотек на стандартной панели. Выбираем вкладку Расчет и построение. Дважды щелкаем по нужной библиотеке.

3 Дважды нажимаем на команду Построение модели.

4 В окне нажимаем Создание новой модели, строить будем в разрезе.

5 Фиксируем первую точку изображения и приступаем к построению чертежа зубчатого колеса.

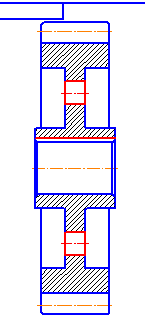
5.1 Для начала построим выступающую часть ступицы. Во внешнем контуре выбираем Цилиндрическую ступень.

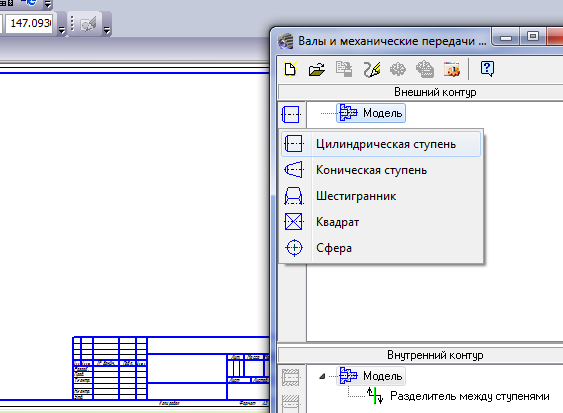
Задаем ее размеры: диаметр 70 мм, длина – 5 мм.

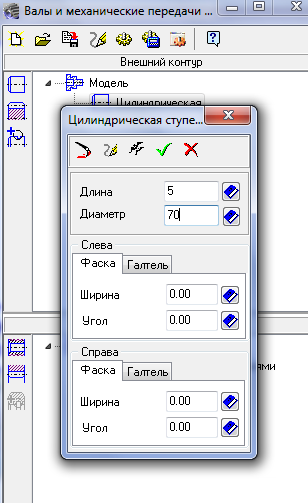
Нажимаем кнопку Ок (зеленая стрелочка).

5.2 Т. К. вычерчивать будем прямозубое зубчатое колесо, то во вкладке Элементы механических передач, выбираем Цилиндрическую шестерню.

5.2 Задаем фаски справа и слева по 1,6 мм и запускаем расчет по межосевому расстоянию.

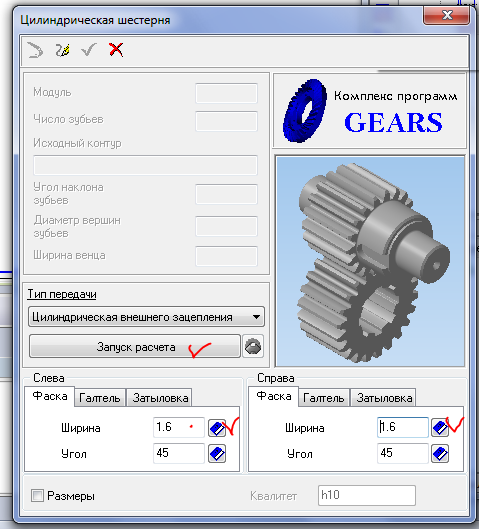
5.3 В окошко вводим значения параметров передачи, рассчитываем межосевое расстояние. Переходим на вторую страницу.

5.4 Нажимаем на кнопку Расчет, дожидаемся появления результатов проверки внесенных данных системой, и, если все в норме, нажимаем кнопку Закончить расчеты.

5.5 Выбираем шестерню или колесо (в данном случае без разницы). Жмем Ок.

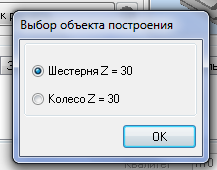
5.6 Дочерчиваем часть ступицы.

5.7 Оформляем внутренний контур колеса. Выбираем внутреннюю цилиндрическую ступень, делаем в ней фаски 2*45º

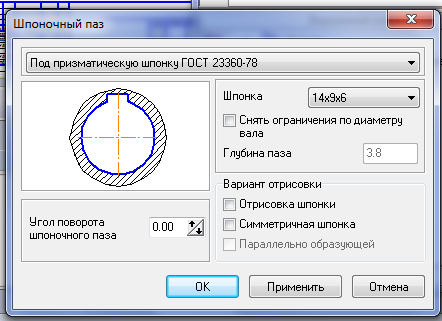
5.8 Выбираем дополнительные построения и строим шпоночный паз, размеры его определяются автоматически.

5.9 Возвращаемся к внешнему контуру и создаем кольцевые пазы и отверстия (дополнительные построения).

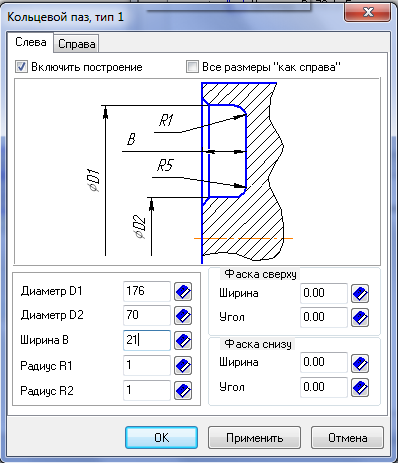
Колесо почти готово.

5.10 Нажимаем на кнопку дополнительных построений во внешнем контуре, выбираем построение таблицы параметров. Создаем упрощенную таблицу.

5.11 Сгенерируем твердотельную модель колеса.

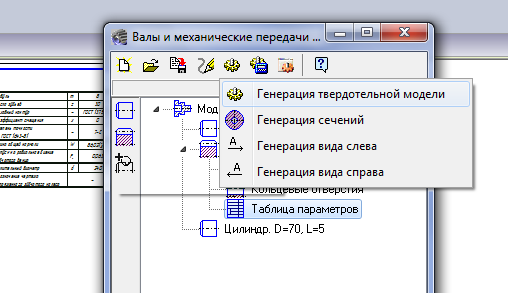
Нажимаем Сохранить модель и выйти.

Чертеж зубчатого колеса в Компасе остается дополнить построенным от руки контуром отверстия для вала со шпоночным пазом, проставленными размерами и нанесенной шероховатостью поверхности.

Технические требования и знак неуказанной шероховатости берем из меню Вставка.

Посмотрите урок, если что-то непонятно.

Зубчатое колесо в Компасе с помощью библиотеки построить достаточно просто и быстро. А это, согласитесь, большой плюс.

Чертежи зубчатого колеса

При создании технологического процесса производства и проведении других проектных работ зачастую создаются чертежи. Они отражают особенности геометрии изделия, а также его размеры и многие другие моменты. Чертежи зубчатого колеса или другого типа выполняются по упрощенной схеме с применением различных условных обозначений. Это связано с тем, что сложная форма изделия создает существенные трудности при ее полной детализации на момент создания чертежей. Оформить рассматриваемый документ с учетом всех требований достаточно сложно, для этого требуются определенные навыки и знания. Сегодня большинство чертежей создается в электронном виде при применении особых программ. Стоит учитывать, что они лишь частично упрощают процесс. Часто проектируется червячная зубчатая передача, чертежи которой можно встретить на самых различных сайтах.

Основные параметры зубчатого колеса

Создавать рассматриваемую конструкцию следует исключительно при заблаговременном создании чертежа, на котором отображаются основные параметры зубчатого колеса. Стоит отметить, что по создаваемой схеме некоторых механизмов также можно определить неправильный выбор основных параметров. В большинстве случае также делается упрощенный чертеж вала, за счет чего можно сразу определить принцип действия механизма.

Основными параметры, которые относятся к зубчатым колесам, являются:

1. Делительная окружность пары зубчатых колес. Данный показатель применяется в случае проектирования зубчатой пары самого различного типа. Она определяется соприкасающимися окружностями, которые катаются одна по другой без скольжения. Применяется для обозначения момента зацепления и сопряжения. Для обозначения на чертеже применяется буква d. Стоит учитывать, что само обозначение зачастую не проставляется, а только указывается соответствующий размер.
2. Окружный шаг зубьев. Этот параметр применяется для определения расстояния между отдельными профильными поверхностями соседних зубьев. Подобный показатель вычисляется путем разделения значения делительной окружности на число зубьев.
3. Число зубьев. Достаточно важным моментом назовем то, что на чертеже не проводится отображение всех зубьев. В некоторых случаях проводится создание эскиза нескольких зубьев. За счет этого существенно упрощается поставленная задача по созданию рассматриваемого документа.
4. В создаваемой таблице в обязательном порядке указывается число зубьев. Подобная информация позволяет проводить расчеты и определение других наиболее важных параметров.
5. Длина делительной окружности.
6. Основные геометрические параметры зуба. Основной частью зубчатых колес является именно зуб. Он применяется

Кроме этого, при создании технической документации уделяется внимание тому, в каких условиях происходит зацепление.

Если не учитывать основные параметры, то есть вероятность быстрого износа поверхности и появления многих других проблем.

Правила оформления чертежей

Довольно большое распространение получил чертеж цилиндрической зубчатой передачи. При его создании учитывается достаточно большое количество различных параметров. Правила выполнения рассматриваемой технической документации характеризуются следующими особенностями:

1. Для начала проводится заполнение таблицы, в которой указываются основные параметры. Примером можно назвать нормальный исходный контур, коэффициент смещения, степень точности проводимой работы и вид сопряжения по нормам бокового зазора. Вторая часть таблицы применяется для указания основных параметров венца для контроля взаимного расположение профилей. Третья часть таблицы требуется для указания менее важных параметров, без которых чертеж конического зубчатого колеса будет неполным.
2. Создавая чертеж цилиндрического зубчатого колеса проводятся расчеты основных параметров, которые зависят от делительного конуса. Для проектирования применяется два дополнительных делительных конуса: внешний и внутренний. Чертежи зубчатых колес шестерен также можно создать при учете внешнего модуля окружности и числа зубьев. Если на документе отображается механизм, то число зубьев обоих колес обозначаются z1 и z Стоит учитывать, что чертеж червячного колеса существенно отличается от цилиндрического.
3. Прежде чем приступать к непосредственному вычерчиванию линий нужно провести расчет все основных параметров, которые также отобразятся в содержимом документа. Оформление чертежа зубчатого колеса начинается с создания фронтального разреза. Он также требуется для определения основных параметров косозубого или прямозубого колеса.
4. Следующий шаг заключается в создании двух делительных конусов с общей образующей. Правила выполнения чертежей предусматривают создание двух линий, которые отходят от делительного конуса колеса. Они должны быть расположены исключительно под прямым углом к образующей. За счет этого образуется внешний дополнительный конус.
5. На месте пересечения образующей откладываются дополнительные точки. За счет этого формируется высота головки и размер ножки. Создавая зубчатые колеса по ГОСТ откладывается размер высоты ножки вдоль образующей дополнительного конуса, за счет чего получается конус впадин.
6. По образующей делительного конуса откладывается размер длины зуба. Типовое изображение на чертеже этого элемента также достаточно просто, основные параметры подсчитываются.

Следующий шаг заключается в создании вида слева. Госстандарт предусматривает наличие подобного вида, при создании самых различных технологических карт. Среди особенностей создания подобного вида отметим нижеприведенные моменты:

1. Для конических колес был создан ГОСТ 2.402-68. Информация, которая содержится в этом документе, определяет необходимость в указании лишь двух окружностей зубчатого венца. Применяется обозначение определяет то, что основная часть указывается сплошной линией, делительная окружность штрихпунктирной. Подобное способ отображения чертежа позволяет указать основные данные. Если создается шевронное соединение, то нужно уделить внимание другим ГОСТам, в которых также отображены определенные стандарты.
2. Согласно установленным норам в ГОСТ 2.405-75 часть размеров проставляется на изображении, другая указывается в таблице параметров. За счет этого можно существенно повысить степень читаемости чертежа. Распространенный пример заключается в указании модуля и другой подобной информации.

Таблица различных данных отображается в большинстве случаев справа в верхнем углу. Чтение подобной информации, как правило, не создает трудностей, так как она отображена числами.

Скачать ГОСТ 2.402-68

Среди других особенностей отображения информации можно отметить следующие моменты:

1. На изображении наносится диаметр большего основания конуса вершин.
2. Также проводится указание размера от базовой поверхности до большего основания конуса вершин.
3. Не стоит забывать о том, что зубья имеют довольно сложную форму. При производстве уделяется внимание показателю градусов. К примеру, угол конуса вершин внешнего дополнительного конуса.
4. При наличии внешнего дополнительного конуса также проводится указание ширины зубчатого венца.
5. Во всех случаях проводится указание размера базового расстояния. Этот показатель в большинстве случаев применяется в случае расчетов второстепенных размеров. Именно поэтому следует уделять больше внимания тому, какие именно базовые показатели следует указывать в конкретном случае.
6. Фаски являются неотъемлемой частью всех зубчатых колес. Как правило, она выполняется под углом 45 градусов и составляет всего пару миллиметров. Радиус скругления на кромках зуба также должен указываться.

В конструкторской документации ЕСКД указывается и некоторая другая информация, которая позволяет получить изделие с требуемыми параметрами. Примером можно назвать нанесение показателя шероховатости. Качественные изделия характеризуются довольно низким значение шероховатости, что достигается путем шлифования и полирования. Подобный показатель наносится на чертеж при помощи специальной полки.

Размер, ширина, габариты проставляются практически во всех случаях. Они позволяют сразу подобрать наиболее подходящую заготовку, в качестве которой часто применяется цилиндр. Не стоит забывать и про внутренний диаметр отверстия, которое предназначено для посадки на вал. Исключить вероятность прокручивания шестерни можно за счет создания шпоночного отверстия.

Чертеж, который применяется для изготовления пластмассового зубчатого колеса, несколько отличается от тех, по которым проводится производство стальных изделий. Это связано с эксплуатационными характеристиками изделия, особенностями применяемого материала при его изготовлении. Эскиз также изготавливается в соответствии со стандартами, в таблице указывается тип применяемого материала при изготовлении.

Довольно много внимания уделяется именно нанесению основных размеров. Часто встречается ситуация, когда из-за небольших размеров изделия или сложности отображаемого механизма нет достаточного количества свободного пространства. Инженер, которые занимается создание чертежа, должен предусмотреть правильное расположение всех размерных линий. Стоит учитывать, что определение размеров путем измерения линий на производстве не проводится, то есть все требуемые показатели для изготовления детали проставляются. В некоторых случаях проводится указание базовых размеров, от которых проводится вычисление других.

Довольно распространенным способом решения проблемы с большим количеством размерных линий можно назвать создание различных выносок.

Они существенно упрощают чтение информации.

При применении специальной программы для создания проектной документации следует учитывать, что в настройках указывается тип стрелок и многие другие моменты. В этом случае программ сама считает основные показатели между двумя указанными точками, за счет чего существенно упрощается поставленная задача.

Скачать ГОСТ 2.405-75

В последнее время для создания чертежей зубчатых колес часто применяется программа автокад. Она встречается не только в бюро разработок, но и сборочном конвейере, так как позволяет открывать ранее созданные чертежи и проводить внесение различных изменений. Среди особенностей применения отметим следующие моменты:

1. Чертеж создается в электронном виде, после чего отправляется на печать. Готовый вариант исполнения практически ничем не будет отличаться от электронного, главное правильно выбрать подходящее оборудование.
2. Не стоит предполагать, что применение рассматриваемого программного обеспечения позволит автоматизировать процесс. При применении Автокада также приходится выбирать подходящие способы простановки основных параметров, строить линии и выполнять другую работу.
3. Сложность в применении подобной программы заключается в том, что она имеет просто огромное количество различных инструментов, которые можно использовать для существенного ускорения работы. Правильно использовать подобные инструменты достаточно сложно, для этого нужно иметь определенные навыки.

На сегодняшний день в большинстве случаев применяются именно электронные чертежи. Это можно связать с простотой их использования, а также снижением вероятности допущения ошибок. Вся проектная документация должна создаваться исключительно с учетом масштаба. При применении рассматриваемой программы можно существенно повысить точность размеров.

В заключение отметим, что при работе в программе не стоит забывать о важности применения линий различной толщины и типа. Кроме этого, для их корректного отображения требуется более подходящее печатное оборудование, которое способно отображать линии различной толщины. В противном случае некоторые конструктивные элементы будет практически невозможно отобразить соответствующим образом.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Шестерёнка — методика построения для любой CAD системы

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых постах.

Отписаться от уведомлений вы всегда сможете в профиле автора.

Про моделирование и печать шестеренок здесь написано достаточно. Однако, большинство статей предполагают использование спец. программ. Но, у каждого пользователя есть своя «любимая» программа для моделирования. Кроме того, не все хотят устанавливать и изучать дополнительный софт. Как же моделировать профиль зуба шестерни в программе, где не предусмотрено вычерчивание эвольвентного профиля? Очень просто! Но муторно… 🙂

Нам понадобится любая программа, которая может работать с 2D графикой. Например, ваша любимая программа! Она работает с 3D? Значит и с 2D сможет! 😉 Строим профиль эвольвентного зуба без коррекции. Если кому-то захочется построить корригированный зуб, он может с этим разобраться самостоятельно. Информации полно — и в интернете, и в литературе. Если в вашей шестеренке зубьев больше 17-ти, то вам коррекция не понадобится. Если же зубьев 17 или меньше, то без коррекции возникает «утоньшение» ножки зуба, а при чрезмерной коррекции возникает заострение вершины зуба. Что выбрать? Решать вам.

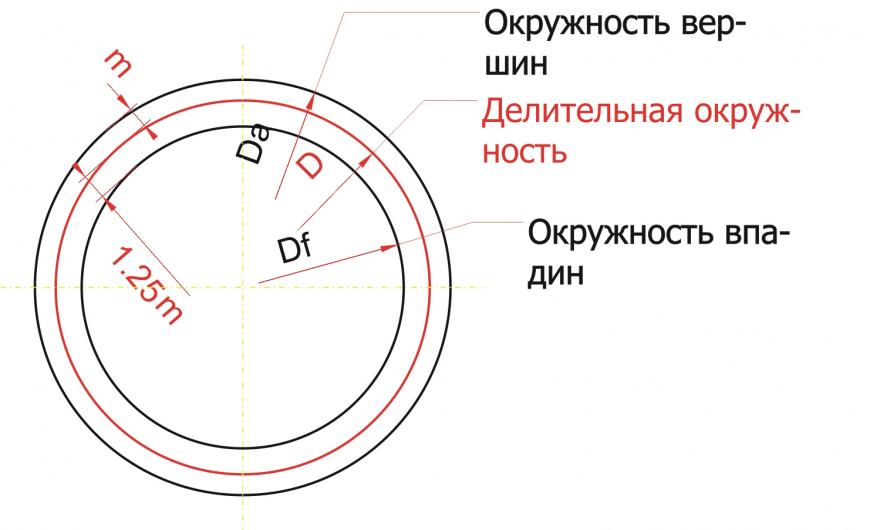
Определяем делительную окружность шестерни. Зачем это нужно? Чтобы определить межосевое расстояние. Т.е. где у вас будет располагаться одна шестерня, а где другая. Сложив диаметры делительных окружностей шестеренок и разделив сумму пополам, вы определите межосевое расстояние.

Чтобы определить диаметр делительной окружности нужно знать два параметра: модуль зуба и количество зубьев. Ну, с количеством зубьев – тут всем все понятно. Количеством зубьев на одной и другой шестерне определяется нужное нам передаточное отношение. Что такое модуль? Чтобы не связываться с числом «пи», инженеры придумали модуль. 🙂 Как вы знаете из курса школьной математики: D= 2 «Пи» R. Так вот, что касается шестеренок, там D = m* z, где D – это диаметр делительной окружности, m – модуль, z – количество зубьев. Модуль – величина, характеризующая размер зуба. Высота зуба равна 2,25 m. Модуль принято выбирать из стандартного ряда величин: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32 (ГОСТ-9563). Можно ли придумать «свой» модуль? Конечно! Но ваша шестеренка будет нестандартная! 😉

Чертим делительную окружность. У кого нет подходящей «проги», чертит на бумаге, фанере или металле! 🙂 От делительной окружности «откладываем» наружу на величину модуля (m) окружность вершин зубьев. Внутрь откладываем модуль и еще четверть модуля (1,25 m) — получаем окружность впадин зубьев. Четверть модуля дается на зазор между зубом другой шестерни и впадиной этой шестерни.

Строим основную окружность. Основная окружность – это окружность, по которой «перекатывается» прямая линия, своим концом вычерчивая эвольвенту. Формула для расчета диаметра основной окружности очень простая: Db = D * cos a, где а – угол рейки 20 градусов. Эта формула нам не нужна! Все гораздо проще. Строим прямую линию через любую точку делительной окружности. Удобнее взять самую высокую точку, на «12 часов». Тогда линия будет горизонтальная. Повернем эту линию на угол в 20 градусов против часовой стрелки. Можно ли повернуть на другой угол? Думаю, можно, но не нужно. 🙂 Кому интересно, ищем в литературе или интернете ответ на вопрос.

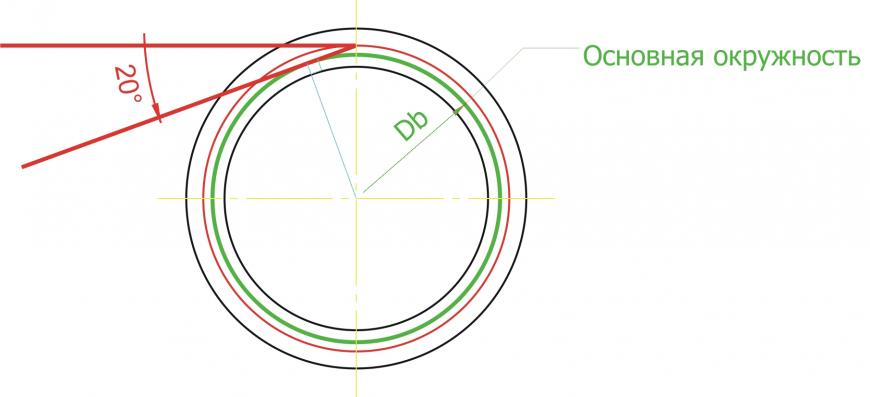
Прямую линию, которую мы получили, будем поворачивать вокруг центра шестерни маленькими угловыми шагами. Но, самое главное, при каждом повороте против часовой стрелки будем удлинять нашу линию на длину той дуги основной окружности, которую она прошла. А при повороте по часовой стрелки наша линия будет укорачиваться на ту же величину. Длину дуги или мерим в программе, или считаем по формуле: Длина дуги = (Пи * Db * угол поворота (в градусах)) / 360

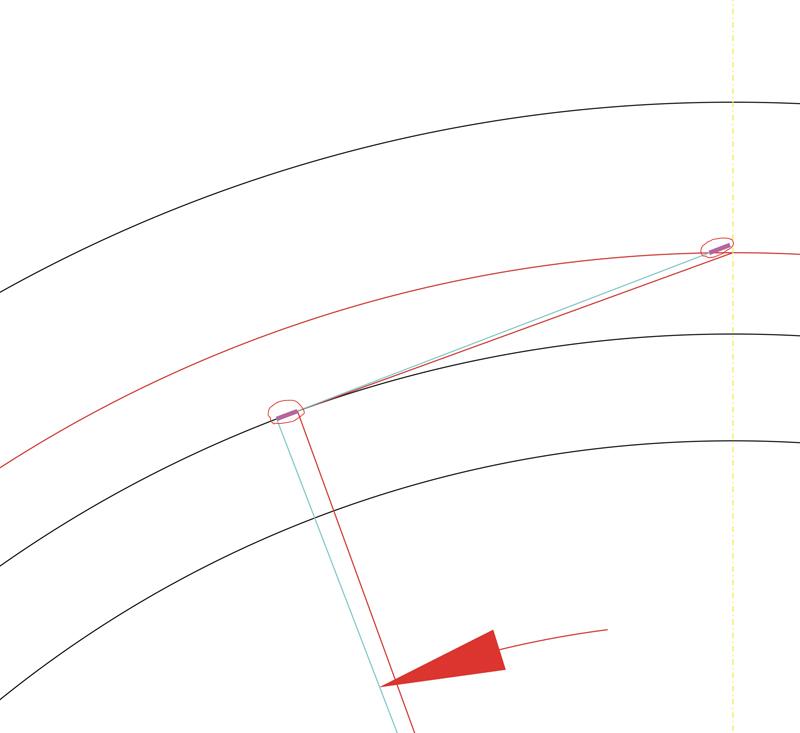
«Прокатываем» прямую линию по основной окружности с нужным угловым шагом. Получаем точки эвольвентного профиля. Чем точнее хотим строить эвольвенту, тем меньший угловой шаг выбираем.

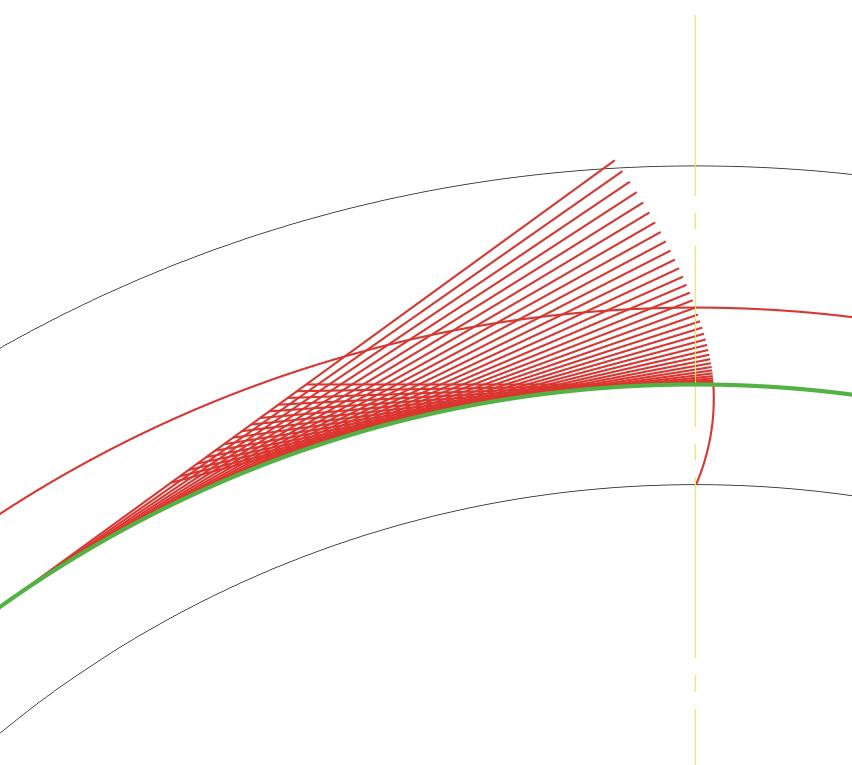
К сожалению, в большинстве программ автоматического проектирования (CAD) не предусмотрено построение эвольвенты. Поэтому эвольвенту строим по точкам либо прямыми, либо дугами, либо сплайнами. При построении эвольвента заканчивается на основной окружности. Оставшуюся часть зуба до впадины можно построить дугой того же радиуса, который получается на трех последних точках. Для 3D печати я рисовал эвольвенту сплайнами. Для лазерной резки металла мне пришлось рисовать эвольвенту дугами. Для лазера нужно создать файл в формате dwg или dxf (для некоторых, почему-то, только dxf). «Понимает» лазер только прямые, дуги и окружности, сплайны не понимает. На лазере можно сделать только прямозубые шестерни.

Делим окружность на такое количество частей, которое в 4 раза больше количества зубьев шестерни. Эвольвенту отзеркаливаем относительно оси зуба и копируем с поворотом нужное количество раз.

Чтобы получить шестерню в объеме, то задаем толщину и получаем прямозубую цилиндрическую шестерню:

Если нужна косозубая шестерня, то вводим наклон зубьев и получаем:

Для получения шевронной шестерни, нужно отзеркалить косозубую шестерню относительно нужной торцевой поверхности:

Как смоделировать коническую шестерню, придумайте сами. 🙂

К вопросу о точности шестеренок. Те шестеренки, которые я распечатал на 3D принтере, сначала вращались, издавая легкое поскрипывание. Прошло некоторое время, и звук прекратился. Шестеренки «притерлись». 🙂

После модернизации принтера, шестеренки не печатал. Возможно, сейчас они напечатаются более точно, и не будут скрипеть.

Для вакуумной машины смоделировал пару – «шестерня-рейка». Их вырезали на лазере:

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых постах.

Отписаться от уведомлений вы всегда сможете в профиле автора.