Формула для расчета периода колебаний пружинного маятника

Все формулы

Все формулы по физике и математике

Темы по физике

• Механика (56)
  • Кинематика (19)
  • Динамика и статика (32)
  • Гидростатика (5)
• Молекулярная физика (25)
  • Уравнение состояния (3)
  • Термодинамика (15)
  • Броуновское движение (6)
  • Прочие формулы по молекулярной физике (1)
• Колебания и волны (22)
• Оптика (9)
  • Геометрическая оптика (3)
  • Физическая оптика (5)
  • Волновая оптика (1)
• Электричество (39)
• Атомная физика (15)
• Ядерная физика (3)

Темы по математике

• Квадратный корень, рациональные переходы (1)
• Квадратный трехчлен (1)
• Координатный метод в стереометрии (1)
• Логарифмы (1)
• Логарифмы, рациональные переходы (1)
• Модуль (1)
• Модуль, рациональные переходы (1)
• Планиметрия (1)
• Прогрессии (1)
• Производная функции (1)
• Степени и корни (1)
• Стереометрия (1)
• Тригонометрия (1)
• Формулы сокращенного умножения (1)

Период пружинного маятника

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Период пружинного маятника — зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается

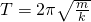
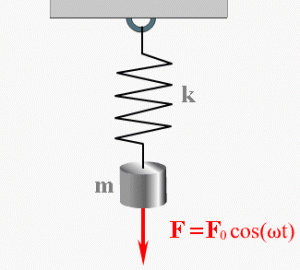
Пружинный маятник — это груз, колеблющийся на пружине. Он совершает возвратно-поступательное движение. Пружинный маятник подчиняется законам движения, по которым можно определить период его колебаний, зная массу груза и жесткость пружины. Период колебаний пружинного маятника не зависит от места его расположения и амплитуды колебаний.

Давайте выведем формулу периода пружинного маятника.

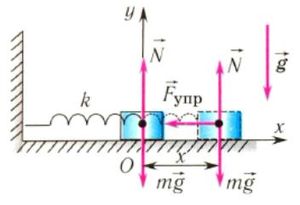
На груз m горизонтального пружинного маятника действуют сила тяжести (mg), сила реакции опоры (N) и сила упругости пружины (Fynp). Запишем второй закон Ньютона для данного случая :

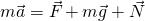
Все проецируем на ось ОХ:

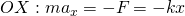
Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора:

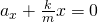
Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:

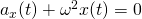
Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:

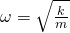
Тогда период колебаний пружинного маятника будет равен:

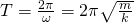
Период математического маятника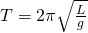

Период физического маятника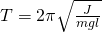

Период крутильного маятника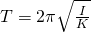

В Формуле мы использовали :

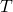— Период пружинного маятника маятника

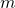— Масса груза

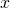— Изменение длины пружины

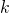— Коэффициент упругости пружины

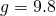— Ускорение свободного падения

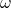— Циклическая частота пружинного маятника

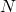— Сила реакции опоры

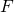— Сила упругости

Формула периода колебаний пружинного маятника

Период — это минимальное время, за которое совершается одно полное колебательное движение.

Обозначают период буквой $T$.

где $Delta t$ — время колебаний; $N$ — число полных колебаний.

Уравнение колебаний пружинного маятника

Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе.

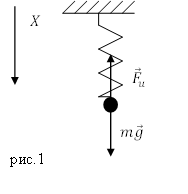
Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:

Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:

Ускорение груза запишем, помня, что движение происходит по оси X, как:

Второй закон Ньютона для груза принимает вид:

Учтем равенство (2), формулу (5) преобразуем к виду:

Если ввести обозначение: $^2_0=frac$, то уравнение колебаний запишем как:

где $^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:

где $_0=sqrt>>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $<(omega >_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

Формулы периода колебаний пружинного маятника

Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые промежутки времени, которые называют периодом колебаний. Обозначают период буквой T.

Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($nu $):

Период связан с циклической частотой колебаний как:

Выше мы получали для пружинного маятника $_0=sqrt>$, следовательно, период колебаний пружинного маятника равен:

Формула периода колебаний пружинного маятника (11) показывает, что $T$ зависит от массы груза, прикрепленного к пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Данное свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, появляется зависимость колебаний от амплитуды. Подчеркнем, что формула (11) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.

Примеры задач на период колебаний

Задание. Пружинный маятник совершил 50 полных колебаний за время равное 10 с . Каков период колебаний маятника? Чему равна частота этих колебаний?

Решение. Так как период — это минимальное время необходимое маятнику для совершения одного полного колебания, то найдем его как:

Частота — величина обратная периоду, следовательно:

Вычислим частоту колебаний:

Ответ. $1) T=0,2$ с; 2) 5Гц

Задание.Две пружины, имеющие коэффициенты упругости $k_1$ и $k_2$ соединены параллельно (рис.2), к системе присоединен груз массы $M$. Каков период колебаний полученного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука?

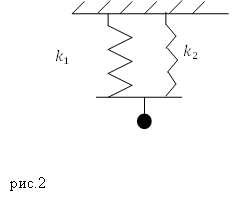
Решение. Воспользуемся формулой для вычисления периода колебаний пружинного маятника:

При параллельном соединении пружин результирующая жесткость системы находится как:

Это означают, что вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:

Ответ. $T=2pi sqrt_2>>$

Механические колебания. Пружинный маятник

Механическими колебаниями называются движения, характеризующиеся определенной повторяемостью во времени.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Гармоническими называются колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (или косинуса).

Пружинный маятник – это колебательная система, состоящая из груза массой т, закрепленного на пружине, совершающая гармонические колебания под действием упругой силы 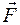, зависящей от величины линейной деформации x по закону Гука (F_x = – kx, где k – жесткость пружины.

Согласно второму закону Ньютона уравнение движения маятника:

.

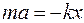Так как ускорение a является второй производной от смещения x (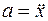), то

или .

Если обозначить 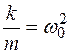, то получим дифференциальное уравнение свободных незатухающих гармонических колебаний пружинного маятника:

.

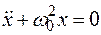Решением этого дифференциального уравнения является функция x(t):

,

где – отклонение тела от положения равновесия в момент времени t;

А – амплитуда колебания, то есть максимальное отклонение колеблющегося тела от положения равновесия;

w – круговая (циклическая) частота;

j – начальная фаза колебания.

Круговая частота , где Т – период колебаний: .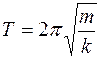

Кинетическая энергия колебаний пружинного маятника:

.

Потенциальная энергия колебаний пружинного маятника:

.

Полная энергия колебаний пружинного маятника:

,

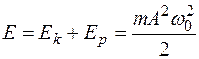откуда видно, что полная энергия свободных незатухающих гармонических колебаний пружинного маятника остается со временем постоянной.

Свободные затухающие гармонические колебания пружинного маятника (рис. 6). Для пружинного маятника массой т, совершающего колебания под действием упругой силы 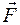(F_x = – kx)с учетомсилы сопротивления 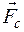, пропорциональной скорости 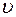движения груза (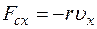), второй закон Ньютона имеет вид:

,

где r – коэффициент сопротивления.

Обозначив и 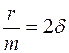( – коэффициент затухания), получим дифференциальное уравнение свободных затухающих гармонических колебаний пружинного маятника:

.

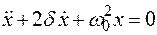Решением этого дифференциального уравнения в случае малых затуханий

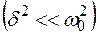является функция x(t):

,

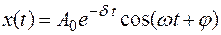где – амплитуда затухающих колебаний в момент времени t;

– начальная амплитуда, т.е. амплитуда в момент времени t = 0,

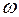– круговая (циклическая) частота: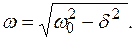

Период затухающих гармонических колебаний пружинного маятника:

.

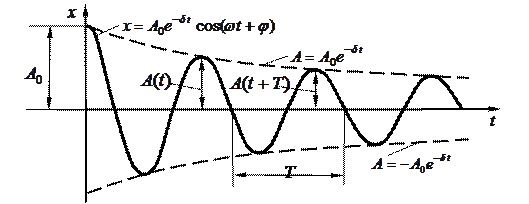
Декремент затухания. Если A(t)и А(t+Т) – амплитуды двух последовательных колебаний (рис. 6), то отношение этих величин называется декрементом затухания .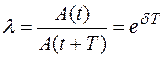

Логарифм называется логарифмическим декрементом затухания :

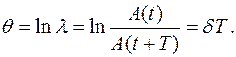
188.64.169.166 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Формула для расчета периода колебаний пружинного маятника

Задача № 1. Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2. На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3. Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4. Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

Задача № 5. Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с 2 .

Задача № 6. Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7. Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

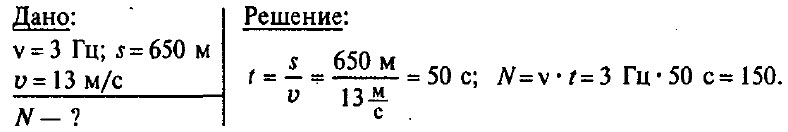
Задача № 8. Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9. Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π 2 = 9,87.)

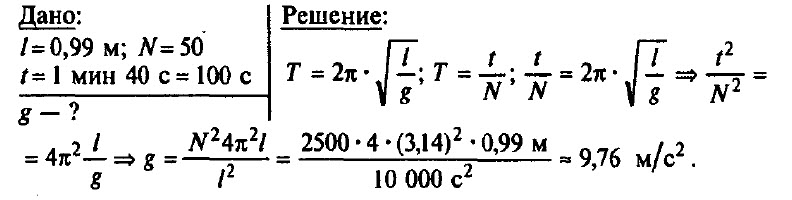
Задача № 10. ОГЭ Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11. ЕГЭ Два математических маятника за одно и то же время совершают — первый N₁ = 30, а второй — N₂ = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:

Период колебаний нитяного и пружинного маятников

Презентация к уроку

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока: рассмотреть процесс колебаний на примере нитяного и пружинного маятников, выяснить зависимость периода колебаний от различных физический величин: длины нити, ускорения свободного падения, коэффициента жесткости и массы.

1. Проверка домашнего задания. (работа по формуле “Скажи ты. )

— Что называется амплитудой колебания; периодом колебания; частотой колебания; циклической частотой?

— Какой буквой обозначается циклическая частота?

— Какая математическая зависимость существует между периодом и частотой колебания?

Учащиеся в парах проверяют домашнюю работу: упражнение №24.

2. Объяснение нового материала. Работа по теме урока.

Учитель. Как вы думаете, от каких величин может завесить период колебаний нитяного маятника?

Ученики. От длины нити и массы груза.

Учитель. Начнем с длины нити. Поставим опыт с двумя маятниками, имеющими разную длину нити, но одинаковую массу (эксперимент).

Ученики. С увеличением длины нити период колебаний увеличивается.

Учитель. А теперь посмотрим как зависит период колебаний от массы груза (эксперимент: маятники имеют одинаковую длину нити и разный вес грузов).

Учащиеся. Период не зависит от массы груза.

Учитель. Но период колебания нитяного маятника зависит еще от одной физической величины. Это ускорение свободного падения. Проведем эксперимент и “поможем “ силе тяжести положив магнит. Теперь при той же массе груза возвращающая сила будет больше.

Ученики. Период уменьшился, а частота увеличилась.

Учитель. А теперь выведем формулу для расчета периода колебания нитяного маятника.

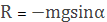
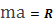
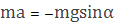
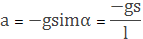
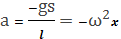
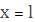
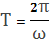
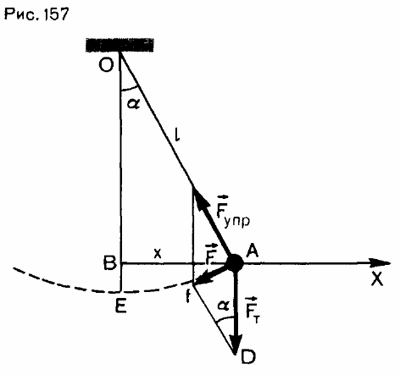
формула Гюйгенса: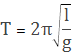

g – ускорение свободного падения.

Это очень важная формула и ее надо запомнить.

Учитель. От чего может зависеть период пружинного маятника?

Ученики. От жесткости пружины, массы груза.

Учитель. Сначала на опыте посмотрим зависимость периода колебаний и жесткости пружины.(эксперимент : две пружины разной жесткости, но одинаковой длины и одинаковой массой груза)

Ученики. Период меньше там, где жесткость больше.

Учитель. А как вы думаете как зависит период от массы груза(эксперимент).

Ученики. Чем больше масса , тем больше и период.

Учитель. А теперь выведем формулу для расчета периода колебания пружинного маятника.

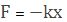— возвращающая сила системы

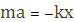
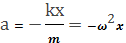
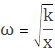— собственная частота системы.

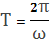
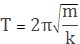
Эту формулу так же запишите на обложку тетради и постарайтесь ее запомнить.

3. Закрепление материала

Решение задач Лукашик В.И.№ 873, 876.879

4.Домашнее задание. Лукашик В.И.№ 875, 877.880.

Список литературы:

1.Л.Э.Генденштейн,В.А.Орлов,Г.Г.Никифоров “Как научить решать задачи по физике (основная школа ). Подготовка к ГИА.

2. С.Е.Полянский “Поурочные разработки по физике”.

Свободные колебания. Пружинный маятник

Свободные колебания могут совершаться под действием внутренних сил только после выведения из положения равновесия всей системы.

Чтобы колебания совершались согласно гармоническому закону, нужно, чтобы сила, возвращающая тело в положение равновесия, была пропорциональна смещению тела из равновесного положения и направлена в сторону, противоположную смещению.

F ( t ) = m a ( t ) = — m ω 2 x ( t ) .

Соотношение говорит о том, что ω является частотой гармонического колебания. Данное свойство характерно для упругой силы в пределах применимости закона Гука:

Силы любой природы, которые удовлетворяют условию, называют квазиупругими.

То есть груз с массой m , прикрепляющийся к пружине жесткости k с неподвижным концом, изображенным на рисунке 2 . 2 . 1 , составляют систему, способную совершать гармонические свободные колебания при отсутствии силы трения.

Груз, располагаемый на пружине, называют линейным гармоническим осциллятором.

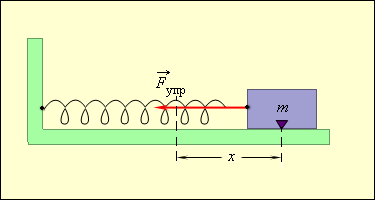
Рисунок 2 . 2 . 1 . Колебания груза на пружине. Трения нет.

Круговая частота

Нахождение круговой частоты ω 0 производится с помощью применения формулы второго закона Ньютона:

m a = — k x = m ω 0 2 x .

Частоту ω 0 называют собственной частотой колебательной системы.

Определение периода гармонических колебаний груза на пружине Т находится из формулы:

T = 2 π ω 0 = 2 π m k .

Горизонтальное расположение системы пружина-груз, сила тяжести компенсируется силой реакции опоры. При подвешивании груза на пружину направление силы тяжести идет по линии движения груза. Положение равновесия растянутой пружины равняется:

x 0 = m g k , тогда как колебания выполняются около нового равновесного состояния. Формулы собственной частоты ω 0 и периода колебаний Т в вышеуказанных выражениях являются справедливыми.

При имеющейся математической связи между ускорением тела а и координатой х поведение колебательной системы характеризуется строгим описанием: ускорение является второй производной координаты тела х по времени t :

Описание второго закона Ньютона с грузом на пружине запишется как:

m a — m x = — k x , или x ¨ + ω 0 2 x = 0 , где свободная частота ω 0 2 = k m .

Если физические системы зависят от формулы x ¨ + ω 0 2 x = 0 , тогда они в состоянии совершать свободные колебательные гармонические движения с различной амплитудой. Это возможно, так как применяется x = x m cos ( ω t + φ 0 ) .

Свободные колебания

Уравнение вида x ¨ + ω 0 2 x = 0 получило название уравнения свободных колебаний. Их физические свойства могут определять только собственную частоту колебаний ω 0 или период Т .

Амплитуда x m и начальная фаза φ 0 находят при помощи способа, который вывел их из состояния равновесия начального момента времени.

При наличии смещенного груза из положения равновесия на расстояние ∆ l и моменте времени, равном t = 0 , производится его опускание без начальной скорости. Тогда x m = ∆ l , φ 0 = 0 . Если груз находился в положении равновесия, то при толчке передается начальная скорость ± υ 0 , отсюда x m = m k υ 0 , φ 0 = ± π 2 .

Амплитуда x m с начальной фазой φ 0 определяются наличием начальных условий.

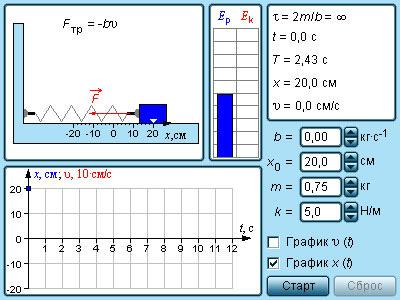
Рисунок 2 . 2 . 2 . Модель свободных колебаний груза на пружине.

Механические колебательные системы отличаются наличием сил упругих деформаций в каждой из них. Рисунок 2 . 2 . 2 показывает угловой аналог гармонического осциллятора, совершающий крутильные колебания. Диск располагается горизонтально и висит на упругой нити, закрепленной в его центре масс. Если его повернуть на угол θ , тогда возникает момент силы упругой деформации кручения M у п р :

Данное выражение не соответствует закону Гука для деформации кручения. Величина x аналогична k жесткости пружины. Запись второго закона Ньютона для вращательного движения диска принимает вид

I ε = M у п р = — x θ или I θ ¨ = — x θ , где моментом инерции обозначается I = I C , а ε – угловое ускорение.

Аналогично с формулой пружинного маятника:

ω 0 = x I , T = 2 π I x .

Применение крутильного маятника замечено в механических часах. Он получил название балансира, в котором создание момента упругих сил производится при помощи спиралевидной пружины.

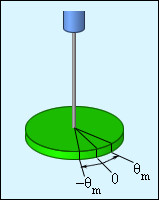
Рисунок 2 . 2 . 3 . Крутильный маятник.