Чему равна потенциальная энергия упруго деформированной пружины
Какие величины определяют потенциальную энергию растянутой пружины
Все формулы по физике и математике
Темы по физике
- Механика (56)
- Кинематика (19)
- Динамика и статика (32)
- Гидростатика (5)
- Молекулярная физика (25)
- Уравнение состояния (3)
- Термодинамика (15)
- Броуновское движение (6)
- Прочие формулы по молекулярной физике (1)
- Колебания и волны (22)
- Оптика (9)
- Геометрическая оптика (3)
- Физическая оптика (5)
- Волновая оптика (1)
- Электричество (39)
- Атомная физика (15)
- Ядерная физика (3)
Темы по математике
- Квадратный корень, рациональные переходы (1)
- Квадратный трехчлен (1)
- Координатный метод в стереометрии (1)
- Логарифмы (1)
- Логарифмы, рациональные переходы (1)
- Модуль (1)
- Модуль, рациональные переходы (1)
- Планиметрия (1)
- Прогрессии (1)
- Производная функции (1)
- Степени и корни (1)
- Стереометрия (1)
- Тригонометрия (1)
- Формулы сокращенного умножения (1)
Потенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.
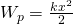
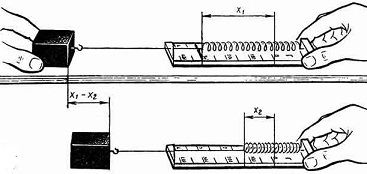
Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем упругую энергию растянутой пружины.
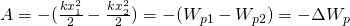
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.
Потенциальная энергия :
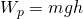
Кинетическая энергия
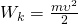
Тут мы использовали :
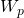 — Потенциальная энергия упруго деформированного тела
— Потенциальная энергия упруго деформированного тела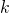 — Коэффициент упругости пружины
— Коэффициент упругости пружины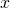 — Деформация пружины
— Деформация пружиныГруз массой m, подвешенный к пружине, совершает колебания с периодом T и амплитудой
Что произойдет с периодом колебаний, максимальной потенциальной энергией пружины и частотой колебаний, если при неизменной амплитуде уменьшить массу груза?
Для каждой величины определите соответствующий характер изменения:
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Период колебаний связан с массой груза и жесткостью пружины k соотношением
При уменьшении массы период колебаний уменьшится. Частота обратно пропорциональна периоду, значит, частота увеличится.
С максимальной потенциальной энергией пружины все немного сложнее. Для ответа на вопрос, что с ней произойдет существенно, что пружина ориентирована вертикально (для горизонтального пружинного маятника при неизменной амплитуде данная величина, естественно, останется неизменной). Действительно, когда к вертикальной пружине подвешивают груз, она сразу немного растягивается, чтобы уравновесить силу тяжести, действующую на груз. Определим это начальное растяжение:
Именно это состояние является положением равновесия для вертикального пружинного маятника, колебания происходят вокруг него, груз поднимается и опускается из этого положения на величину амплитуды. При движении вниз из положения равновесия пружина продолжает растягиваться, а значит, потенциальная энергия пружины продолжает увеличиваться. При движении вверх из положения равновесия, сперва деформация пружины уменьшается, а если
то пружины начнет сжиматься. Максимальной потенциальной энергии пружины соответствует состояние, когда она максимально растянута, а значит, в нашем случае, это положение, когда груз опустился максимально вниз. Таким образом, максимальная потенциальная энергия пружины равна
Из этой формулы видно, что для вертикального пружинного маятника при неизменной амплитуде и уменьшении массы груза максимальная потенциальная энергия пружины уменьшится.
Встречается довольно большое количество различных механизмов, частью которых является пружина. Этот конструктивный элемент характеризуется довольно большим количество различных особенностей, которые должны учитываться. Примером можно назвать понятие потенциальной энергии пружины. Рассмотрим все особенности данного вопроса подробнее.

Понятие потенциальной энергии пружины
При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:
- Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
- Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
- После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах. Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.

Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.
Закон сохранения механической энергии
Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.
Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.
Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.

Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.
Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.
Динамика твердого тела
Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела
Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.
Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.

Момент силы и момент импульса относительно оси
Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.
Момент импульса – величина, которая применяется для определения количества вращательного движения.
Среди особенностей подобного показателя можно отметить следующее:
- Масса вращения. Объект может характеризоваться различной массой.
- Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
- Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.


Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.
Уравнение движения вращающегося тела
Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:
- Прямая, которая соединяет две точки, выступает в качестве оси вращения.
- Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
- Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.
Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Потенциальная энергия пружины
Встречается довольно большое количество различных механизмов, частью которых является пружина. Этот конструктивный элемент характеризуется довольно большим количество различных особенностей, которые должны учитываться. Примером можно назвать понятие потенциальной энергии пружины. Рассмотрим все особенности данного вопроса подробнее.

Понятие потенциальной энергии пружины
При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:
- Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
- Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
- После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах. Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.

Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.
Закон сохранения механической энергии
Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.
Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.
Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.

Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.
Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.
Динамика твердого тела
Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела
Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.
Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.

Момент силы и момент импульса относительно оси
Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.
Момент импульса – величина, которая применяется для определения количества вращательного движения.
Среди особенностей подобного показателя можно отметить следующее:
- Масса вращения. Объект может характеризоваться различной массой.
- Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
- Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.


Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.
Уравнение движения вращающегося тела
Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:
- Прямая, которая соединяет две точки, выступает в качестве оси вращения.
- Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
- Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.
Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Работа силы упругости. Потенциальная энергия упруго деформированного тела
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На данном уроке мы поговорим о том, что такое сила упругости, научимся вычислять ее работу, введя в рассмотрение новую разновидность потенциальной энергии, а также поговорим о потенциальной энергии и об упругом столкновении тел.
Введение
На прошлом уроке мы с вами показали, что для применения теоремы об изменении кинетической энергии мы должны уметь вычислять работу основных сил в природе. И мы уже научились это делать на примере работы силы тяжести. Было показано, что эту величину очень просто рассчитать, если ввести в рассмотрение новый вид энергии – потенциальную энергию тела, притягивающуюся к земле. Сегодня сделаем то же самое для силы упругости.
Рассмотрим простую систему: массивный груз, прикрепленный к пружине (см. рис. 1).

Рис. 1. Груз, прикрепленный к пружине
Пусть изначально система находится в состоянии равновесия, то есть пружина не деформированная, и груз покоится. Выведем эту систему из равновесия и сделаем так, чтобы пружина стала в сжатом состоянии (см. рис. 2).

Рис. 2. Система выведена из равновесия
Если направить ось ОХ так, как показано на рис. 2, и расположить начало координат там, где до начала сжатия был расположен центр груза, то проекцию возникающей силы упругости на нашу ось ОХ можно записать в виде:
 ,
,где k – жесткость пружины,
 величина деформации пружины. Если предоставить пружину самой себе, то груз будет смещаться влево, при этом сила упругости будет совершать работу. Предположим, что левый конец пружины вместе с грузом переместился из положения А в положение В (см. рис. 3).
величина деформации пружины. Если предоставить пружину самой себе, то груз будет смещаться влево, при этом сила упругости будет совершать работу. Предположим, что левый конец пружины вместе с грузом переместился из положения А в положение В (см. рис. 3).
Рис. 3. Перемещение груза
В этом положении деформация пружины равна уже не
 , а
, а  . А перемещение конца пружины и одновременно перемещение центра груза равно разности координат
. А перемещение конца пружины и одновременно перемещение центра груза равно разности координат  . Попытаемся вычислить работу силы упругости, совершенную при таком движении груза.
. Попытаемся вычислить работу силы упругости, совершенную при таком движении груза.Вычисление работы силы упругости
Груз совершил известное перемещение, величину силы упругости мы также знаем, векторы перемещения и силы упругости параллельны. Казалось бы, все ясно – нужно умножить величину силы на величину перемещения и получить значение работы. Однако здесь не все так просто – разберемся почему.
О чем нам говорит формула, которая выражает величину силы упругости? О том, что сила упругости – величина не постоянная, она меняется по мере перемещения груза. И действительно, величина этой силы, как мы видим из формулы, зависит от координаты центра груза. Формула же для работы силы, которую мы применяли раньше, справедлива лишь в том случае, если сила не меняет свою величину по мере движения. Как же тогда быть? Один из вариантов выхода из данной ситуации мог бы состоять в том, что мы применим такой же метод, который применялся нами ранее в разделе кинематика при расчете перемещения тела, движущегося равноускоренно.
Можно всю траекторию движения груза разбить на очень маленькие участки (участки, в пределах которых силу упругости можно считать практически постоянной). Далее в пределах каждого такого участка мы можем рассчитать работу силы упругости ввиду ее практического постоянства. Затем работа на всей области движения груза будет складываться из всех этих маленьких работ на этих участках. Таким образом, мы сможем посчитать работу силы упругости на всей траектории движения груза. На рис. 4 приведены детали такого расчета.

Рис. 4. Зависимость силы упругости от координаты движения
Видно, что если отложить на графике зависимость модуля силы упругости от модуля координаты груза, затем проделать описанное выше разбиение на маленькие участки, то величина работы на каждом маленьком участке численно равна площади фигуры, ограниченной графиком: осью абсцисс и двумя перпендикулярами к этой оси (см. рис. 5).

Рис. 5. Площадь фигуры
Если просуммировать значение работы на каждом участке (площадь маленьких фигур), то получим площадь большой фигуры, показанной на рис. 6.

Рис. 6. Площадь большой фигуры
Поскольку данная фигура является прямоугольной трапецией, то мы можем воспользоваться формулой для расчета площади такой фигуры – это полусумма оснований, умноженная на высоту. В результате преобразований получим такую формулу – работа равна разности между величиной:

К этому результату можно прийти и несколько иным способом. Для вычисления работы силы упругости в этом способе необходимо просто взять среднее значение силы упругости и умножить его на перемещение тела. Это утверждение можно записать как:
 ,
,где
 среднее значение силы упругости, которое равно полусумме начального и конечного ее значений. Если данное выражение
среднее значение силы упругости, которое равно полусумме начального и конечного ее значений. Если данное выражение  подставить в формулу для работы, то при помощи простых алгебраических преобразований мы получим то же самое выражение, что получали ранее:
подставить в формулу для работы, то при помощи простых алгебраических преобразований мы получим то же самое выражение, что получали ранее:
Как видно из этой формулы, работа зависит лишь от начальной и конечной координаты центра груза, и еще одно замечание: как видно из последней формулы, работа силы упругости никоим образом не зависит от массы груза. Это обусловлено тем, что и сама сила упругости не зависит от этой массы.
Теперь внимательнее посмотрим на последнюю формулу – если вынести -1 за скобки, то получим, что работа есть взятая со знаком минус разность между значениями некоторой величины, равной половине произведения жесткости пружины на квадрат ее удлинения в конечный и начальный моменты времени.

Вспомним, как мы поступили при расчете работы силы тяжести на прошлом уроке. В тот раз мы столкнулись с новой для нас физической величиной, разность между значениями которой в конечной и начальной моменты времени равнялась взятой со знаком « — » работе силы тяжести. Это величина, равная произведению массы тела на ускорение свободного падения и высоту, на которую было поднято тело над некоторым уровнем, мы назвали потенциальной энергией тела, поднятого над землей.
Потенциальная энергия упруго деформированного тела
Здесь поступим аналогичным образом. Величину, равную половине произведения жесткости пружины на квадрат ее удлинения, назовем потенциальной энергией деформированной пружины. Мы имеем право это сделать, поскольку изменение данной величины, взятой с обратным знаком, равно работе силы упругости. Теперь формулу для вычисления работы силы упругости можно озвучить по-другому: работа силы упругости равна изменению потенциальной энергии упруго деформированного тела (пружины), взятому с обратным знаком:

Работа силы упругости, как и работа силы тяжести, зависит только от начального и конечного положения центра груза – это означает, что работа силы упругости не зависит от формы траектории груза, а в том случае, когда траектория является замкнутой, работа силы упругости равна 0.
Если за начало отсчета принять положение груза при недеформированной пружине, а после принять, что удлинение пружины равно
 (см. рис. 7), то формула для работы силы упругости приобретает вид:
(см. рис. 7), то формула для работы силы упругости приобретает вид:

Рис. 7. Вычисление работы силы упругости
Но
 – это потенциальная энергия пружины при ее удлинении на величину
– это потенциальная энергия пружины при ее удлинении на величину  , следовательно, потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе тела (пружины) в состояние, в котором его деформация равна 0.
, следовательно, потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе тела (пружины) в состояние, в котором его деформация равна 0.Когда мы описывали потенциальную энергию тела, поднятого над землей, мы говорили, что потенциальная энергия – это энергия взаимодействия тел и в том случае это была энергия взаимодействия двух тел – груза и земли. Что касается силы упругости, то о ней можно сказать почти то же самое – это тоже энергия взаимодействия, однако теперь это энергия взаимодействия не различных тел, а частей одного и того же тела – в нашем случае это энергия взаимодействия частей пружины.
Теперь рассмотрим задачу.
Задача
Динамометр, рассчитанный на 40 Н, имеет пружину жесткостью 500
 . Какую работу нужно совершить, чтобы растянуть пружину от середины шкалы до последнего деления?
. Какую работу нужно совершить, чтобы растянуть пружину от середины шкалы до последнего деления?В условии нам не дано значений удлинения пружины динамометра, поэтому введем его сами. Пусть удлинение пружины на середине шкалы равно
 (см. рис. 8).
(см. рис. 8).
Рис. 8. Удлинение шкалы
Следовательно, когда пружина растянута с максимальной силой, то удлинение равно
 . Воспользуемся для последнего случая законом Гука, поскольку мы знаем значение максимальной силы и жесткости пружины.
. Воспользуемся для последнего случая законом Гука, поскольку мы знаем значение максимальной силы и жесткости пружины.

Следовательно, нам необходимо рассчитать работу при удлинении от 4 см до 8 см. Воспользуемся формулой, полученной на уроке:

Работа равна разности между значениями потенциальной энергии пружины, растянутой до полного удлинения и до полвины.
Ответ:
 .
.Теперь мы с вами можем рассчитывать потенциальную энергию тела, поднятого над землей, и потенциальную энергию тела, которое испытывает упругую деформацию.
Список литературы
1. Соколович Ю.А., Богданова Г.С Физика: справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
2. Перышкин А.В. Физика: учебник 10 класс. – Издательство: Дрофа.: 2010. – 192 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт fizika.in (Источник)
2. Интернет-сайт Единой коллекции цифровых образовательных ресурсов (Источник)
3. Интернет-сайт объединения учителей физики Санкт-Петербурга (Источник)
Домашнее задание
1. Что такое сила упругости?
2. Напишите формулу, по которой можно найти работу силы упругости.
3. Что такое потенциальная энергия тела?
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.


Все формулы
Все формулы по физике и математике
Темы по физике
- Механика (56)
- Кинематика (19)
- Динамика и статика (32)
- Гидростатика (5)
- Молекулярная физика (25)
- Уравнение состояния (3)
- Термодинамика (15)
- Броуновское движение (6)
- Прочие формулы по молекулярной физике (1)
- Колебания и волны (22)
- Оптика (9)
- Геометрическая оптика (3)
- Физическая оптика (5)
- Волновая оптика (1)
- Электричество (39)
- Атомная физика (15)
- Ядерная физика (3)
Темы по математике
- Квадратный корень, рациональные переходы (1)
- Квадратный трехчлен (1)
- Координатный метод в стереометрии (1)
- Логарифмы (1)
- Логарифмы, рациональные переходы (1)
- Модуль (1)
- Модуль, рациональные переходы (1)
- Планиметрия (1)
- Прогрессии (1)
- Производная функции (1)
- Степени и корни (1)
- Стереометрия (1)
- Тригонометрия (1)
- Формулы сокращенного умножения (1)
Потенциальная энергия упруго деформированного тела
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДАПотенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.
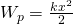
Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем упругую энергию растянутой пружины.

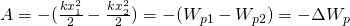
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.
Потенциальная энергия :
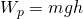
Кинетическая энергия
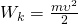
Тут мы использовали :
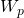 — Потенциальная энергия упруго деформированного тела
— Потенциальная энергия упруго деформированного тела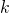 — Коэффициент упругости пружины
— Коэффициент упругости пружины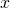 — Деформация пружины
— Деформация пружиныЧему равна потенциальная энергия упруго деформированной пружины
Если к растянутой пружине прикрепить некоторое тело, то пружина будет действовать на него с некоторой силой, под действием которой тело начнет смещаться, то есть будет совершать работу.
Раз пружина способна совершать работу, то она обладает потенциальной энергией.
Формула нахождения потенциальной энергии деформированной пружины:

 — коэффициент жёсткости;
— коэффициент жёсткости;
 — расстояние, на которое растягивают пружину;
— расстояние, на которое растягивают пружину;Таким не хитрым образом мы познакомились с «потенциальная энергия деформированной пружины»!
Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело (например, сжатая пружина, растянутый стержень и т.п.). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (например, от расстояния между соседними витками пружины).
Определим работу, которую необходимо затратить для растяжения (или сжатия) пружины на величину «x» (рис.3.8). Будем считать, что пружина подчиняется закону Гука, т.е. упругая сила пропорциональна деформации. Будем проводить растяжение пружины очень медленно, чтобы силу
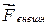 , с которой мы действуем на пружину, можно было все время считать равной по величине упругой силе
, с которой мы действуем на пружину, можно было все время считать равной по величине упругой силе 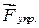 . Далее будем считать, что сила действует в направлении перемещения, т.е.
. Далее будем считать, что сила действует в направлении перемещения, т.е. 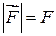 .
.
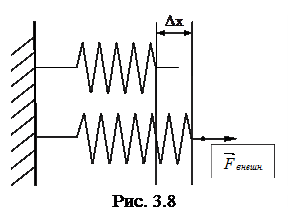 Исходя из предыдущего, можно записать Fвнешн. = -Fупр. = kx, где x – удлинение пружины, k – коэффициент жесткости пружины, а согласно закону Гука направление упругой силы и перемещения противоположны (силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) и имеют, в конечном счете, электрическую природу).
Исходя из предыдущего, можно записать Fвнешн. = -Fупр. = kx, где x – удлинение пружины, k – коэффициент жесткости пружины, а согласно закону Гука направление упругой силы и перемещения противоположны (силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) и имеют, в конечном счете, электрическую природу).Пусть под действием силы
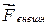 пружина растянулась на dx, тогда dA=F·dx=k·x·dx.
пружина растянулась на dx, тогда dA=F·dx=k·x·dx.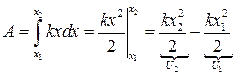 ;
;Эта работа идет на увеличение потенциальной энергии пружины. В предположении, что потенциальная энергия недеформированной пружины равна «0» (U1 = 0) получаем
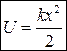 (3.12)
(3.12)– потенциальная энергия упругой деформации пружины.
Закон сохранения энергии.
Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m1 и m2. Пусть частицы взаимодействуют друг с другом с силами
 и
и 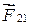 , модули которых зависят от расстояния R12 между частицами. Установлено, что такие силы являются консервативными, т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная сила
, модули которых зависят от расстояния R12 между частицами. Установлено, что такие силы являются консервативными, т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная сила 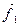 и внешняя неконсервативная сила
и внешняя неконсервативная сила  . Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:
. Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:
Умножим каждое уравнение на
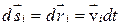 и сложим полученные выражения.
и сложим полученные выражения.
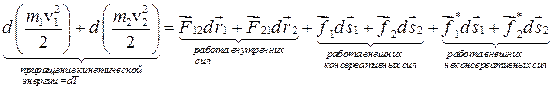
1. Распишем первый член в правой части.
Работа внутренних сил равна
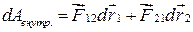 . Для замкнутой системы
. Для замкнутой системы  , а
, а 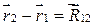 , где
, где  и
и  – радиус-векторы частиц.
– радиус-векторы частиц. .
.Учитывая, что силы
 и
и 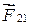 имеют величину, зависящую только от расстояния и направлены вдоль соединяющей их прямой (это справедливо, например, для сил кулоновского или гравитационного взаимодействий), любую из этих сил можно представить в виде, например,
имеют величину, зависящую только от расстояния и направлены вдоль соединяющей их прямой (это справедливо, например, для сил кулоновского или гравитационного взаимодействий), любую из этих сил можно представить в виде, например,  , где f(R12) – некоторая функция R12,
, где f(R12) – некоторая функция R12, 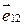 – орт вектора
– орт вектора 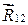 .
.Следовательно,
 .
.Скалярное произведение
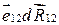 равно приращению dR12 расстояния между частицами, тогда
равно приращению dR12 расстояния между частицами, тогда 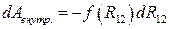 .
.Выражение
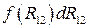 есть приращение некоторой функции
есть приращение некоторой функции 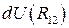 . Следовательно,
. Следовательно,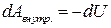 .
.Функция
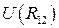 представляет потенциальную энергию взаимодействия.
представляет потенциальную энергию взаимодействия.Работа внутренних сил будет равна
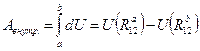 ,
,т.е. не зависит от пути, по которому перемещаются частицы, а определяется начальной и конечной конфигурациями системы. Т.е. силы взаимодействия вида
 являются консервативными.
являются консервативными.Итак, работа внутренних сил равна убыли потенциальной энергии взаимодействия

2. Второй член представляет работу внешних сил и равен убыли потенциальной энергии системы во внешнем поле консервативных сил
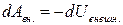
3. Последний член представляет работу неконсервативных внешних сил
 .
.После этих замечаний можно записать
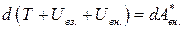
– называется полной механической энергией системы. Если внешние неконсервативные силы отсутствуют, т.е.
 , то
, тоЕ=const – закон сохранения механической энергии.
ОПРЕДЕЛЕНИЕ: полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остается постоянной.
Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, закон сохранения примет вид:
E = T + Uвз. = const
Если в замкнутой системе, кроме консервативных сил действуют неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется. Рассматривая консервативные силы как внешние, получим
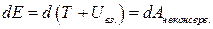
или после интегрирования
 .
.
Анализ закона сохранения показывает, что полная энергия, оставаясь в консервативной системе величиной постоянной, может переходить из одних видов в другие.
При действии неконсервативных сил возможен переход механической энергии в другие немеханические виды энергии. В этом случае справедлив более общий закон сохранения:
ОПРЕДЕЛЕНИЕ: в изолированной от любых внешних воздействий системе остается постоянной сумма всех видов энергии (включая и немеханические).
К этому добавим, что в природе и технике постоянно имеют место превращения энергии из одних видов в другие. Проиллюстрируем это таблицей.
Все формулы
Все формулы по физике и математике
Темы по физике
- Механика (56)
- Кинематика (19)
- Динамика и статика (32)
- Гидростатика (5)
- Молекулярная физика (25)
- Уравнение состояния (3)
- Термодинамика (15)
- Броуновское движение (6)
- Прочие формулы по молекулярной физике (1)
- Колебания и волны (22)
- Оптика (9)
- Геометрическая оптика (3)
- Физическая оптика (5)
- Волновая оптика (1)
- Электричество (39)
- Атомная физика (15)
- Ядерная физика (3)
Темы по математике
- Квадратный корень, рациональные переходы (1)
- Квадратный трехчлен (1)
- Координатный метод в стереометрии (1)
- Логарифмы (1)
- Логарифмы, рациональные переходы (1)
- Модуль (1)
- Модуль, рациональные переходы (1)
- Планиметрия (1)
- Прогрессии (1)
- Производная функции (1)
- Степени и корни (1)
- Стереометрия (1)
- Тригонометрия (1)
- Формулы сокращенного умножения (1)
Потенциальная энергия упруго деформированного тела
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДАПотенциальная энергия упруго деформированного тела — физическая величина, равная половине произведения жесткости тела на квадрат его деформации.
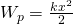
Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к не растянутому состоянию, то есть найдем упругую энергию растянутой пружины.

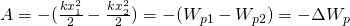
Потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, то есть чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы.
Потенциальная энергия :
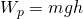
Кинетическая энергия
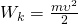
Тут мы использовали :
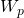 — Потенциальная энергия упруго деформированного тела
— Потенциальная энергия упруго деформированного тела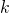 — Коэффициент упругости пружины
— Коэффициент упругости пружины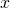 — Деформация пружины
— Деформация пружины

