Структурная схема рычажного механизма

Структурная схема рычажного механизма

Лабораторная работа № 1.

Структурный и кинематический анализ рычажных механизмов.

Цель и задачи работы : изучение основных положений и принципов структурного анализа плоских рычажных механизмов; знакомство с правилами составления структурных схем механизмов, условными обозначениями их элементов по ГОСТ-2.770-68, классификацией механизмов по Ассуру; проведение структурного анализа для заданного рычажного механизма, проверка правильности выполненного анализа на ЭВМ.

Основные положения и понятия структурного анализа механизмов.Механизм — система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел. Звено — твердое тело или система жестко связанных твердых тел, входящая в состав механизма. Все механизмы можно рассматривать как пространственные. Некоторые механизмы можно рассматривать и как плоские. Плоским называется механизм, звенья которого совершают движения в плоскостях, параллельных какой-либо одной плоскости. Движения звеньев механизма рассматривается в системе координат, связанной с одним из звеньев механизма. Это звено называется стойкой и принимается за неподвижное. Входное звено — звено, которому сообщается исходное движения; выходное — выполняет требуемое движение. Соединение двух соприкасающихся звеньев, допускающее их вполне определенное относительное движение, называется кинематической парой.

Кинематические пары классифицируются по следующим признакам:

виду контакта звеньев — на высшие (с контактом звеньев по линии или точке), и низшие (с контактом звеньев по поверхности);

характеру относительного движения звеньев. Низшие КП подразделяются на вращательные, поступательные и винтовые;

числу связей, наложенных КП на относительное движение звеньев (КП 1. 5 классов);

числу подвижностей в относительном движении звеньев КП — на кинематические пары с 1. 5 подвижностями.

Например, вращательная и поступательная КП являются низшими одноподвижными парами 5-го класса.

При проведении теоретических и экспериментальных исследований пользуются различными расчетными схемами и моделями механизмов и машин. Они обычно отражают только те свойства механизмов и машин, которые существенно влияют на исследуемые характеристики. Так, при анализе структуры механизма используют его структурную схему; при анализе кинематики — кинематическую; динамики — динамическую. Структурная схема механизма должна содержать информацию о числе его звеньев и их взаимном расположении, виде расположении и классе (или числе подвижностей) кинематических пар. Структурную схему механизма вычерчивают по определенным правилам с использованием условных обозначений, регламентированных ГОСТ 2.770-68. Некоторые обозначения, необходимые для выполнения данной работы, приведены в табл.1.1.

Графическое изображение элементов структурных схем

Функциональные возможности механизма, в первую очередь, обусловлены числом подвижностей W , т.е. числом независимых обобщенных координат, однозначно определяющих положение всех звеньев механизма в пространстве. При подсчете W можно рассматривать механизм как пространственный и использовать формулу Сомова- Малышева:

W _пр = (1.1)

где n=(k-1) — число подвижных звеньев механизма; k — общее число звеньев (вместе со стойкой); i — число подвижностей в КП; p_i — число КП с i подвижностями в механизме.

Если движение звеньев механизма происходит в параллельных плоскостях, то его можно рассматривать как плоский. В этом случае подвижность определяют по формуле Чебышева:

W _пл =. (1.2)

При расчете подвижности механизма в пространстве необходимо учитывать, что при переходе от плоского представления механизма к пространственному число подвижностей каждого звена увеличивается с трех до шести. При этом подвижность некоторых пар может увеличиться. Так в плоском механизме сферические и цилиндрические пары относятся к одноподвижным низшим. В пространственном они становятся: сферическая – трехподвижной, цилиндрическая – двухподвижной.

Большинство механизмов, применяющихся в современных машинах, имеет одну подвижность. При этом достаточно задать движение одному звену для осуществления вполне определенного движения всех остальных. Механизм с W>1 используют реже. Для многих механизмов при расчете по формуле (1.1) получают отрицательное значение или нуль. Однако анализ движения рассматриваемого механизма показывает, что число его подвижностей равно единице. Такое расхождение возникает, если в схеме механизма имеются повторяющиеся или избыточные связи.

Избыточными называют такие связи в механизме, которые дублируют уже имеющиеся и не изменяют его реальной подвижности. Их вводят в структуру механизма с целью повышения его жесткости и точности. Число избыточных связей q в механизме можно определить после задания его подвижности W₀ (часто W=1):

Величина q определяет степень статической неопределимости механизма при силовом расчете.

1.2. Классификация рычажных механизмов по Ассуру.

Для плоских механизмов с низшими КП Ассуром Л.В. была разработана система классификации, в которой механизмы состоят из первичных механизмов и структурных групп Ассура (групп нулевой подвижности). Первичным механизмов (рис.1) называют механизм, состоящий из двух звеньев: 1, 0 (одно из них неподвижное — стойка), которые образуют одноподвижную пару (вращательную или поступательную).

Структурная группа, или группа Ассура — кинематическая цепь, которая состоит из подвижных звеньев, соединенных между собой низшими одноподвижными КП, и имеет число подвижностей группы (на плоскости), равное нулю. Звено группы Ассура, входящее в две кинематические пары, одна из которых имеет свободный элемент звена (табл.1.2, пунктирные линии), называется поводком. При синтезе механизма группа присоединяется поводками к звеньям исходного механизма. Если поводки группы присоединить свободными элементами КП к стойке, то образуется плоская статически определимая ферма q _гр пл =0 и

Из выражения (1.4) получают соотношение между числом звеньев и числом КП для групп Ассура n _гр =(2/3)p _гр. При решении этого уравнения в целых числах определяют параметры групп Ассура: 1-го класса 2-ого порядка — n _гр =2, p _гр =3 (двухповодковые группы); 1-го класса 3-ого порядка — n _гр =4, p _гр =6 (трехповодковые группы) и т.п.

Сложная группа Ассура не может быть образована комбинацией простых групп более низкого класса или порядка. Некоторые примеры групп Ассура 1-го класса 2-го и 3-го порядков приведены в табл.1.2.

При структурном анализе механизма по Ассуру находят количество первичных механизмов и звенья, образующие их, вид и класс групп Ассура, входящих в его состав. Число первичных механизмов, входящих в состав анализируемого механизма, равно подвижности W _пл. После выделения звеньев, образующих первичные механизмы, определяют состав и вид групп Ассура, анализируя оставшиеся звенья, начиная со звеньев, наиболее удаленных от первичных механизмов. Звенья объединяют в группу Ассура и мысленно удаляют ее из схемы механизма. При этом оставшиеся звенья образуют механизм с тем же числом подвижностей W _пл и не изменяют характера своего движения.

Структурные группы Ассура.

Группы Ассура 1-го класса 2-го порядка (2-го класса 2-го порядка)*

Структурный анализ плоского рычажного механизма

Структурная схема механизма

Рисунок 1.1 — Структурная схема механизма

Таблица 1 — Звенья механизма

Структурная схема механизма состоит из пяти подвижных звеньев и неподвижной стойки, представленной шарнирно-неподвижной опорой и двумя направляющими ползунов 3 и 5.

Подвижность механизма

Подвижность механизма определяем по формуле Чебышева:

где W — подвижность механизма;

n — число подвижных звеньев;

p₅ и p₄ — соответственно число пар пятого и четвертого класса.

Для определения значений p₄ и p₅ найдем все кинематические пары, входящие в состав рассматриваемой кинематической цепи. Результаты исследования заносим в таблицу 1.

Таблица 2 — Кинематические пары

Из анализа данных (таблица 2) следует, что исследуемая схема кривошипно-ползунного механизма представляет собой замкнутую кинематическую цепь и состоит из семи пар пятого класса, пар четвертого класса в составе структуры нет. Следовательно, p₅=7, а p₄=0.

Подставив найденные значения n, p₄ и p₅ в формулу (1), получим:

Полученный результат означает, что для однозначного описания положения всех звеньев механизма в рассматриваемой плоскости достаточно знать одну обобщенную координату ц₁.

Анализ состава структуры механизма

Для решения данной задачи используется структурная классификация механизмов, предложенная профессором Ассуром, согласно которой плоские рычажные механизмы состоят из структурных групп звеньев и первичных (элементарных) механизмов.

Начиная с выходных звеньев — ползунов 3 и 5, разбиваем рассматриваемую схему кривошипно-ползунного механизма на группы звеньев. При этом руководствуемся следующим правилом: если выделенная группа звеньев обладает совместно нулевой подвижностью, то эта группа звеньев является структурой группой Ассура (СГА).

Количество подвижных звеньев определяет класс СГА.

Поводок — это конечное звено СГА, входящее в состав кинематической пары и имеющее свободный элемент звена.

Количество поводков определяет порядок группы, а вид СГА определяется ее структурной схемой.

Рассмотрим группу звеньев 2-3 (рисунок 1.2).

Рисунок 1.2 — Группа звеньев 2-3

Данная группа состоит из двух подвижных звеньев: шатун 2 и ползун 3, и трех кинематических пар:

1-2 вращательная пара пятого класса;

2-3 вращательная пара пятого класса;

3-0 поступательная пара пятого класса.

Следовательно, структурная формула — ВВП, являющаяся вторым видом.

Поводки представлены звеном 1 и направляющей ползуна.

Подставив выявленные значения в формулу (1), получим:

Следовательно, группа звеньев 2-3 является структурной группой Ассура второго класса, второго порядка, второго вида.

Рассмотрим группу звеньев 4-5 (рисунок 1.3).

Рисунок 1.3 — Группа звеньев 4-5

Данная группа состоит из двух подвижных звеньев: шатун 4 и ползун 5, и трех кинематических пар:

1-4 вращательная пара пятого класса;

4-5 вращательная пара пятого класса;

5-0 поступательная пара пятого класса.

Следовательно, структурная формула — ВВП, являющаяся вторым видом.

Поводки представлены звеном 1 и направляющей ползуна.

Подставив выявленные значения в формулу (1), получим:

Следовательно, группа звеньев 4-5 является структурной группой Ассура второго класса, второго порядка, второго вида.

Рассмотрим группу звеньев 0-1 (рисунок 1.3).

Рисунок 1.3 — Группа звеньев 0-1

Данная группа состоит из подвижного звена кривошипа 1, стойки 0 и одной кинематической пары (вращательная 0-1)

Подставив найденные значения в формулу (1), получим:

Следовательно, группа звеньев 0-1 не является структурной группой Ассура, а представляет собой первичный механизм, подвижность которого равна единице, т.е. существует одна обобщенная координата.

Из проведенного анализа следует, что число степеней свободы механизма равно единице; механизм имеет следующий структурный состав (рисунок 1.4): первичный механизм с подвижностью равной единице и две структурные группы Ассура второго класса, второго порядка, второго вида.

Рисунок 1.4 — Структурный состав кривошипно-ползунного механизма

Вывод: подвижность механизма определяется подвижностью первичного механизма, входящего в его состав. Класс механизма определяется классом наиболее сложной структурной группы. Рассмотренный механизм является механизмом второго класса.

СОСТАВЛЕНИЕ КИНЕМАТИЧЕСКОЙ СХЕМЫ И СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНЫХ МЕХАНИЗМОВ

Углубление теоретических знаний и приобретение практических навыков по структурному анализу плоских и пространственных рычажных механизмов.

2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Механизм – устройство, предназначенное для преобразования движения одного или нескольких тел в требуемые движения других тел.

Механизм состоит из звеньев подвижных и неподвижных. Звено может состоять из нескольких жестко соединенных деталей. Звено, относительно которого рассматриваются движения всех остальных звеньев, называется неподвижным или стойкой.

По характеру движения подвижные звенья различают: кривошип – звено, делающее полный оборот вокруг неподвижной оси; коромысло – звено, совершающее колебательные движения; ползун – звено, совершающее возвратно-поступательное движение; кулиса – звено, являющееся подвижной направляющей другого звена, называемого кулисным камнем.

Подвижное соединение двух звеньев, находящихся в соприкосновении, называется кинематической парой. Поверхности, линии или точки, по которым происходит соприкосновение звеньев, образующих кинематическую пару, называются элементами звеньев. Если элементами звеньев, образующих пару, является поверхность, то такая кинематическая пара называется низшей (в таблице все пары низшие); если же – линия или точка, то кинематическая пара называется высшей (шар или цилиндр на плоской поверхности, соприкосновение любых цилиндрических поверхностей по образующим). Условное обозначение кинематических пар приведено в таблице.

Кинематические пары накладывают на относительные движения звеньев, образующих пару, ограничения (условия связи). Максимальное условие связей S, накладываемых кинематической парой, равно 5 (в случае S=6 соединение двух звеньев будет неподвижным). По числу условий связи S кинематические пары делятся на 5 классов. В таблице приведены конструктивные оформления и условные изображения наиболее встречающихся на практике кинематических пар.

Совокупность звеньев, образующих между собой кинематические пары, называют кинематической цепью. Кинематическая цепь может быть плоской и пространственной. Если точки звеньев кинематической цепи в относительном движении перемещаются в параллельных плоскостях, то такая кинематическая цепь плоская, в противном случае пространственная.

Механизм может быть определен как кинематическая цепь с одним неподвижным звеном (стойкой). По аналогии с кинематическими цепями механизмы могут быть плоскими и пространтвенными. Число степеней свободы кинематической цепи относительно неподвижного (стойки) называется степенью подвижности механизма. Для пространственного механизма без избыточных связей степень подвижности определяется по формуле Малышева

(1)

где n – число подвижных звеньев; р_i – число кинематических пар i-го класса; i – номер класса кинематической пары.

Степень подвижности плоских механизмов определяется по формуле Чебышева

(2)

где n – число подвижных звеньев; р₅ – число кинематических пар 5-го класса; р₄ – число кинематических пар 4-го класса.

Звено механизма, закон которого задан, называется входным, звено, при получении движения которого предназначен механизм, называется выходным. Входное (выходное) звено со стойкой называется исходным механизмом (рис. 1).

По Л.В. Ассуру любой механизм может быть получен путем последовательного присоединения к исходному механизму групп звеньев с степенью подвижности относительно к присоединенным звеньям. Такие группы звеньев называются структурными, или группами Ассура (рис. 2).

Структурные группы делятся на классы и имеют порядок. Класс груп определяется числом кинематических пар, входящих в наиболее сложный замкнутый контур групп. Порядок групп определяется числом свободных кинематических пар, которыми группа присоединяется к механизму (см. рис. 2).

W=1 W=2 W=3

СОСТАВЛЕНИЕ СХЕМ И СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНЫХ МЕХАНИЗМОВ

1. Создание жидкокристаллического дисплея

2. Характеристики ЖК мониторов

3. Виды ЖК мониторов

4. Разрешение монитора

5. Интерфейс монитора

6. Тип ЖК матрицы

7. Классификация TFT-LCD дисплеев

11. Особенности различных ЖК матриц

15. Время реакции пикселя

16. Количество отображаемых цветов

СОСТАВЛЕНИЕ СХЕМ И СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНЫХ МЕХАНИЗМОВ

Цель работы заключается в изучении строения (структуры) конкретного механизма, заданного студенту в виде некоторой модели.

1.1. Основные сведения о строении механизмов

Механизм состоит из отдельных звеньев. Звеном называется жесткая деталь или несколько деталей, жестко связанных между собой и совершающих одно движение. Все неподвижные детали образуют неподвижное звено, или стойку. У одного механизма может быть только одна стойка. Подвижные звенья бывают входными (ведущими) и выходными (ведомыми). Звено, которому сообщается движение, называется входным. Звено, которое осуществляет требуемое движение, для которого предназначен механизм, называется выходным. Начальным называют звено, координаты которого являются обобщенными для данного механизма, т. е. определяют движение всех остальных звеньев (чаще всего за начальное принимают входное звено).

Кинематической парой называется соединение двух звеньев, имеющих относительное движение между собой. Кинематические пары классифицируются по трем признакам:

1) по характеру соприкосновения звеньев;

2) по характеру относительного движения звеньев,

3) по числу наложенных на относительное движение условий связи.

При классификации кинематических пар механизм надо представить реально.

По первому признаку кинематические пары делятся на высшие и низшие. Если контакт звеньев точечный или линейный, то кинематическая пара является высшей, а если соприкосновение звеньев происходит по любой поверхности – низшей.

По характеру относительного движения звеньев кинематические пары делятся на плоские и пространственные. Если движение звеньев происходит в одной или параллельных плоскостях, то пара называется плоской, в противном случае – пространственной.

По числу s наложенных на относительное движение условий связи пары делятся на пять классов. Класс кинематической пары определяется числом наложенных связей, вычисленных по формуле:

где 6 – число независимых движений свободного тела; Н – число оставшихся степеней свободы.

Для нахождения движения одного звена относительно другого необходимо отбросить внешние связи, оставив только эти два звена, и выбрать удобную систему координат. Затем одно из звеньев мысленно представляется неподвижным и определяется число независимых движений, которые имеет подвижное звено относительно неподвижного.

В качестве примера рассмотрим определение класса кинематической пары цилиндр – плоскость (рис. 1.1). При неподвижной плоскости цилиндр может иметь четыре относительных движения: два вращательных и два поступательных. Он не может вращаться вокруг оси Оу, так как нарушается линейный контакт, и не может перемещаться вдоль оси Oz, так как распадается связь (цилиндр отрывается от плоскости). В этом случае пара является парой II класса, так как число наложенных связей .

Условные обозначения некоторых кинематических пар показаны на рис. 1.2.

Рис. 1.2. Условные обозначения и класс кинематических пар

Система звеньев, соединенных между собой кинематическими парами, называется кинематической цепью.

Механизмом называется кинематическая цепь с одним неподвижным звеном, в которой заданному движению одного или нескольких звеньев соответствуют вполне определенные движения всех остальных звеньев.

Одной из основных задач структурного анализа механизма является определение числа степеней свободы и класса механизма. Для решения этих задач составляется структурная схема механизма. Конструктивные элементы звеньев, а также звенья и их связи, не оказывающие влияния на движение механизма, при структурном анализе на схеме не показываются. Так, на рис. 1.3,а ролик 3 создает избыточную степень свободы, он служит только для уменьшения трения, а на рис. 1.3,б звено 3 накладывает пассивное (избыточное) условие связи, увеличивая жесткость механизма (конструкции). В обоих случаях звенья 3 не изменяют законов движения выходных звеньев 2.

Степень свободы (степень подвижности) плоского механизма определяется по формуле академика П.Л. Чебышева:

где n – число подвижных звеньев; p₄, p₅ – число кинематических пар соответственно четвертого и пятого класса.

Степень подвижности W показывает число независимых движений, которые надо задать механизму для получения определенности движения всех его звеньев.

Группой Ассура называется простейшая незамкнутая кинематическая цепь с нулевой степенью подвижности. Она не изменяет степени подвижности основного механизма (1-го класса) после присоединения к нему. Таковой является система двух звеньев АВО₂ на рис. 1.4.

Для группы Ассура

При структурном анализе плоских механизмов с высшими кинематическими парами IV класса их заменяют на низшие кинематические пары V класса. Каждая высшая кинематическая пара заменяется двумя низшими и дополнительным звеном. Тогда

и, следовательно

Так как n и р₅ могут быть только целыми числами, то число звеньев n в группе Ассура должно быть четным, а число пар пятого класса р₅ – кратно трем.

Простейшие группы Ассура состоят из двух звеньев, образующих между собой и с другими звеньями механизма три кинематические пары (рис. 1.4). Присоединив такую группу внешними парами А и О₂ к кривошипу 1 и к стойке О (рис. 1.5), получим четырехзвенный механизм О₁АВО₂ (рис. 1.6).

По классификации Л.В. Ассура – И.И. Артоболевского класс группы Ассура определяется числом кинематических пар, образующих наиболее сложный замкнутый контур. Если замкнутый контур отсутствует, то выбирается звено с наибольшим числом кинематических пар. Так, группа Ассура на рис. 1.4 является группой II класса, а на рис. 1.7 – III класса.

Порядок группы Ассура определяется числом кинематических пар, которыми группа присоединяется к имеющемуся механизму. Эти пары называются внешними.

Группы Ассура II класса второго порядка подразделяются на пять видов в зависимости от числа и расположения вращательных и поступательных пар. Наиболее часто встречающиеся виды показаны на рис 1.8.

Примеры групп Ассура различных классов и порядков представлены на рис.1.9.

Класс механизма определяется классом наиболее сложной группы Ассура. Знание класса механизма позволяет выбрать соответствующий метод кинематического и кинетостатического исследования данного механизма.

По классификации Л.В. Ассура – И.И. Артоболевского простейший двухзвенный механизм состоит из одного подвижного входного звена, например кривошипа 1, и стойки О, соединенных одной низшей кинематической парой V класса О₁ (рис. 1.5). Такой механизм называется механизмом I класса (первичным механизмом) и степень его подвижности равна единице:

Более сложные механизмы образуются присоединением к входному звену и стойке групп Ассура, обладающих нулевой степенью свободы. При этом число степеней свободы механизма W не изменяется.

Рассмотрим образование механизма на конкретном примере (рис. 1.10). К входному звену 1 и стойке О сначала присоединяется группа Ассура II класса, состоящая из двух звеньев 2, 3 и кинематических пар А,В,О₂, образуя механизм О₁АВО₂. Затем присоединяется другая группа Ассура также II класса, состоящая из звеньев 4, 5 и кинематических пар D,E,F, образуя более сложный механизм О₁АВО₂ DEF.

Формула строения механизма имеет вид:

Рассмотренный в предыдущем примере механизм является механизмом II класса, так как обе присоединенные группы Ассура – группы II класса.

Класс механизма зависит от того, какое из звеньев является входным. Так, при входном звене 1 механизм на рис. 1.11 имеет одну группу Ассура III класса и принадлежит к III классу механизмов. При входном звене 5 это будет уже механизм II класса, образованный звеньями 1, 2 с кинематической парой А,В,О₁ и звеньями 3, 4 с кинематическими парами D,C,O₂.

В процессе структурного анализа механизма от него последовательно отсоединяются группы Аcсура, причем сначала отсоединяется группа, наиболее удаленная от входного звена. После отсоединения всех групп Ассура остаются входное звено и стойка. Отсоединение группы Ассура не изменяет степени подвижности оставшейся части механизма, то есть движение звеньев остается неизменным.

При выполнении структурного анализа в первую очередь отсоединяются простейшие группы Ассура II класса, состоящие из двух звеньев и трех кинематических пар. Если это невозможно, то отсоединяются более сложные кинематические цепи с нулевой степенью свободы. При этом надо помнить, что в группах Ассура всегда четное число звеньев, а число кинематических пар кратно трем.

Выполняя структурный анализ, необходимо иметь в виду, что входное звено и стойка не входят в группу Ассура, а каждое звено и каждая кинематическая пара входят только в одну группу Ассура.

1.2. Порядок выполнения лабораторной работы

1. Ознакомиться с механизмом, установить его назначение (например, преобразование вращательного движения в поступательное), определить число звеньев и кинематических пар.

2. Вычертить структурную схему механизма, направление движения входного звена показать стрелкой.

3. Пронумеровать звенья арабскими цифрами в порядке их присоединения к входному звену. Кинематические пары обозначить прописными буквами латинского алфавита. Кинематические пары со стойкой обозначаются, как правило, через О₁, О₂, О₃…

4. Составить таблицу кинематических пар, в которой произвести их классификацию по трем признакам (см. табл. 1.1).

Структурный анализ рычажного механизма

Механизм штамповочной машины состоит:

Механизм штамповочной машины состоит из 7-ми кинематических пар:

I. Стойка 0 – кривошип 1 (вращательная пара 5 класса)

II. Кривошип 1- шатун 2 (вращательная пара 5 класса)

III. шатун 2 –коромысло 3 (вращательная пара 5 класса)

IV. коромысло 3 – стойка 6 (вращательная пара 5 класса)

V. коромысло 3 – шатун 4 (вращательная пара 5 класса)

VI. Шатун 4 –ползун 5 (вращательная пара 5 класса)

VII. ползун 5 – направляющая (поступательная пара 5 класса)

Степень подвижности механизма определяется по формуле П.Л. Чебышева

где n- число подвижных звеньев (n=5);

p₅ – число кинематических пар 5 го класса (p₅ = 7);

p₄ — число кинематических пар 4 го класса (p₄=0).

Таблица групп Ассура:

Таблица механизмов 1 класса:

Формула строения механизма:

Таким образом, данный механизм, является механизмом 2 го класса.

Проектирование рычажного механизма

Определяем размеры звеньев.

Дано: ,

0.0025м/мм

Рассмотрим подобные треугольники и :

= ;

Окружность L является геометрическим местом точек центра вращения кривошипа. Любая точка, взятая на этой окружности, обеспечит заданный угол . Если не вводить дополнительных усилий, то задача имеет множество решений.

Ставим на чертеже точку D. Далее из т.D проводим горизонтальную прямую и откладываем угол вверх и вниз от горизонтали. Затем проводим отрезки DB и DB₁(крайние положения коромысла). Соединяем точки B и B₁. От точки B откладываем прямой угол а от точки В₁ — . Вокруг полученного прямоугольного треугольника проводим окружность L и ставим точку O. Из точки O проводим окружность радиусом . Делим ее на 12 частей и методом засечек находим положения остальных точек. Длину шатуна СЕ выбираем произвольно = 0,4м.

Определение скоростей точек звеньев и угловых скоростей звеньев методом планов

Скорость точек можно определить методом планов скоростей. Кинематические исследования этим методом производятся в следующей последовательности:

Рассмотрим построение плана скоростей для 1- го положения механизма:

Найдём угловую скорость кривошипа ( ):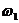

Находим скорость точки А:

Откладываем вектор скорости , ( ) направлен из полюса Р перпендикулярно кривошипу АВ в сторону вращения угловой скорости кривошипа.

Откладываем этот вектор в масштабе:

Составляем векторные уравнения:

Найдем скорость точки B.

Составим для нее систему векторных уровней:

Из точки, на плане скоростей, проведем прямую перпендикулярно ВС это линия действия скорости V_АВ, а из полюса (P) проведем прямую перпендикулярно DB, линия действия скорости V_В. Они пересекаются в т b из полюса проведем в эту точку прямую это, и будет скорость т. В.

Находим скорость движения т.С:

Далее определим скорость точки E, используя следующую систему векторных уравнений:

Из полюса проводим линию действия т.e перпендикулярно СЕ,а из т.d проводим скорость звена СE перпендикулярно этому звену. И на пересечении с линией действия скорости т.E получаем скорость т.E:

Определяем скорости точек S₂ и S₄.

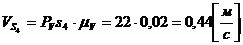
Аналогично строим планы положений для остальных 11 положений механизма.

Угловые скорости находим из выражений:

Полученные результаты сводим в таблицу 1.

Таблица линейных и угловых скоростей

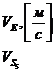
Определение ускорений точек звеньев методом планов

Ускорения точек звеньев и угловые ускорения звеньев находим для заданного 3- го положения механизма ( )

Определяем ускорение точки А предварительно записав векторное уравнение:

т.к. кривошип вращается с постоянной угловой скоростью. Тогда:

Выберем масштабный коэффициент:

Из произвольно выбранного полюса откладываем вектор параллельно OA от A к O.

Далее запишем векторное уравнение для точки B:

где

;

На плане ускорений из точки , откладываем нормальное ускорение звена ВА с учетом параллельно ВА по направлению то точки В к точке А. Далее проводим линию перпендикулярно , а из полюса — параллельно звену ВА плана положений механизма. При пересечении двух прямых ставим точку . Ускорение точки В:

Найдем ускорение нормальное звена ВD:

На плане ускорений откладываем параллельно BD из полюса .

Ускорение точки С найдем из правила подобия. На векторе откладываем .

Ускорение точки Е получим при пересечении направляющей, проведенной из полюса и линии перпендикулярной СЕ.

.

Ускорение точек S₂ и S₄ определяем из следующих условий:

Точки S₂ S₄ находятся на середине звеньев АВ и СЕ, соответственно на плане ускорений они будут тоже расположены посередине и равны: .

Тангенциальные ускорения, а также угловые ускорения найдем из следующих уравнений:

Дата добавления: 2018-02-15 ; просмотров: 176 ; ЗАКАЗАТЬ РАБОТУ

Алгоритм структурного анализа механизма;

Распространение принципа Ассура на рычажные механизмы с внутренними входами (второго типа)

До недавнего времени в теории механизмов принято было считать, что принцип Ассура относится только к рычажным механизмам первого типа, так как механизм второго типа невозможно разделить на начальный механизм и группы Ассура. Отсюда делался вывод о том, что на механизмы второго типа не может быть распространена структурная классификация Ассура.

Однако можно изменить трактовку принципа Ассура таким образом, что он окажется пригодным и для рычажных механизмов второго типа. Это позволит распространить на них структурную классификацию, а также методы и алгоритмы кинематического анализа, разработанные для механизмов первого типа.

Рассмотрим структурную схему какого-либо рычажного механизма второго типа. Проделаем со схемой следующую операцию (выполняемую в два этапа):

1. Ликвидируем относительную подвижность двух звеньев, образующих входную пару;

2. Отбросим стойку.

В результате первого этапа два упомянутых звена объединяются в одно.Назовем это звеноусловным звеном и обозначим через У.

Далее будем рассматривать наиболее распространенный на практике случай, когда в механизмах второго типа входная пара является поступательной. Она образуется двумя звеньями — цилиндром и поршнем, которые в свою очередь образуют вращательные пары (шарниры) со смежными звеньями, причем ось входной поступательной пары проходит через центры двух указанных шарниров. В этом случае условное звено У имеет вид стержня, присоединяемого к двум смежным звеньям при помощи шарниров, расстояние между которыми будем считать длиной звена У и обозначать через L_у. Условное звено имеет переменную длину, поскольку:

где S – обобщенная координата механизма

(перемещение поршня по отношению к цилиндру);

После выполнения двух указанных выше этапов вместо механизма второго типа получается кинематическая цепь, состоящая из (n – 2) звеньев. Эту цепь называют ведомой цепьюмеханизма второго типа.

Отметим, что при проведении указанной операции применительно к механизму первого типа мы придем к такому же результату, как и при отделении от него начального механизма, т.е. получим ведомую цепь механизма.

Общим свойством ведомых цепей механизмов первого и второго типов является то, что каждая такая цепь или является группой Ассу­ра, или может быть разделена на несколько групп Ассура. Отличие же их друг от друга заключается в том, что ведомая цепь механизмов вто­рого типа содержит условное звено У, а у ведомой цепи механизмов первого типа такого звена нет.

Описанный выше единый способ получения ведомой цепи представ­ляет собой основную идею модифицированного принципа Ассура, при­годного для рычажных механизмов, как первого, так и второго типа.

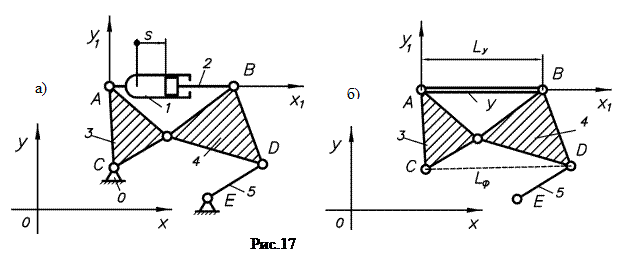
На рис.15а, 16а, 17а приведены в качестве примера схемы трех шестизвенных рычажных механизмов второго типа, у которых входная пара является поступательной и образуется подвижными звеньями 1 и 2— цилиндром и поршнем.

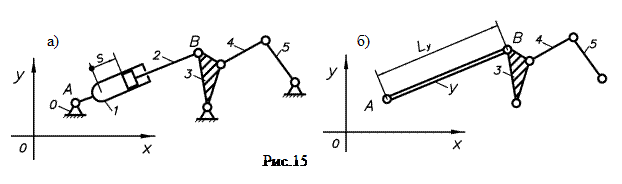
Задано относительное перемещение поршня 2 по отношению к цилиндру 1. Номера других звеньев: 0 — стойка; 3,4,5— подвижные звенья. На рис.15б, 16б, 17б показаны ведомые цепи рассматриваемых механизмов. При этом условное звено — У.

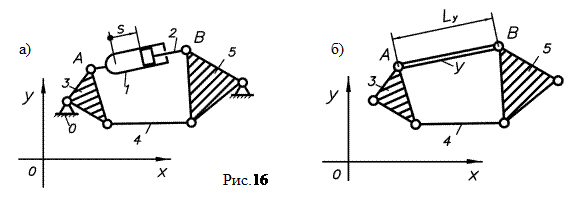
Среди механизмов второго типа встречаются два рода механизмов, различающихся способом формирования групп Ассура из звеньев ведомой цепи.

К механизмам первого рода относятся такие рычажные механиз­мы второго типа, у которых звено У входит в состав первой по номе­ру группы Ассура среди групп, образующих ведомую цепь механиз­ма.

Если же звено У не входит в состав указанной группы, то такие механизмы относятся к механизмам второго рода.

Отметим, что ну­мерация групп Ассура производится в порядке их наслоения (в этом же порядке в последующем производится кинематический анализ механизма).

Особенность структуры рычажных механизмов второго типа второ­го рода состоит в том, что часть звеньев ведомой цепи таких механиз­мов не имеет относительной подвижности по отношению к звену У.

Эти звенья образуют кинематическую цепь, которую будем называть подцепьюведомой цепи.

Нетрудно показать, что подцепь является группой Ассура или состоит из нескольких групп Ассура. Звенья под­цепи вместе со звеном У образуют одно звено, которое будем называть фиктивным звеном(Ф).

Рассмотрим теперь кинематическую цепь, состоящую из звена Ф и звеньев ведомой цепи, не участвовавших в формировании звена Ф.

Эту цепь будем называть фиктивной ведомой цепьюмеханизма.

Последняя или является группой Ассура, или ее можно разделить на несколько групп Ассура, причем первой из них по номеру (в порядке наслоения) является группа, содержащая звено Ф. Любое из звеньев подцепи входит в две группы Ассура: во-первых, в группу, входящую в подцепь, и, во-вторых, в группу, содержащую звено Ф.

Среди механизмов второго типа, приведенных на рис.15а, 16а, 17а два первых механизма относятся к первому роду, а третий меха­низм — ко второму роду.

Ведомая цепь первого механизма (см. рис.15б) разделяется на две ди­ады: звенья У и 3входят в первую диаду, звенья 4и 5 — во вторую диаду. Поэтому рассматриваемый механизм есть механизм второго класса.

Ведомая цепь второго механизма (см. рис.16б) представляет собой четырехзвенную группу Ассура четвертого класса второго порядка (см. табл.2), так что второй механизм есть механизм четвертого класса.

Звенья 3 и 4ведомой цепи третьего механизм (см. рис.17б) не имеют относительной подвижности по отношению к звену У и, следовательно, образуют подцепь. Последняя представляет собой диаду. Подцепь вместе со звеном У образует фиктивное звено Ф. В свою очередь, звено Ф вместе со звеном 5 образует фиктивную ведомую цепь, которая представляет собой диаду. Значит, третий механизм (см. рис.17а) есть механизм первого класса.

Структурный анализплоского рычажного механизма состоит в исследовании структурной схемы. Его выполняют в такой последовательности:

1. Найти число nзвеньев механизма (включая стойку);

2. Установить число ркинематических пар, а также вид каждой пары (поступательная или вращательная);

3. Определить число Wстепеней свободы механизма, а также выявить наличие или отсутствие избыточных связей;

4. Указать тип механизма – первый или второй;

5. Для механизмов первого типа указать входное звено (или входные звенья), а для механизмов второго типа указать входную пару;

6. Пронумеровать звенья, приняв такой порядок (при W =1):

a. для механизмов первого типа:0 – стойка; 1 – входное звено; 2, 3. , (n – 1) – другие подвижные звенья;

b. для механизмов второго типа: 0 – стойка; 1 и 2 – два звена, образующих входную пару; 3, 4. , n – другие подвижные звенья;

7. Выделить (n – 2)– звенную ведомую цепь с учетом типа механизма:

c. для механизмов первого типа в ведомую цепь входят звенья 2, 3. , (n – 1);

d. для механизмов второго типа в ведомую цепь входят звенья 3, 4. , (n– 1), а также условное звено У, полученное путем жесткого соединения друг с другом звеньев 1и 2;

8. Для механизмов второго типа установить род механизма – первый или второй;

9. Разделить ведомую цепь на группы Ассура, указать последовательность наслоения групп, установить класс и порядок каждой группы;