Обозначение уклона и конусности на чертежах

Конусность и уклон

На изображениях конических элементов деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина; угол наклона образующей (или угол конуса) или величина конусности и диаметр основания, длина и т.п.

Конусность

Отношение разности диаметров двух поперечных сечений конуса (D-d.) к расстоянию между ними (l) (рис. 6.39, а) называется конусностью (К): К = (D – d)/l.

Рис. 6.39. Построение конусности и нанесение се величины

Например, конический элемент детали с диаметром большего основания 25 мм, диаметром меньшего основания 15 мм, длиной 50 мм будет иметь конусность К = (D – d)/l = (25 – 15)/50 = 1/5 = 1:5.

При проектировании новых изделий применяются величины конусности, установленные ГОСТ 8593–81: 1:3; 1:5; 1:7; 1:8; 1:10; 1:12; 1:15; 1:20; 1:30. Стандартизированы также величины конусности, которые имеют элементы деталей с часто встречающимися углами между образующими конуса: углу 30° соответствует конусность 1:1,866; 45° – 1:1,207; 60° – 1:0,866; 75° – 1:0,652; углу 90° – 1:0,5. В чертежах металлорежущих инструментов часто конусность определяется надписью, указывающей номер конуса Морзе. В этих случаях размеры конических элементов устанавливают по ГОСТ 10079–71 и др.

На чертежах конусность наносят согласно правилам ГОСТ 2.307–2011. Перед размерным числом, определяющим величину конусности, наносят условный знак в виде равнобедренного треугольника, острие которого направлено в сторону вершины конуса.

Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно геометрической оси конического элемента.

Они могут быть проставлены над осью (рис. 6.39, 6) или на полке (рис. 6.39, в). В последнем случае полка соединяется с образующей конуса с помощью линии выноски, заканчивающейся стрелкой.

Уклон

Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.

Рис. 6.40. Определение величины уклона

На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.

Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).

Рис. 6.41. Построение уклонов и нанесение их величин

При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.

Рис. 6.42. Построение линии по заданному уклону

Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.

Обозначение уклона и конусности на чертежах

Поверхности многих деталей имеют различные уклоны. Плоские поверхности деталей, расположенные наклонно, на чертежах часто обозначаются величиной уклона. В задании «Проекционное черчение» именно так и задано ребро жесткости или тонкая стенка детали.

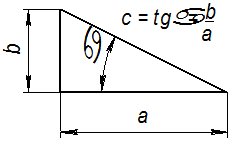
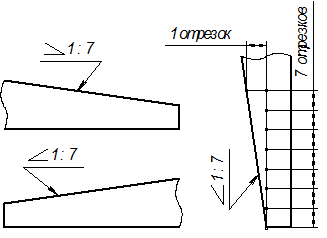
Уклон характеризует отклонение прямой линии или плоскости от горизонтального или вертикального направления. Для построения уклона 1:1 на сторонах прямого угла откладывают произвольные, но равные единичные отрезки. Очевидно, что уклон 1:1 соответствует углу 45º. Как видно из рис. 34,а, уклон есть отношение катетов: противолежащего к прилежащему, что может быть определено как тангенс угла наклона α прямой. Тогда, чтобы, например, построить уклон 1:7 (рис. 34,б), в направлении уклона откладывают семь отрезков, а в перпендикулярном направлении — один отрезок.

Величину наклона обозначают на чертеже в соответствии с ГОСТ 2.307-68 условным знаком с числовым значением. Уклон указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определенной линии: одна из прямых знака должна быть горизонтальной, а другая — наклонена примерно под углом 30º в ту же сторону, что и сама линия уклона (рис. 34,б). Вершина знака должна быть направлена в сторону уклона. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон. На чертеже уклоны указывают либо в процентах, либо дробью в виде отношения двух чисел.

Многие детали содержат коническую поверхность. На чертежах конических деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина, угол конуса или величина конусности.

Конусность — это отношение диаметра основания конуса к его высоте. Для усе­ченного конуса это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (рис. 35,а). Конусность равна удвоенному уклону образующей конуса к его оси. Так же как и уклон, она обозначается условным зна­ком, проставляемым перед её числовым обозначением. Условный знак изобража­ет­ся в виде треугольника с вершиной, направленной в сторону вершины конуса. Конус­ность (согласно ГОСТ 2.307-68) задается на чертежах отношением двух чисел (рис. 35), процентами или десятичной дробью.

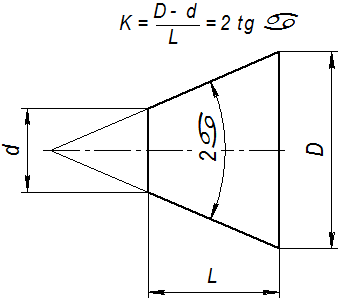
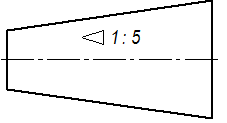
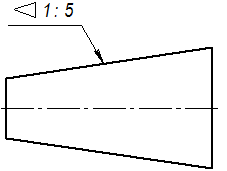
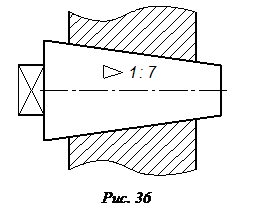
Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно оси конического элемента. Они могут быть расположены над осью, как на рис. 35,б, или полке, как на рис. 35,в. В последнем случае полка соединяется с обра­зующей конуса с помощью линии-выноски, заканчивающейся стрелкой. В кони­чес­ких соединениях, показанных на рис. 36, указание конусности обязательно, так как задание размеров D, d, H из-за трудностей изготовления применяют редко. При построении очертаний конуса, задаваемого конусностью, высотой и одним из диаметров, второй диаметр вычисляют по формуле, приведенной на рис. 35,а. Конусности общего назначения стандартизованы ГОСТ 8593-81.

2. Пример выполнения РГР

На рис. 37 приведен пример варианта задания на выполнение расчетно-графической работы «Проекционное черчение», а также наглядное изображение заданной детали с вырезом.

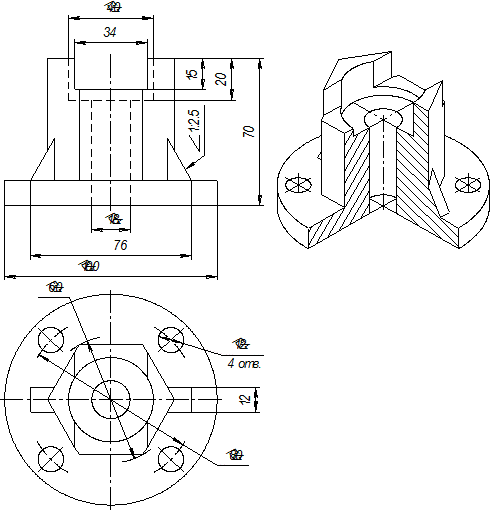
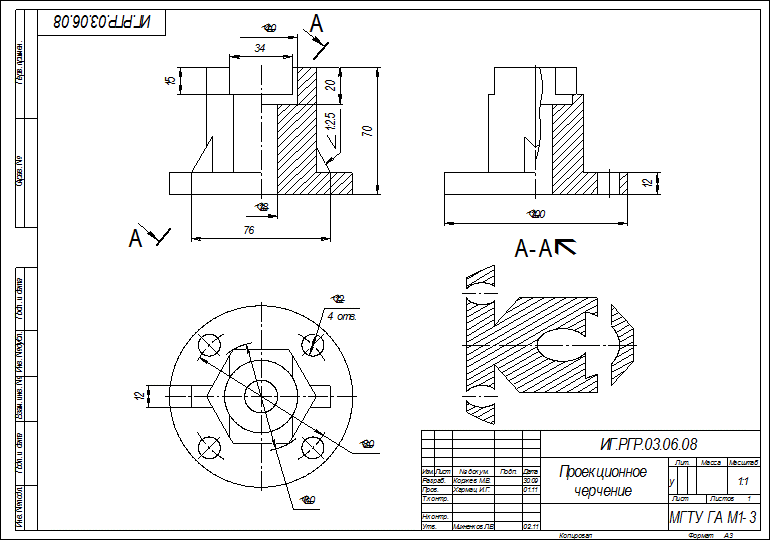
Выполненный по этому заданию чертеж детали в трех проекциях с правильно оформленными размерами показан на рис. 38. Этот при­мер поможет студентам разобраться в их задании, начать выполнение графичес­кой работы и избежать многочисленных ошибок при ее оформлении.

Напомним, что в задании имеются только две проекции детали, поэтому и размеры распределены на двух изображениях. Однако при оформлении чертежа следует наносить размеры равномерно на всех трех проекциях.

В заключение следует отметить, что количество изображений детали (видов, разрезов, сечений) должно быть наименьшим, но обеспечивающим полное пред­став­ление о её конструкции при применении установленных всоответствующих стан­дар­тах условных обозначений, знаков и надписей.

Литература

1. Попова Г.Н., Алексеева С.Ю. Машиностроительное черчение: Справочник. -Л.: Машиностроение, Ленингр. отделение, 1986.

2. Левицкий В.С. Машиностроительное черчение. — М.: Высшая школа, 1988.

3. Гордон В.О., Семенцов-Огиевский Н.А. Курс начертательной геометрии. — М.: Наука, 1994.

4. Фролов С.А. Начертательная геометрия. — М.: Машиностроение, 1978.

Приложение. Варианты задания на расчетно-графическую работу

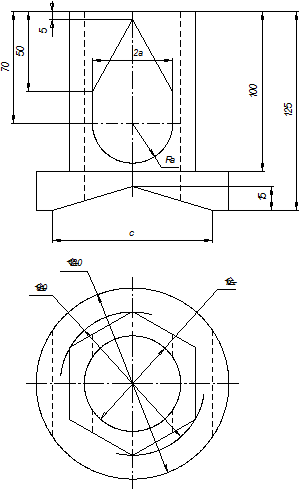
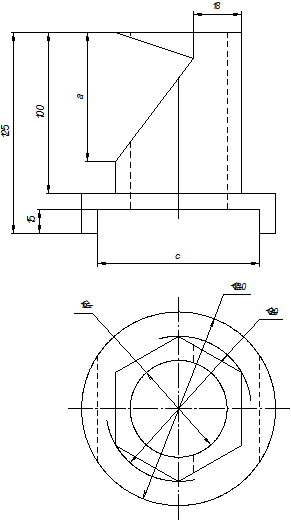
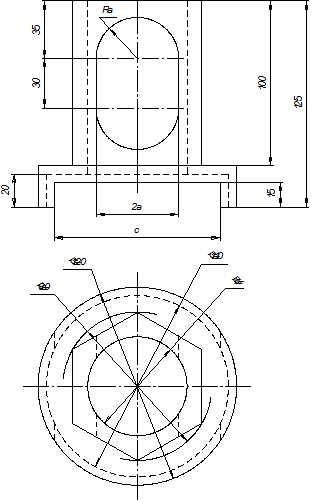
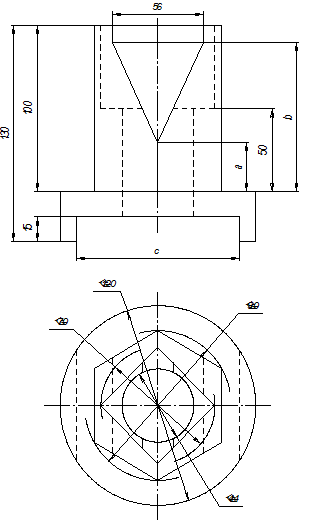
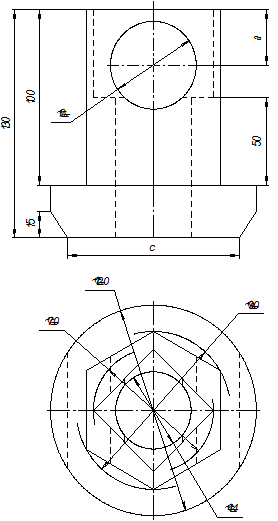
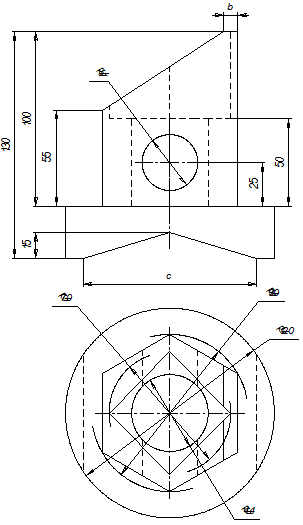
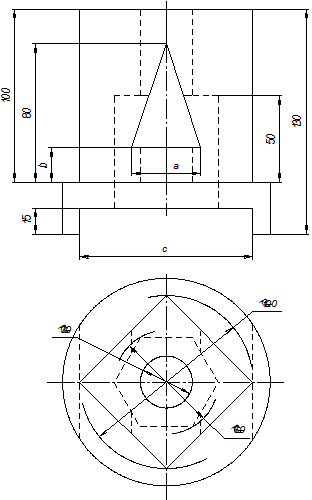
Варианты задания на расчетно-графическую работу по теме «Проекционное черчение» приведены в табл. П1. Правила выбора варианта задания определяются преподавателем.

Таблица П1. Варианты задания на РГР по теме «Проекционное черчение»

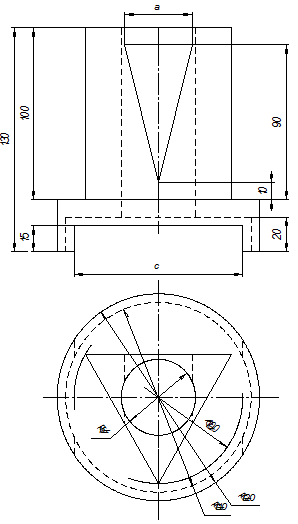
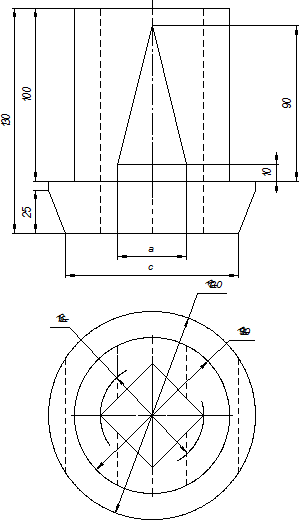
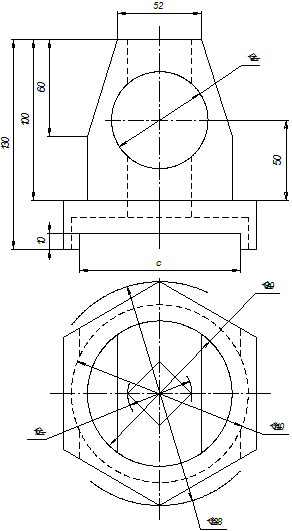
[1] Для вертикальных разрезов указанное требование должно выполняться также в случаях, если секущая плоскость не параллельна фронтальной или профильной плоскости проекции

[2] Условие симметричности изображений необходимо, но не достаточно для совмещения половины вида и половины разреза (подробнее см. подраздел 1.2.3).

Дата добавления: 2014-11-06 ; Просмотров: 3157 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Popular

Основы черчения

Строительное

Машиностроительное

Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:

i=AC/AB=tga

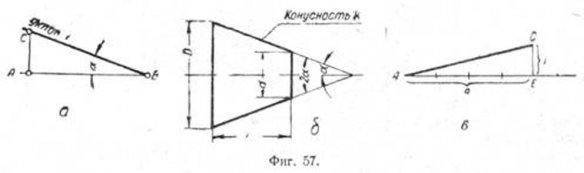
Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)

k=(D-d)/l=2tga

k = 2i

Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.

Например: конусность, выраженная в градусах — 11°25’16″; отношением — 1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38″; отношением — 1:10; дробью—0,1; в процентах — 10%.

Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.

Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):

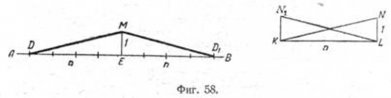
1) построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2) опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

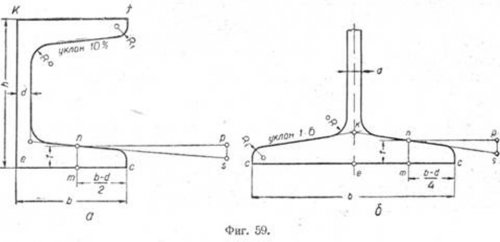
Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм. Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2. В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:

ps/np=10/100,

ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

i=ps/np=1/6

где i — заданный уклон.

Подставив в формулу числовые значения, получим

ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.

от проекта «Инфоурок»

Отдых и оздоровление в экологически чистом
регионе Беларуси для детей 8-17 лет

(всего 59 800 33 300 руб. за 14 дней, 11-24 августа)

Задание: на листе формата А3 выполнить по заданным размерам контур детали с построением уклона, конусности в масштабе 1:1. Нанести размеры

Примечание. Линии построения уклона и конусности сохранить.

В основной надписи указать название деталей в соответствии с вариантом.

— изучить правила оформления чертежей по ГОСТ 2.301-68, ГОСТ 2.302-68; ГОСТ 2.303-68

— изучить правила построения уклона и конусности в соответствии с п.2.40, 2.41 ГОСТ 2.307-68.

— изучить основные правила нанесения размеров на чертежах ГОСТ 2307-68

— приобрести навыки геометрических построений

Методические указания: прежде чем выполнить задание необходимо ознакомиться с п.2.40, 2.41 ГОСТ 2.307-68.

Для получения уклона через заданную точку нужно построить прямоугольный треугольник с одной из вершин в заданной точке К так, как это показано на рис.3.1. Отношение катетов должно соответствовать отношению, указанному в обозначении уклона.

Построение конусности при заданной высоте L и диаметре D одного из оснований можно выполнить графически следующим образом: построить на заданной оси вспомогательный конус, у которого произвольно взятое основание а укладывается в высоте столько раз, сколько задано в обозначении конусности. Затем провести образующие искомого конуса параллельно образующим вспомогательного конуса через концы заданного диаметра, как показано на рис.3.2.

Рис. 3.1- построение уклона

Рис. 3.2- построение конусности

Конусность можно рассчитать по формуле

где D – диаметр основания конуса, l – высота.

Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид:

Обозначение конусности на чертеже

рис. 3.3- обозначение конусности

Варианты заданий к выполнению графической работы

ПОСТРОЕНИЕ УКЛОНОВ И КОНУСНОСТИ

Уклоны .Величина наклона одной прямой по отношению к другой прямой называется уклоном. Уклон выражается тангенсом угла α между этими прямыми.

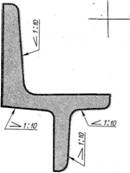
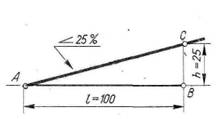Уклоны обычно выражают отношением двух чисел, например 1:3, из которых числитель можно графически изобразить как один из катетов АС прямоугольного треугольника, а знаменатель — как другой катет АВ этого же треугольника .Уклон может быть выражен в процентах, например 25% .

На чертежах обозначение уклона наносят на полке линии-выноски, упирающейся в линию уклона. Полка линии-выноски параллельна линии направления, по отношению к которой задан уклон. Перед числовым значением уклона наносят знак. Вершина угла знака направлена в сторону уклона, а нижняя линия знака параллельна полке линии-выноски. (Рис.1)

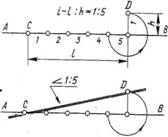Построение уклона. Дан отрезок АВ и на нем точка С. Надо провести прямую с уклоном 1:5 к линии АВ через заданную на ней точку С. От точки С откладывают пять равных отрезков произвольного размера. На перпендикуляре, проведенном из точки 5 к прямой АВ, откладывают один отрезок того же размера, получают точку D. Прямая проведенная через точки С и D будет иметь уклон 1:5 к прямой АВ.(рис.2)

Рис.2

Конусность (рис.3)

Конусностью называется отношение диаметра D основания прямого кругового конуса к его высоте Н.

Для усеченного конуса конусность выражается отношением разности диаметров D и d нормальных сечений кругового конуса к расстоянию между ними . Обозначение конусности наносится на линии-выноске со стрелкой. Перед размерным числом, характеризующим конусность, наносят знак, острый угол которого должен быть направлен в сторону вершины конуса. (рис.3 )

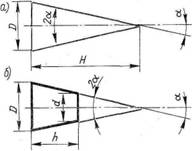
Рис.3

ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАБОТЫ.

Начертите 8 окружностей радиусом 20 мм.

1.2..I Деление на 4 равные части. (рис.4а.). Проведите в окружности 2 взаимно перпендикулярные оси. Эти оси делят окружность на 4 равные части. Соедините точки А,В,С,D) сплошной основной линией, получите вписанный квадрат.
1.2.2.Деление на 8 равных частей(рис.4б).

Разделите полученные 4 дуги пополам, проведя циркулем засечки радиусом 20-30 мм из концов этих дуг. Соединяя точки пересечения засечек с центром окружности,, вы разделите окружность на 8 равных частей. Соедините полученные 8 точек, получите вписанный восьмиугольник.
1.2.З.Деление на 3 равные части (рис.4 в).

Радиусом 20мм проведите дугу с центром в точке D. Засеките на окружности точки 1 и 2 и соедините их с точкой С.

1.2.4.Деление на 6 равных частей (рис.4 г).

Приняв за центры концы диаметра, сделайте циркулем радиусом 20мм засечки на окружности (точки 1,2,3,4). Соедините их и точки А и В , получите правильный шестиугольник.

1.2.5.Деление на 12 равных частей (рис.4 д.)

Приняв за центры концы двух взаимно перпендикулярных диаметров (точки А,В,С,Д)), сделайте радиусом 20мм 8 засечек на окружности. Полученные 12 точек соедините.

Рис.4

1.2.6. Деление на 7 равных частей (рис.4 е).

Приняв за центр один из концов диаметра (точку С), проведите дугу радиусом 20 мм до пересечения с окружностью. Точки пересечения соедините отрезком прямой . Половина этого отрезка (EF) примерно равна стороне вписанного семиугольника. Радиусом FE сделайте поочередно 7 засечек на окружности, начав с точки С. Полученные 7 точек соедините.

1.2.7.Деление на 5 равных частей (рис.4 ж).

Приняв за центр один из концов диаметра (точку В), проведите дугу радиусом 20мм до пересечения с окружностью и точки пересечения соедините прямой. Приняв за центр точку пересечения прямой с :горизонтальным диаметром (точку Е), проведите дугу через точку С до пересечения с этим диаметром. Точку пересечения F соедините с точкой С. Отрезок СF будет примерно равен стороне вписанного пятиугольника ; ОF — стороне вписанного десятиугольника. Радиусом СF поочередно сделайте 5 засечек на окружности, начиная с точки С. Полученные 5 точек соедините.

1.2.8.Деление на 10 равных частей (рис.4з).

Радиусом ОF сделайте поочередно 10 засечек на окружности, полученные точки соедините.

СОПРЯЖЕНИЯ

1.3.1.Сопряжение двух прямых (рис.5.)

Даны две параллельные прямые АВ и СD (рис 5 в) , задан размер EF .Разделите отрезок EF пополам, и из точки О проведите дугу радиусом R=EF/2, соединяя точки Е и F

1.3.2.Сопряжения углов (рис.5 а, б).

Даны две прямые , пересекающиеся под углом ( прямым, острым или тупым), и радиус сопряжения Е..

Проведите по два перпендикуляра к двум сторонам углаи отложите на них отрезки ,равные R.. Через полученные точки проведите прямые параллельно сторонам угла.. О — точка пересечения этих двух прямых -есть центр сопряжения. Из точки О опустите перпендикуляры на стороны угла. Точки пересечения перпендикуляров и сторон угла соедините дугой радиусом R с центром в точке О.

1.3.3.Сопряжение прямой сокружностью (рис.6а.) Дана прямая, окружность радиусом R и радиус сопряжения R1.. Проведите прямую, параллельную заданной , на расстоянии R1. Из центра окружности О радиусом R2= R + R1 сделайте на прямой засечку О1 . Через О и О1 проведите прямую, получите на окружности точку К. Из точки О1 проведите О1К1 перпендикулярно заданной прямой. Из центра сопряжения О1 проведите дугу радиусом R1, соединяя точки К1 и К. Это внешнее сопряжение

Внутреннее сопряжение. (рис.6 б).

Дана прямая, окружность радиусом R и радиус сопряжения R1.. Проведите построение аналогично предыдущему, учитывая , что в данном случае

1.3.4.Сопряжение двух окружностей.

Внешнее сопряжение (рис.7а).

Даны две окружности радиусом R1, и R2 и радиус сопряжения R.

Проведите дуги из центра О1 радиусом R.+ R 1 , из О₂ — радиусом R.+ R 2. Точка их пересечения О3 -центр сопряжения.

Внутреннее сопряжение(рис.7б)

Даны две окружности радиусом R1и R2 и радиус сопряжения R. Проведите дуги : из точки О1 радиусом R- R1, из точки О2 радиусом R-R2. Точка их пересечения О3 -центр сопряжения.

Смешанное сопряжение (рис.7 в).

Даны две окружности радиусом R1 и R2,ирадиус сопряжения R.

Проведите дуги : из центра О1 радиусом R.-R1, из центра О2 радиусом R+R2. Точка пересечения дуг О3- центр сопряжения.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Обозначение конусности на чертежах гост

Конус – лат. conus – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.

На чертежах с коническими поверхностями иногда указывается конусность c размерными числами в виде соотношения, перед которыми устанавливается знак в виде остроугольного треугольника « ». Знак конусности с размерными числами наносятся над осевой линией или на полке линии-выноски.

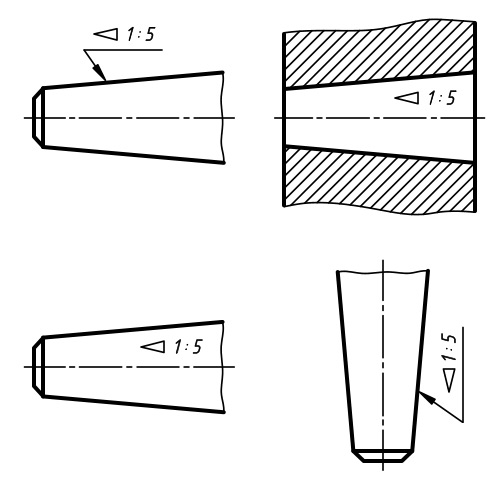
Обозначение конусности на чертежах

Отношение диаметра основания конуса к его высоте называется конусностью.

Конусность определяется по следующей формуле:

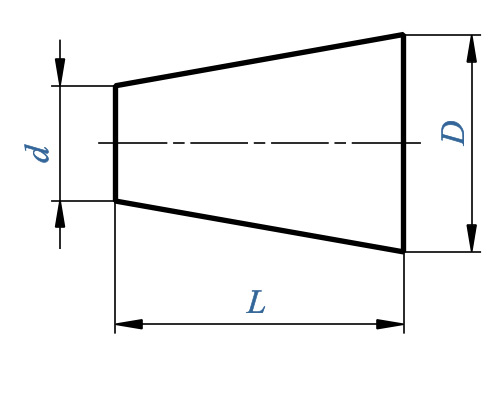
Например, если известны размеры D = 30 мм , d = 20 мм и L = 70 мм , то

Если известны конусность С , диаметр одного из оснований конуса d и длина конуса L , можно определить второй диаметр конуса. Например, С = 1:7 , d = 20 мм и L = 70 мм

Конусность – это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (рис. 1.4)

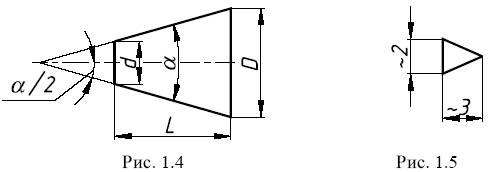
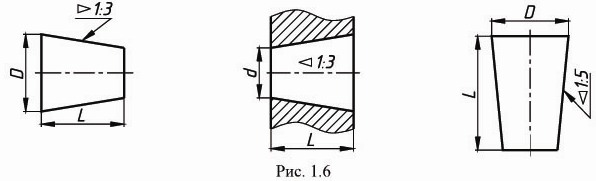
Для обозначения конусности на чертеже применяется знак (рис. 1.5) по ГОСТ 2.304-81 (размеры знака даны для шрифта № 5). Знак наносится перед размерным числом, характеризующим конусность, острый угол знака должен быть направлен в сторону вершины конуса (рис. 1.6).

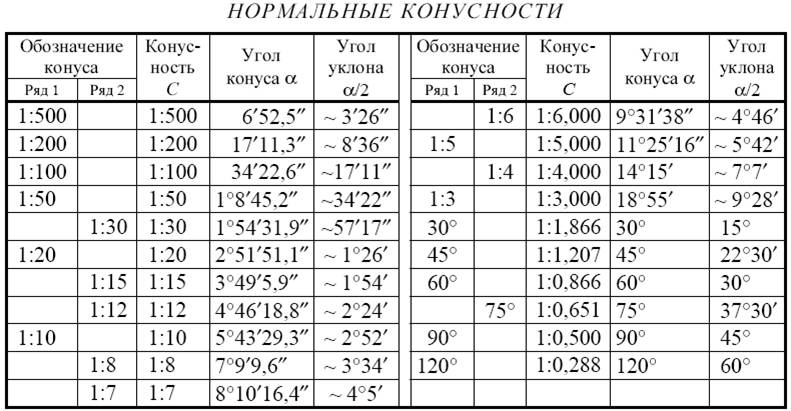
Примечание . Ряд 1 следует предпочитать ряду 2.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ПО ИНЖЕНЕРНОЙ ГРАФИКЕ

Графическая работа №3

сформировать у студентов навыки выполнения чертежей предметов с использованием геометрических построений.

чертежная бумага формата А3 (297х420), карандаши различной мягкости, набор чертежных инструментов (циркуль, измеритель, линейка, угольник, транспортир и т. п.), задание.

[1] Боголюбов С.К. Инженерная графика – М.: Машиностроение, 2009

[2] Боголюбов С.К. Индивидуальные задания по курсу черчения – М.: Высшая школа, 2009

Задание по теме: «Геометрические построения» включает в себя следующие графические задачи:

задача №1. построение профиля проката, содержащего уклон;

задача №2. изображение детали с элементами конусности;

задача №3. построение синусоиды.

Графическая работа выполняется на листе формата А3 (297 х 420 мм).

Лист содержит рамку, ограничиваю­щую поле чертежа, и основную надпись по ГОСТ 2.104-68. В за­висимости от размеров, указанных в задании, выбирается мас­штаб чертежа. При этом допускается применять 2 масштаба — один указывается в основной надписи, второй — над изображени­ем детали.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Теоретическая часть

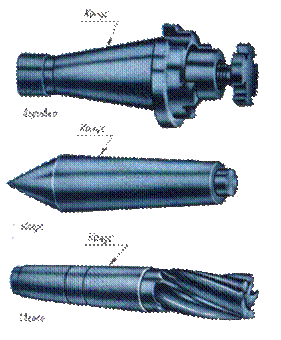
При изготовлении профилей прокатной стали, боковые полки выполняют так, что плоскости, ограничивающие их, не параллельны, а расположены под некоторым углом между собой.

В технике часто применяются конические детали. При вычерчивании чертежей многих деталей приходится выполнять ряд геометрических построений, и в этой связи рассмотрим следующие понятия: уклоны и конусность.

УКЛОН ГОСТ 8908-81

Прямые наклонные элементы, расположенные под углом относительно базовой линии создают уклон, для отображения которого перед размерными числами наносят знак « > », причём его острый угол должен быть направлен в сторону уклона. Обозначения наносятся в непосредственной близости к наклонной линии или на полке линии-выноски.

Размерные числа уклона выражаются в отношении чисел, или в процентах.

Уклон i отрезка ВС относительно отрезка ВА определяют отношением катетов прямоугольного треугольника ABC.

Для построения прямой ВС с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки A влево отложить отрезок AВ, равный четырем единицам длины, а вверх — отрезок АС, равный одной единице длины. Точки С и В соединяют прямой, которая дает направление искомого уклона.

Если уклон задается в процентах, например, 20 %, то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100 %, а другого – 20 %. Очевидно, что уклон 20 % есть иначе уклон 1:5.

КОНУСНОСТЬ ГОСТ 2.307-68

Конусность — это отношение диаметра D основания конуса к его высоте L. K=D/L

Для конуса это отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними.

Конусность равна удвоенному уклону образующей конуса к его оси. Так же как и уклон, она обозначается условным знаком, проставляемым перед её числовым обозначением. Условный знак изображается в виде треугольника с вершиной, направленной в сторону вершины конуса. Конусность задается на чертежах отношением двух чисел, процентами или десятичной дробью.

Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно оси конического элемента. Они могут быть расположены над осью или полке, как на. В последнем случае полка соединяется с образующей конуса с помощью линии-выноски, заканчивающейся стрелкой. В конических соединениях, указание конусности обязательно, так как задание размеров D, d, H из-за трудностей изготовления применяют редко. При построении очертаний конуса, задаваемого конусностью, высотой и одним из диаметров, второй диаметр вычисляют по формуле. Конусности общего назначения стандартизованы ГОСТ 8593-81.

Последовательность выполнения графической работы:

Для выполнения этой работы необходимо изучить основные положения ГОСТ 2.301, ГОСТ 2.304 — 2.307, данные в сборниках стандар­тов ЕСКД и рекомендуемой литературе, ознакомиться с примером выполнения чертежа, изучить рекомендации по выполнению чертежей и методические указания к данной теме. Приступить к выполнению графической работы Построение очертаний пробки и двутавра позволяет получить навыки в проведении линий, построении сопряжений, уклонов, конусностей, нанесении размеров, написании текста.

Порядок выполнения листа:

1. определить задание согласно своему варианту;

2. выбрать масштаб;

3. формат А3 расположить горизонтально;

4. выполнить внутреннюю рамку и основную надпись;

5. внимательно изучитьгеометрические фигуры, подлежащие вычерчиванию и выполнить разметку листа, определив место для изображения каждой задачи;

6. разметить на листе габаритные рамки двух деталей и положение осевых и центровых линий локальной кривой;

7. выполнить построения каждого изображения в тонких линиях по заданным параметрам;

8. проверить построения;

9. выполнить обводку чертежа, рамки и граф основной надписи, сохранив все вспомогательные линии;

10. провести выноски и размерные линии, нанести размеры;

11.Подписать изображения и указать при необходимости их масштаб, заполнить основную надпись.

При работе особое внимание следует уделить аккуратно­сти и точности геометрических построений!

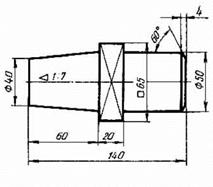Пример выполненного задания

Обозначение уклона

Кнопка Обозначение уклона — вызывает инструмент СПДС GraphiCS для отрисовки и вставки на чертеж обозначения уклона, как на разрезе, так и на плане.

Для вызова инструмента Обозначение уклона можно воспользоваться следующими способами:

• кликнуть по иконке на вкладке СПДС — панель Обозначения;
• кликнуть по иконке на панели Обозначения;
• Строка меню — СПДС — Обозначения — Обозначение уклона;
• ввести в командную строку команду spgrad.

Для отрисовки и вставки обозначения уклона необходимо:

• активировать функцию (нажать на пиктограмму или ввести в командную строку команду);
• выбрать на чертеже линию, для которой нужно проставить уклон;
• разместить обозначение уклона на выбранной линии или на полке-выноске; или
• диалоговое окно настройки обозначения становиться доступным по команде Р-свойства контекстного меню.

В диалоговом окне Уклон настройте вид обозначения:

1. Укажите вид обозначения — уклон или конусность.
2. При необходимости отключите режим ассоциативной связи, выключив кнопку (при простановке режим ассоциативности включается автоматически). Укажите в поле ввода значение уклона или конусности.
3. Выберите из выпадающего списка способ представления единиц измерения уклона:
   • как есть
   • отношение
   • десятичный
   • процент
   • промилле
   • градус
4. Укажите тип уклона:
   • на разрезе
   • на плане

По умолчанию в свойствах команды включен признак ассоциативности. На рисунке ниже показан перенос конечной точки отрезка. Значение уклона обновилось автоматически.

При отключении ассоциативности становиться доступной кнопка Измерить уклон, с помощью которой можно замерить значение уклона на экране.

Обозначение уклона можно настроить самому, перейдя в настройки программы:

Редактирование обозначения уклона осуществляется следующими способами:

• два раза кликнуть левой кнопкой мышки по обозначению;
• кликнуть правой кнопкой мышки по обозначению;
• выделить обозначение и кликнув правой кнопкой мышки вызвать контекстное меню, в котором выбрать пункт Редактировать;
• активировать функцию Редактирование и указать на обозначение;
• воспользоваться окном Свойства AutoCAD;
• с помощью ручек редактирования.

В данном уроке Вы узнали об инструменте СПДС GraphiCS, с помощью которого всего в несколько кликов можно нарисовать Обозначение уклона. Данный инструмент поможет Вам ускорить процесс выполнения чертежей.

Техническое черчение

Popular

Основы черчения

Строительное

Машиностроительное

Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:

i=AC/AB=tga

Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)

k=(D-d)/l=2tga

k = 2i

Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.

Например: конусность, выраженная в градусах — 11°25’16»; отношением — 1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38»; отношением — 1:10; дробью—0,1; в процентах — 10%.

Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.

Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):

1) построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2) опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм. Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2. В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:

ps/np=10/100,

ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

i=ps/np=1/6

где i — заданный уклон.

Подставив в формулу числовые значения, получим

ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.